转移函数的分子、分母多项式可以分别做因式分解,得:
H ( z ) = g z N − M ∏ r = 1 M ( z − z r ) ∏ r = 1 N ( z − p k ) H(z) = g z^{N-M}\frac{\prod_{r=1}^M(z-z_r)}{\prod_{r=1}^N(z-p_k)}
H ( z ) = g z N − M ∏ r = 1 N ( z − p k ) ∏ r = 1 M ( z − z r )
式中g为系统的增益因子
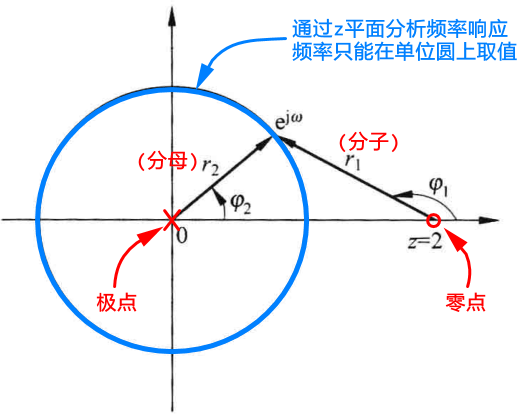
将上式H ( z ) H(z) H ( z ) 极点和零点 画在z平面上得到的图形可称为极零图
若要通过极零图 判断系统的频率响应,则必须在z平面上的单位圆 上取值,即令z = e j w z = e^{jw} z = e j w
H ( e j w ) = g e j ( N − M ) w ∏ r = 1 M ( e j w − z r ) ∏ r = 1 N ( e j w − p k ) H(e^{jw}) = g e^{j(N-M)w}\frac{\prod_{r=1}^M(e^{jw}-z_r)}{\prod_{r=1}^N(e^{jw}-p_k)}
H ( e j w ) = g e j ( N − M ) w ∏ r = 1 N ( e j w − p k ) ∏ r = 1 M ( e j w − z r )
系统幅频响应:
∣ H ( e j w ) ∣ = g ∏ r = 1 M ∣ e j w − z r ∣ ∏ r = 1 N ∣ e j w − p k ∣ |H(e^{jw})| = g \frac{\prod_{r=1}^M|e^{jw}-z_r|}{\prod_{r=1}^N|e^{jw}-p_k|}
∣ H ( e j w ) ∣ = g ∏ r = 1 N ∣ e j w − p k ∣ ∏ r = 1 M ∣ e j w − z r ∣
系统相频响应:
φ ( e W ) = arg [ e ( N − M ) α ] + ∑ r = 1 M [ arg ( e i ω − z r ) ] − ∑ k = 1 N [ arg ( e W − p k ) ] \varphi\left(\mathrm{e}^{\mathrm{W}}\right)=\arg \left[\mathrm{e}^{(N-M) \alpha}\right]+\sum_{r=1}^{M}\left[\arg \left(\mathrm{e}^{\mathrm{i} \omega}-z_{r}\right)\right]-\sum_{k=1}^{N}\left[\arg \left(\mathrm{e}^{\mathrm{W}}-p_{k}\right)\right]
φ ( e W ) = arg [ e ( N − M ) α ] + r = 1 ∑ M [ arg ( e i ω − z r ) ] − k = 1 ∑ N [ arg ( e W − p k ) ]
例题 :一个LSI系统的差分方程是
y ( n ) = x ( n ) − 4 x ( n − 1 ) + 4 x ( n − 2 ) y(n) = x(n) - 4x(n-1) + 4x(n-2)
y ( n ) = x ( n ) − 4 x ( n − 1 ) + 4 x ( n − 2 )
试用极零分析画出该系统的幅频响应 及相频相应 。
将差分方程进行Z Z Z 转移函数 :
H ( z ) = 1 − 4 z − 1 + 4 z − 2 = z 2 − 4 z + 4 z 2 = ( z − 2 ) 2 z 2 H(z) = 1 - 4z^{-1} + 4z^{-2} =\frac{z^2-4z+4}{z^2} = \frac{(z-2)^2}{z^2}
H ( z ) = 1 − 4 z − 1 + 4 z − 2 = z 2 z 2 − 4 z + 4 = z 2 ( z − 2 ) 2
首先该系统是F I R FIR F I R z = 2 z=2 z = 2 z = 0 z=0 z = 0
系统的幅频响应 :
∣ H ( e j w ) ∣ = ∣ e j w − 2 ∣ 2 ∣ e j w − 0 ∣ 2 = ∣ e j w − 2 ∣ 2 1 = r 1 2 r 2 2 |H(e^{jw})| = \frac{|e^{jw}-2|^2}{|e^{jw}-0|^2}=\frac{|e^{jw}-2|^2}{1}=\frac{r_1^2}{r_2^2}
∣ H ( e j w ) ∣ = ∣ e j w − 0 ∣ 2 ∣ e j w − 2 ∣ 2 = 1 ∣ e j w − 2 ∣ 2 = r 2 2 r 1 2
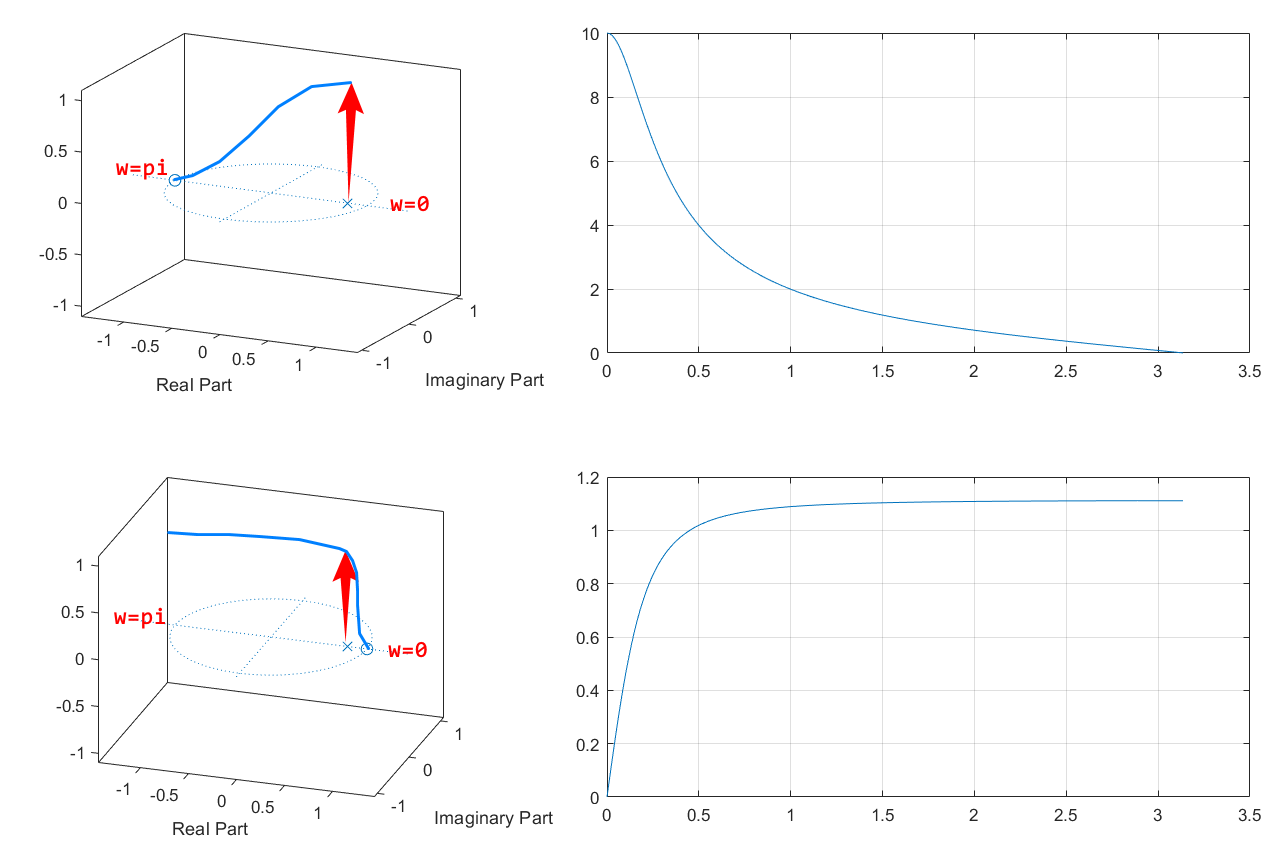
幅频响应分析:
当w = 0 w=0 w = 0 r 1 = r 2 = 1 r_1=r_2=1 r 1 = r 2 = 1 ∣ H ( e j 0 ) ∣ = 1 |H(e^{j0})|=1 ∣ H ( e j 0 ) ∣ = 1
当w w w π \pi π r 1 > r 2 r_1>r_2 r 1 > r 2 ∣ H ( e j 0 ) ∣ |H(e^{j0})| ∣ H ( e j 0 ) ∣
当w = π w=\pi w = π r 1 = 3 , r 2 = 1 r_1=3,r_2=1 r 1 = 3 , r 2 = 1 ∣ H ( e j w ) = 9 ∣ |H(e^{jw})=9| ∣ H ( e j w ) = 9 ∣
由w w w π \pi π 2 π 2\pi 2 π ∣ H ( e j w ) ∣ |H(e^{jw})| ∣ H ( e j w ) ∣
分配原则:
具体分配实例课件例题 2.5.4:
例题 2.5.4
H 0 ( z ) = a 1 + z − 1 1 − p z − 1 H 1 ( z ) = b 1 − z − 1 1 − p z − 1 H 2 ( z ) = c ( 1 + z − 1 ) ( 1 − z − 1 ) ( 1 − r e i α z − 1 ) ( 1 − r e − i ω z − 1 ) \begin{array}{l}
H_{0}(z)=a \frac{1+z^{-1}}{1-p z^{-1}} \\
H_{1}(z)=b \frac{1-z^{-1}}{1-p z^{-1}} \\
H_{2}(z)=c \frac{\left(1+z^{-1}\right)\left(1-z^{-1}\right)}{\left(1-r \mathrm{e}^{\mathrm{i} \alpha} z^{-1}\right)\left(1-\mathrm{re}^{-\mathrm{i} \omega} z^{-1}\right)}
\end{array}
H 0 ( z ) = a 1 − p z − 1 1 + z − 1 H 1 ( z ) = b 1 − p z − 1 1 − z − 1 H 2 ( z ) = c ( 1 − r e i α z − 1 ) ( 1 − r e − i ω z − 1 ) ( 1 + z − 1 ) ( 1 − z − 1 )
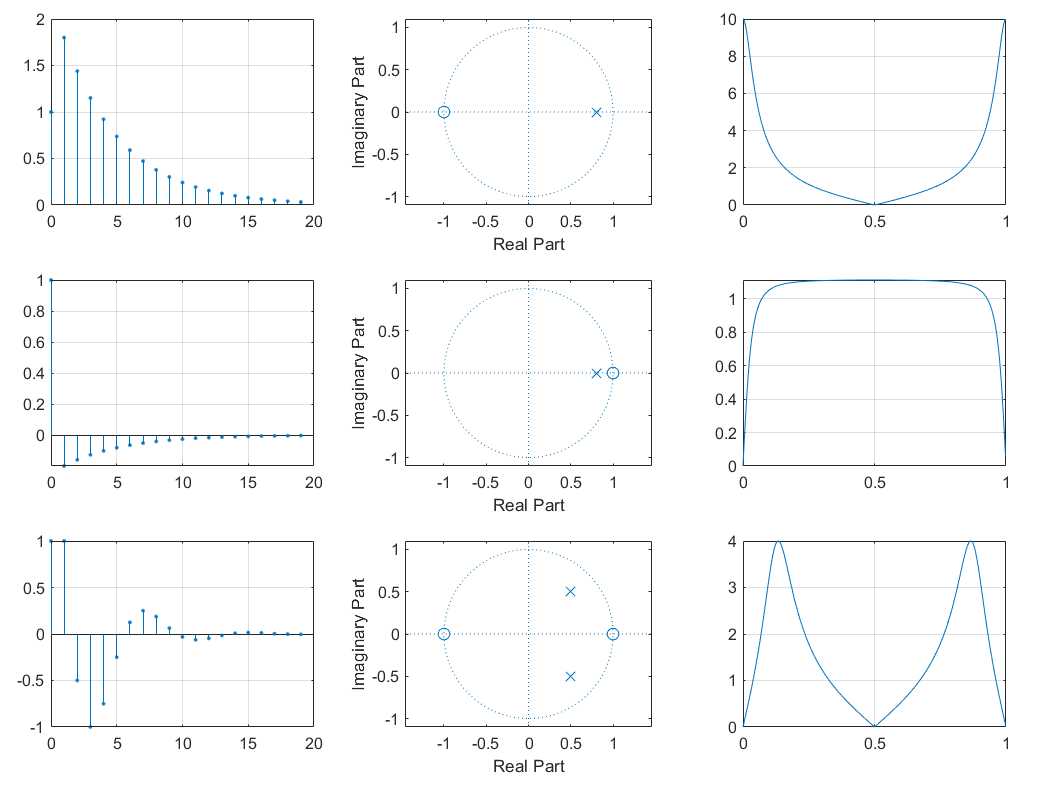
其幅频响应 ,极零点分布状况 ,单位冲击响应 为:
其中,系数a , b , c a,b,c a , b , c
Matlab代码:
b_1 = [1 ,1 ];a_1 = [1 ,-0.8 ]; b_2 = [1 ,-1 ];a_2 = [1 ,-0.8 ]; z = [-1 ,1 ]';p = [0.5 +0.5 i ,0.5 -0.5 i ]'; [b_3,a_3] = zp2tf(z,p,1 ); [h_1,t_1] = impz(b_1,a_1,20 ); [H_1,w_1] = freqz(b_1,a_1,512 ,'whole' ,1 );Hr_1 = abs (H_1); [h_2,t_2] = impz(b_2,a_2,20 ); [H_2,w_2] = freqz(b_2,a_2,512 ,'whole' ,1 );Hr_2 = abs (H_2); subplot 331 ;stem(t_1,h_1,'.' );grid on; subplot 332 ;zplane(b_1,a_1); subplot 333 ;plot (w_1,Hr_1);grid on; subplot 334 ;stem(t_2,h_2,'.' );grid on; subplot 335 ;zplane(b_2,a_2); subplot 336 ;plot (w_2,Hr_2);grid on; [h_3,t_3] = impz(b_3,a_3,20 ); [H_3,w_3] = freqz(b_3,a_3,512 ,'whole' ,1 );Hr_3 = abs (H_3); subplot 337 ;stem(t_3,h_3,'.' );grid on; subplot 338 ;zplane(b_3,a_3); subplot 339 ;plot (w_3,Hr_3);grid on; set(gcf,'color' ,'w' )
系统可以通过转移函数来定义:
H ( z ) = B ( z ) A ( z ) = b ( 1 ) + b ( 2 ) z − 1 + b ( 3 ) z − 2 + ⋯ + b ( n b + 1 ) z − n b 1 + a ( 2 ) z − 1 + a ( 3 ) z − 2 + ⋯ + a ( n a + 1 ) z − n a H(z) = \frac{B(z)}{A(z)} = \frac{b(1)+b(2)z^{-1}+b(3)z^{-2}+\dots+b(n_b+1)z^{-n_b}}{1+a(2)z^{-1}+a(3)z^{-2}+\cdots+a(n_a+1)z^{-n_a}}
H ( z ) = A ( z ) B ( z ) = 1 + a ( 2 ) z − 1 + a ( 3 ) z − 2 + ⋯ + a ( n a + 1 ) z − n a b ( 1 ) + b ( 2 ) z − 1 + b ( 3 ) z − 2 + ⋯ + b ( n b + 1 ) z − n b
分子和分母的系数为:
b = [ b ( 1 ) , b ( 2 ) , … , b ( n b + 1 ) ] a = [ a ( 1 ) , a ( 2 ) , … , a ( n b + 1 ) ] b = [b(1),b(2),\dots,b(n_b+1)]\\
a = [a(1),a(2),\dots,a(n_b+1)]
b = [ b ( 1 ) , b ( 2 ) , … , b ( n b + 1 ) ] a = [ a ( 1 ) , a ( 2 ) , … , a ( n b + 1 ) ]
filter.m本文件可以根据转移函数系数求一个离散系统的**时域输出。**即,
y ( n ) = x ( n ) ∗ h ( n ) y(n) = x(n) * h(n)
y ( n ) = x ( n ) ∗ h ( n )
上式中,h ( n ) h(n) h ( n ) a a a b b b
y ( n ) = b ( 1 ) x ( n ) + b ( 2 ) x ( n − 1 ) + ⋯ + b ( n b + 1 ) x ( n − n b ) − a ( 2 ) y ( n − 1 ) − ⋯ − a ( n a + 1 ) y ( n − n a ) \begin{aligned}
y(n)=& b(1) x(n)+b(2) x(n-1)+\cdots+b\left(n_{b}+1\right) x\left(n-n_{b}\right) \\
&-a(2) y(n-1)-\cdots-a\left(n_{a}+1\right) y\left(n-n_{a}\right)
\end{aligned}
y ( n ) = b ( 1 ) x ( n ) + b ( 2 ) x ( n − 1 ) + ⋯ + b ( n b + 1 ) x ( n − n b ) − a ( 2 ) y ( n − 1 ) − ⋯ − a ( n a + 1 ) y ( n − n a )
调用格式:y=filter(b,a,x)
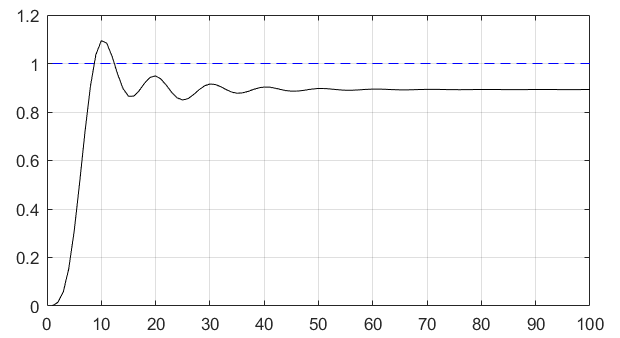
**例题:**求系统的阶跃相应(所谓阶跃响应是系统对阶跃输入的输出)
H ( z ) = 0.001836 + 0.007344 z − 1 + 0.011016 z − 2 + 0.007374 z − 3 + 0.001836 z − 4 1 − 3.0544 z − 1 + 3.8291 z − 2 − 2.2925 z − 3 + 0.55075 z − 4 H(z)=\frac{0.001836+0.007344 z^{-1}+0.011016 z^{-2}+0.007374 z^{-3}+0.001836 z^{-4}}{1-3.0544 z^{-1}+3.8291 z^{-2}-2.2925 z^{-3}+0.55075 z^{-4}}
H ( z ) = 1 − 3 . 0 5 4 4 z − 1 + 3 . 8 2 9 1 z − 2 − 2 . 2 9 2 5 z − 3 + 0 . 5 5 0 7 5 z − 4 0 . 0 0 1 8 3 6 + 0 . 0 0 7 3 4 4 z − 1 + 0 . 0 1 1 0 1 6 z − 2 + 0 . 0 0 7 3 7 4 z − 3 + 0 . 0 0 1 8 3 6 z − 4
Matlab代码:
x = ones(100);t = 1:100; b = [.001836,.007344,.011016,.0073774,.001836]; a = [1,-3.0544,3.8291,-2.2925,.55075]; y = filter(b,a,x); plot(t,x,'b--',t,y,'k-');grid on; set(gcf,'color','w');
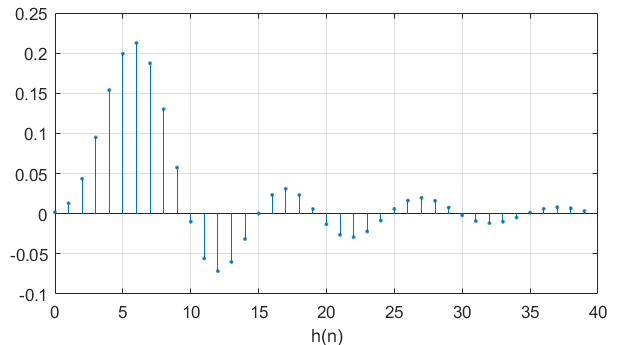
impz.m本文件可以用来求出系统的单位抽样响应h ( n ) h(n) h ( n )
调用格式:[h,t]=impz(b,a,N)
Matlab编程:
[h,t] = impz(b,a,40 );stem(t,h,'.' );grid on; set(gcf,'color' ,'w' );
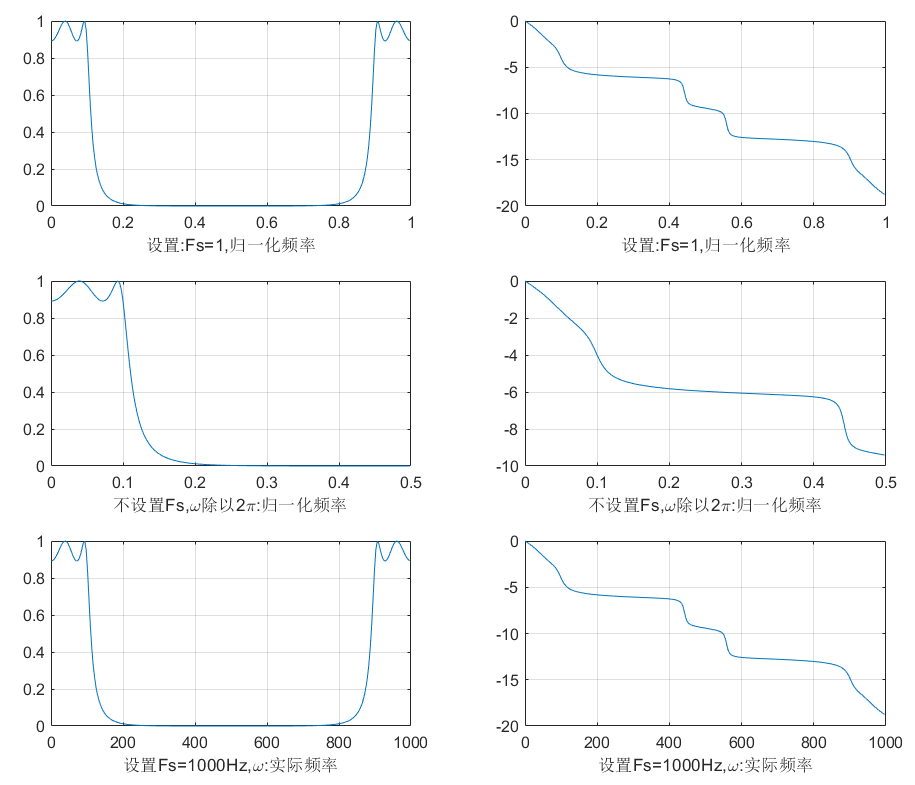
freqz.m根据系数a和b,求出系统的幅频响应 H ( e j w ) H(e^{jw}) H ( e j w )
调用格式:[H,w]=freqz(b,a,N,'whole',Fs)
其中,N是频率轴的分点数,建议为2的幂;w是返回频率轴坐标向量 ;若Fs=1,频率轴给出归一化频率 ;whole指定计算的频率范围是0 ∼ F s 0 \sim Fs 0 ∼ F s 0 ∼ F s / 2 0 \sim Fs/2 0 ∼ F s / 2
三种调用格式:
Matlab代码:
[H,w] = freqz(b,a,256 ,'whole' ,1 ); Hr = abs (H); Hphase = angle (H);Hphase = unwrap (Hphase); subplot 321 ;plot (w,Hr);grid on;xlabel('设置:Fs=1,归一化频率' ) subplot 322 ;plot (w,Hphase);grid on; xlabel('设置:Fs=1,归一化频率' ) [H,w] = freqz(b,a,256 ); Hr = abs (H); Hphase = angle (H);Hphase = unwrap (Hphase); subplot 323 ;plot (w/(2 *pi ),Hr);grid on;xlabel('不设置Fs,\omega除以2\pi:归一化频率' );xlim([0 ,0.5 ]); subplot 324 ;plot (w/(2 *pi ),Hphase);grid on;xlabel('不设置Fs,\omega除以2\pi:归一化频率' );xlim([0 ,0.5 ]); set(gcf,'color' ,'w' ); [H,w] = freqz(b,a,256 ,'whole' ,1000 ); Hr = abs (H); Hphase = angle (H);Hphase = unwrap (Hphase); subplot 325 ;plot (w,Hr);grid on;xlabel('设置Fs=1000Hz,\omega:实际频率' ) subplot 326 ;plot (w,Hphase);grid on;xlabel('设置Fs=1000Hz,\omega:实际频率' ) set(gcf,'color' ,'w' );
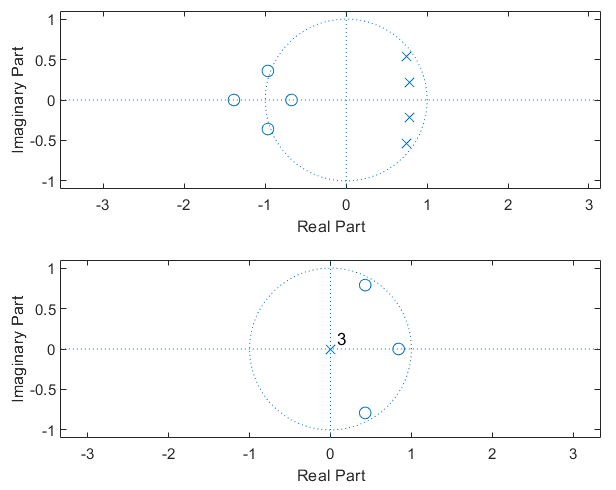
zplane.m调用格式: zplane(z,p) 以及 zplane(b,a)
例如:求FIR系统的极零图
H ( z ) = 1 − 1.7 z − 1 + 1.53 z − 2 − 0.648 z − 3 H(z) = 1 -1.7z^{-1}+1.53z^{-2} - 0.648z^{-3}
H ( z ) = 1 − 1 . 7 z − 1 + 1 . 5 3 z − 2 − 0 . 6 4 8 z − 3
Matlab编程:
b = [.001836 ,.007344 ,.011016 ,.007374 ,.001836 ]; a = [1 ,-3.0544 ,3.8291 ,-2.2925 ,.55075 ]; subplot 211 ;zplane(b,a); b = [1 ,-1.7 ,1.53 ,-0.68 ]; a = 1 ; subplot 212 ;zplane(b,a); set(gcf,'color' ,'w' )
zp2tf.m已知零极点 z z z p p p 系数 a a a b b b
Matlab编程:
z = [-1 ,1 ]';p = [0.5 +0.5 i ,0.5 -0.5 i ]'; [b_3,a_3] = zp2tf(z,p,1 ); [h_3,t_3] = impz(b_3,a_3,20 ); [H_3,w_3] = freqz(b_3,a_3,512 ,'whole' ,1 );Hr_3 = abs (H_3); subplot 331 ;stem(t_3,h_3,'.' );grid on;xlabel('h(n)' ) subplot 332 ;zplane(b_3,a_3); subplot 333 ;plot (w_3,Hr_3);grid on;xlabel('幅频图' ) set(gcf,'color' ,'w' )