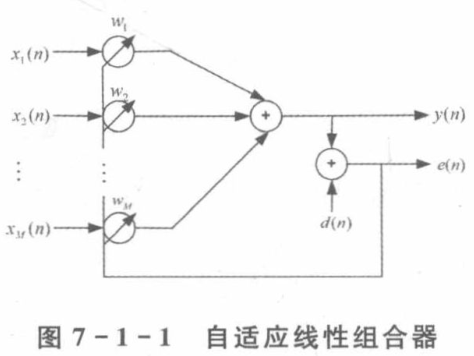
自适应滤波器减噪
0. 前言知识
什么是自适应滤波?
自适应滤波:根据前一时刻的序列,自动的调节这一时刻的滤波器参数。
实质:一种能调节自身传输特性以达到最优的维纳滤波器。
几种自适应滤波器的比较
- 自适应:无需信号的先验知识,适用于实时处理。
- 维纳滤波:参数固定,适用于平稳随机信号。
- 卡尔曼滤波器:参数时变,适合于非平稳随机信号。
常用滤波器算法
- LMS(最小均方)自适应滤波器
- RLS(递推最小二乘)滤波器
- IIR(无限冲激相应)滤波器
应用分类:
1. LMS滤波
LMS原理及推导
X(n)=[x(n),x(n−1),…,x(n−L)]是一截输入信号序列,d(n)为期望输出信号,两者之差定义为误差序列:
e(n)=d(n)−i=1∑Lwix(n−i)
LMS中滤波器的权系数则为:wi
注:有的博客或者书中权重系数都是wi(n)代表权重是动态变化的。
![]()
用矩阵表达:
e(n)=d(n)−WTX(n)
误差二次方为:
e2(n)=d2(n)−2d(n)XT(n)W+WTX(n)XT(n)W
自适应线性组合器按照误差信号均方值最小的准则,即
E[e2(n)]=E[d2(n)]−2E[d(n)XT(n)]W+WTE[X(n)XT(n)]W
定义自相关矩阵R和互相关矩阵P
R=P=E[X(n)XT(n)]E[d(n)XT(n)]
则有:
E[e2(n)]=E[d2(n)]+WTRW−2PTW
在d(n)和X(n)都是平稳随机信号的情况下,均方误差是权矢量(W,由L+1个权系数wi构成)的各分量的二次函数。该曲面是一个L+2维空间的上凸下凹的超抛物面。(这还需待补充,画张图)
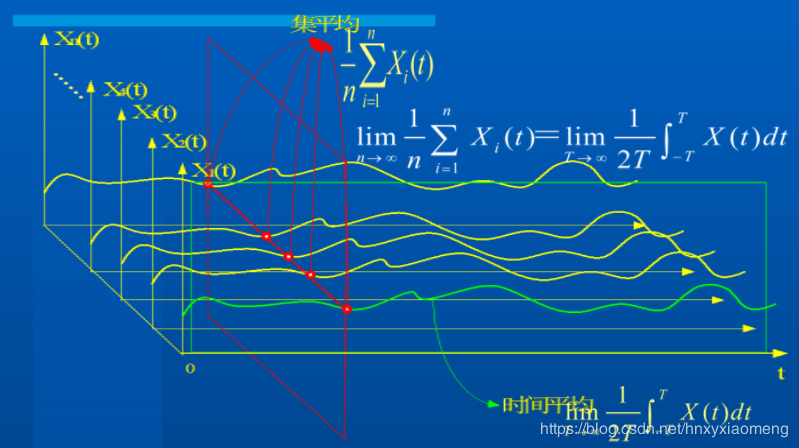
这里还需要补充随机信号的时间平均与集平均的概念
![]()
集平均就是指多次同一个随机信号多次测试取平均。根据滤波器的宽度,这里的期望就是多次平移信号取均值。
求一阶导数:
∇(n)=∂W∂E[e2(n)]=2RW−2P
令梯度等于0,可以求得最小均方误差对应的最佳权矢量W或维纳解W∗。
W∗=R−1P
最小均方(LMS)算法
若直接按照上面的公式去计算,需要精确地知道输入信号和期望信号的先验统计知识R,这就无法做到实时的滤波效果,为了避免求逆操作,这里采用迭代的方式搜索曲面的最低点。曲面最陡下降方向是负梯度方向。最陡下降法迭代计算权矢量公式为:
W(n+1)=W(n)−μ∇(n)
核心:直接用e2(n)作为均方误差E[e2(n)]的估计值,即
∇^(n)≈∇[e2(n)]=2e(n)∇[e(n)]=−2e(n)X(n)
说明:∇^(n)只是 当个平方误差序列的梯度,而∇(n)是多个平方误差序列统计平均的梯度。LMS算法就是用前者作为后者的近似,我个人理解类似用于Mini-batch版本的SGD。
最终的迭代公式为:
W(n+1)=W(n)+2μe(n)X(n)
LMS算法实践
期望信号的说明
- 准备两个麦克风,一个麦克风录制
人+噪声,另一个麦克风远离人,只录制噪声。期望信号设定为实际的信号,而输入信号则设置为猜想的噪音信号,随着迭代的过程,输入噪音信号越接近于实际信号中包含的噪音成分。最终误差序列则为减噪后的序列。
- 我们已知信号为
sin函数,但是不知道具体的幅值和相位。可以设置输入信号为sin函数,期望信号为实际的信号。可以通过LMS方法求的函数的幅值和相位。—陷波应用(去除单频噪声)
流程
- 从输入序列中x(n)中,提取出与滤波器长度相同的一段语音段x^(n)
- 将这段与权系数相乘
- 迭代误差,响应序列减去输入序列
e(n)=d(n)-y(n)
- 根据迭代公式,更新权矢量。
- ⭐️将x(n)往右平移一个数据点,重复2~5。
Matlab编程
function [yn,W,en]=LMSfilter(xn,dn,M,mu)
itr = length(xn);
en = zeros(itr,1);
W = zeros(M,itr);
for k = M:itr
x = xn(k:-1:k-M+1);
y = W(:,k-1).' * x;
en(k) = dn(k) - y ;
W(:,k) = W(:,k-1) + 2*mu*en(k)*x;
end
yn = inf * ones(size(xn));
for k = M:length(xn)
x = xn(k:-1:k-M+1);
yn(k) = W(:,end).'* x;
end
end
|
应用实例
Matlab自编函数测试
fle='C:\Users\wangj\Documents\我的坚果云\思维导图\语音识别\声纹识别代码\宋知用voice_box\speech_signal\bluesky1.wav';
[s, fs] = v_readwav(fle);
s = s-mean(s);
s = s/max(abs(s));
N = length(s);
time = (0:N-1)/fs;
noise = randn(size(s))*0.1;
M = 32 ;
mu = 0.001 ;
[yn,W,en]=LMSfilter(noise,s+noise,M,mu);
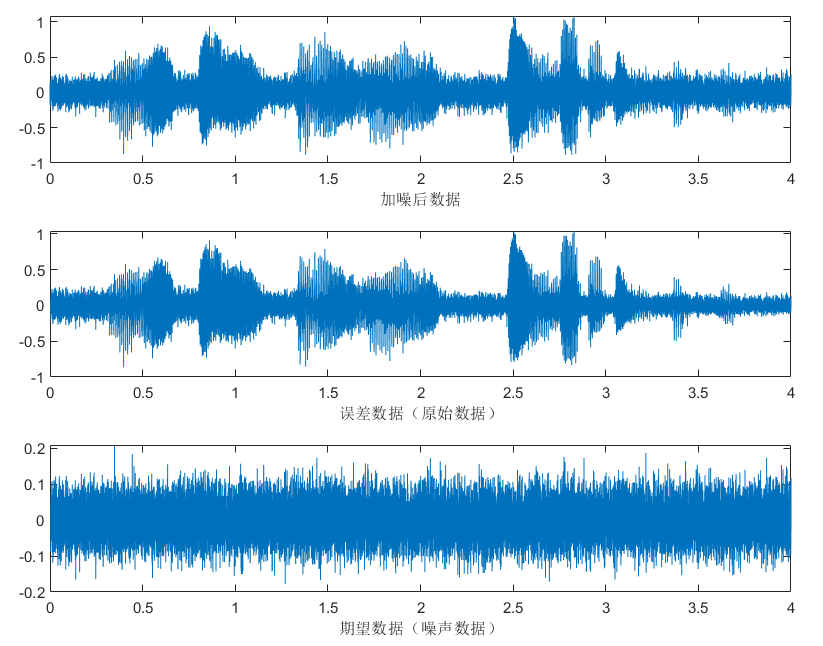
subplot(3,1,1);plot(time,s+noise);xlabel('加噪后数据')
subplot(3,1,2);plot(time,en);xlabel('误差数据(原始数据)')
subplot(3,1,3);plot(time,yn);xlabel('期望数据(噪声数据)')
set(gcf,'color','w')
|
实验结果:
![]()
可以发现,自编的算法效果并不是特别好。下面用Matlab库里面的函数再测试一下:
Matlab自带函数测试
clc;clear all;close all;
[s,Fs] = v_readwav('C:\Users\wangj\Documents\我的坚果云\思维导图\语音识别\声纹识别代码\宋知用voice_box\speech_signal\bluesky1.wav','n');
n = length(s);
t=(0:n-1);
figure(1);
subplot(4,1,1);
plot(t,s);grid;ylabel('幅度');xlabel('时间');title('原始音频信号');
noise = sqrt(0.1)*randn(n,1);
subplot(4,1,2);
plot(t,noise);grid;ylabel('幅度');xlabel('时间');title('相关噪声信号');
dn = s + noise;
subplot(4,1,3);plot(t,dn);grid;
ylabel('幅度');xlabel('时间');title('含噪音频信号d(n)');
lms = dsp.LMSFilter;
[z,elms,w] = lms(noise,s+noise);
subplot(4,1,4);plot(t,z);grid;
ylabel('幅度');xlabel('时间');title('输出序列y(n)');
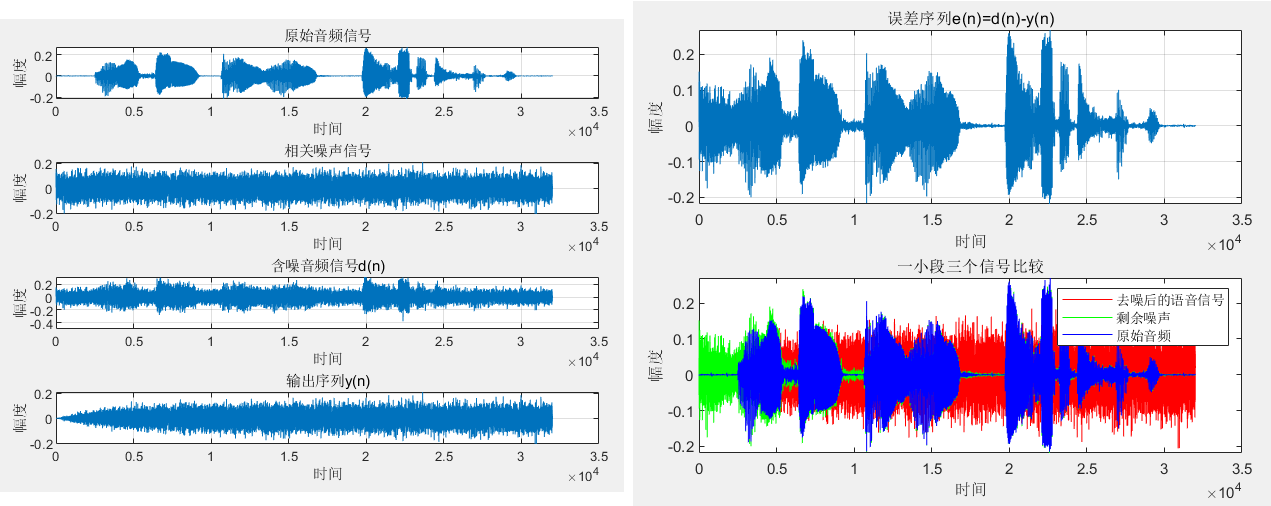
figure(2);
subplot(2,1,1);
plot(t,elms);grid;ylabel('幅度');xlabel('时间');title('误差序列e(n)=d(n)-y(n)');
subplot(2,1,2) ;
t= 1: length(z) ;
plot(t,z,'r',t,elms,'g',t,s,'b') ;ylabel('幅度');xlabel('时间');
legend('去噪后的语音信号','剩余噪声','原始音频');title('一小段三个信号比较');
|
![]()
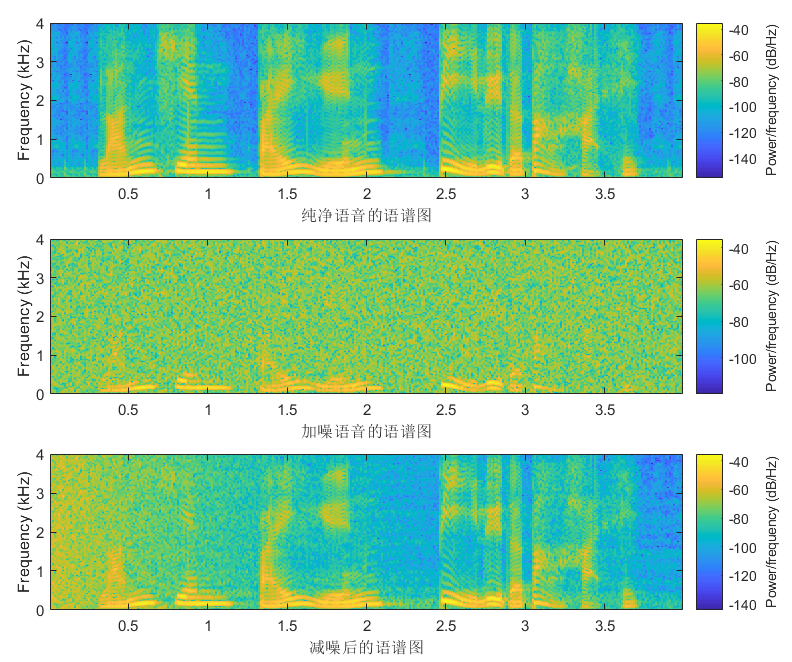
观察语谱图
可以发现打圈的地方,降噪的结果并不是很好。
figure(3);
wlen=200;
window = hanning(wlen);
inc=100;
nfft = 1024 ;
subplot(3,1,1);
spectrogram(s,window,inc,nfft,Fs,'yaxis');
xlabel('纯净语音的语谱图')
subplot(3,1,2);
spectrogram(dn,window,inc,nfft,Fs,'yaxis');
xlabel('加噪语音的语谱图')
subplot(3,1,3);
spectrogram(elms,window,inc,nfft,Fs,'yaxis');
xlabel('减噪后的语谱图')
|
![]()
以下是LMS默认的训练超参数:
lms:
Method: 'LMS'
Length: 32
StepSizeSource: 'Property'
StepSize: 0.1000
LeakageFactor: 1
InitialConditions: 0
AdaptInputPort: false
WeightsResetInputPort: false
WeightsOutput: 'Last'
|
可以通过下面的代码对超参数进行设置:
lms = dsp.LMSFilter('Length',32,'Method','LMS', ...
'StepSize',0.0001,'LeakageFactor',0.99999, ...
'WeightsOutput','All');
|
2. 归一化LMS滤波
通过LMS算法中对权矢量的迭代公式可以发现:
W(n+1)=W(n)+2μe(n)X(n)
X(n)的值影响到了权矢量的迭代量。当X(n)较大时,公式可能无法收敛。
还可以发现LMS算法中的步长为一给定的常数μ,NLMS算法中的步长为根据时间变换的量,即
μ(n)=∥X(n)∥2α
考虑到分母为0等情况,最终的NLMS的迭代公式为:
W(n+1)=W(n)+c+∥X(n)∥22μe(n)X(n)
Matlab代码中有关dsp.LMSfilter的算法说明
![]()
无论对于不相关数据还是相关数据NLMS要比标准LMS可能呈现更快的收敛速度。
NLMS 公式推导
LMS公式存在的问题:W(n+1)−W(n)这个值很飘,受很多因素的影响。现希望自适应滤波器的权向量以最小方式改变。
原先的LMS方程为:
e(n)=d(n)−WT(n)X(n)
注:这里W(n)代表第n个时刻的权重值。而非权重系数有n个!!!
按照剧本应该求误差的均方误差最小【即误差平方的2范数最小:min∥e2(n)∥】。
现在要求:
d(n)=WT(n+1)X(n)
可以发现LMS算法的方程变为:
e(n)=(WT(n+1)−WT(n))X(n)
让e(n)最小,等价于让δW(n+1)=W(n+1)−W(n) 变化最小,这里选择δW(n+1)的二范数为代价函数:
J(n)=∥δW(n+1)∥2+λ⋅(d(n)−W(n+1)X(n))
注:这里还用了拉格朗日定理。
求导等于0:
∂W(n+1)∂J(n)=2(W(n+1)−W(n))−λ⋅X(n)=0
得n+1时刻的权矢量的迭代公式:
W(n+1)=W(n)+21λ∗X(n)
进一步地,将上述代入限制条件,可以求解出λ
d(n)=W(n+1)TX(n)==W(n)TX(n)+21λ∥X(n)∥2y(n)+21λ∥X(n)∥2
进一步整理可有:
e(n)=λ=d(n)−y(n)=21λ∥X(n)∥2∥X(n)∥22e(n)
综上,可得NLMS的权矢量的迭代公式:
W(n+1)==W(n)+21∥X(n)∥22e(n)X(n)W(n)+∥X(n)∥21e(n)X(n)
增加一个控制增量变量的量μ,以及一个防止分母为0的量c(极小值),有:
W(n+1)=W(n)+c+∥X(n)∥22μe(n)X(n)
3. 自适应陷波
什么是陷波?
陷波器:对特定频率的信号有着很强的衰减的滤波器,也即阻带带宽极窄的带阻滤波器。
使用前提
我们需要知道原始信号里的干扰信号频率是多少时(例如最常见的50Hz工频干扰),这时我们只需要知道这个干扰信号的相位和幅度,然后就可以完全的“再现”这个干扰信号。
自适应陷波器
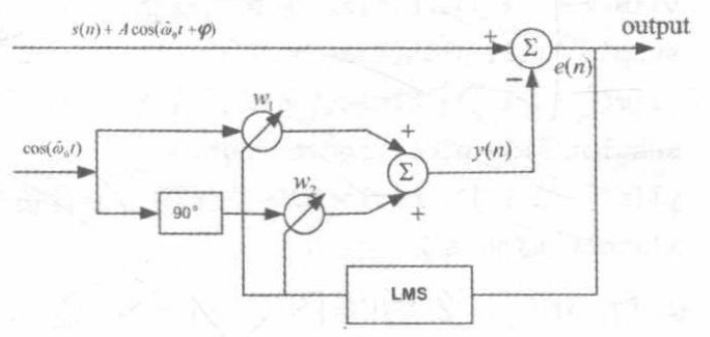
假设信号中的噪声是单色干扰(频率为ω0),则原始信号为:s(t)+Acos(ω0t+ϕ),其中Acos(ω0t+ϕ)是噪声部分。如果我们希望去除这部分的噪声,就需要知道噪声信号对应的相位和幅度。
构造输出信号 X(n)=[x1(n),x2(n)] 为:x1=cos(ω0n) 和x2=sin(ω0n)
![自适应陷波器流程示意图]()
应用实例
宋知用案例
clear all; clc; close all;
filedir=[];
filename='bluesky1.wav';
fle = [filedir filename];
[s,fs]=wavread(fle);
s=s/max(abs(s));
N=length(s);
time=(0:N-1)/fs;
ns=0.5*cos(2*pi*50*time);
x=s+ns';
x1=cos(2*pi*50*time);
x2=sin(2*pi*50*time);
w1=0.1;
w2=0.1;
e=zeros(1, N);
y=zeros(1, N);
mu=0.05;
for i=1: N
y(i)=w1 * x1(i)+ w2 * x2(i);
e(i) =x(i)-y(i);
w1=w1+mu * e(i) * x1(i);
w2=w2+mu * e(i) * x2(i);
end
output=e';
snr1=SNR_singlech(s,x);
snr2=SNR_singlech(s,output);
snr=snr2-snr1;
fprintf('snr1=%5.4f snr2=%5.4f snr=%5.4f\n',snr1,snr2,snr);
figure(1);
subplot 311; plot(time,s,'k');
ylim([-1 1 ]); title('原始语音信号');
subplot 312; plot(time,x,'k');
ylim([-1 1 ]); title('带噪语音信号');
subplot 313; plot(time,output,'k');
ylim([-1 1 ]); title('LMS滤波输出语音信号');
xlabel('时间/s')
set(gcf,'color','w')
nfft = length(s) ;
freq=linspace(0,fs/2,nfft/2+1) ;
fft_s = fft(s,nfft);
fft_x = fft(x,nfft);
fft_output = fft(output,nfft);
figure(2);
subplot 311; plot(freq,abs(fft_s(1:nfft/2+1))) ;
xlabel('原始语音信号');
subplot 312; plot(freq,abs(fft_x(1:nfft/2+1))) ;ylim([0,600])
xlabel('带噪语音信号');
subplot 313; plot(freq,abs(fft_output(1:nfft/2+1))) ;
xlabel('LMS滤波输出语音信号');
set(gcf,'color','w')
wlen=200;
window = hanning(wlen);
inc=100;
figure(3);
subplot 311; spectrogram(s,window,inc,nfft,fs,'yaxis');
xlabel('原始语音信号');
subplot 312; spectrogram(x,window,inc,nfft,fs,'yaxis');
xlabel('带噪语音信号');
subplot 313; spectrogram(output,window,inc,nfft,fs,'yaxis');
xlabel('LMS滤波输出语音信号');
set(gcf,'color','w')
|
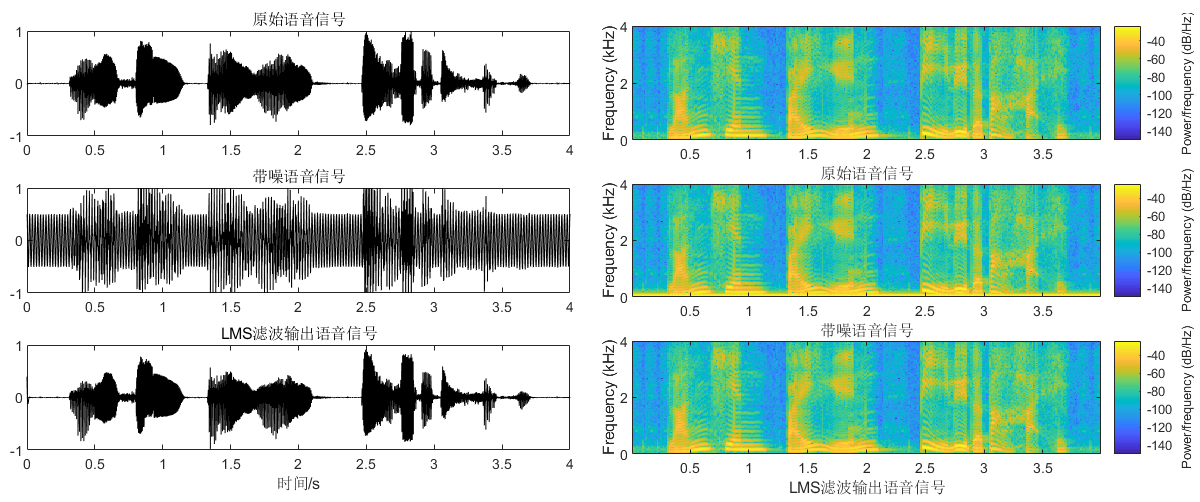
![波形图和语谱图]()
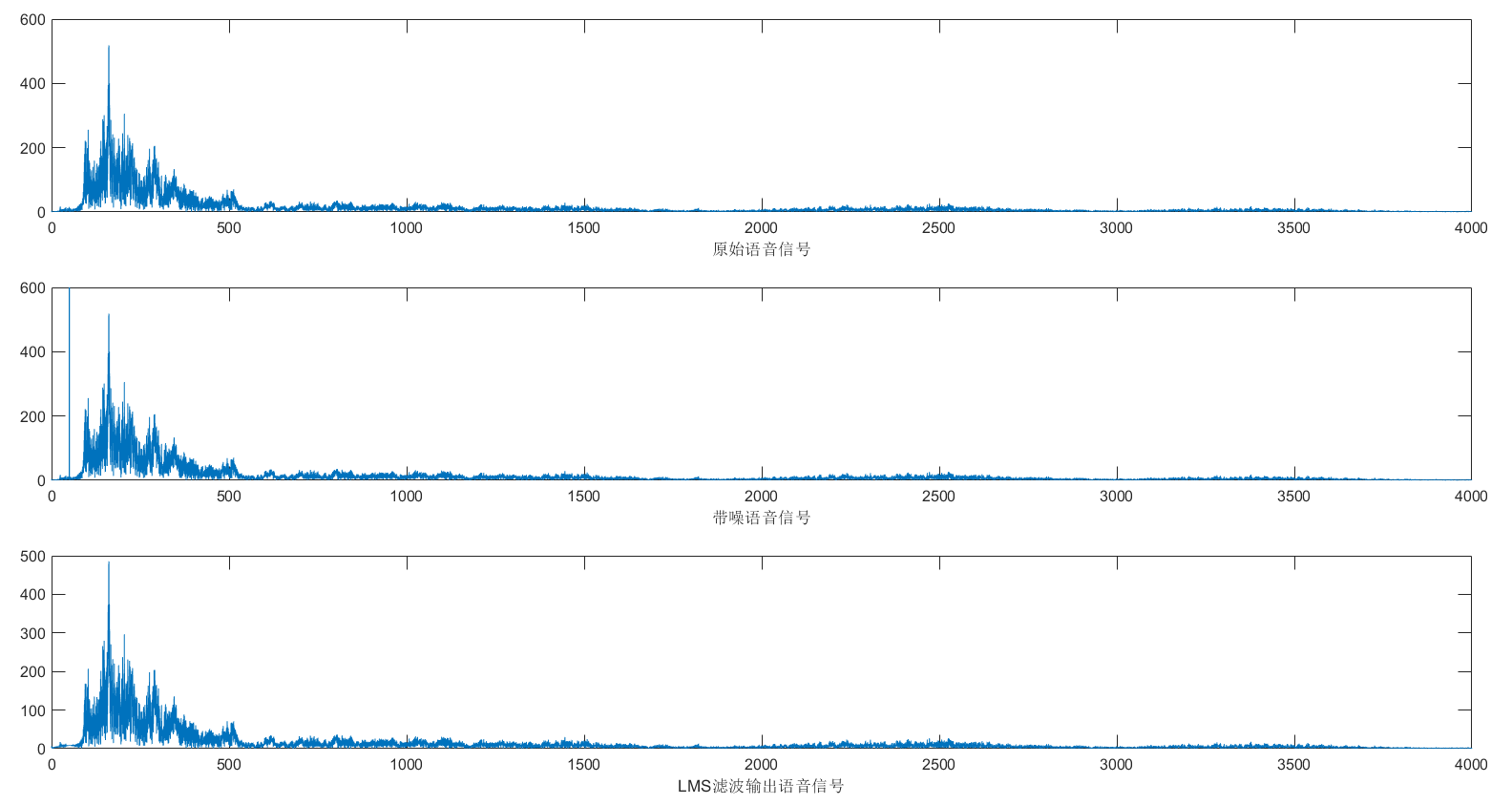
![频谱图]()
可以发现语谱图上单波噪声还是很干净的,在频谱图上可以发现50Hz的频率噪声被减掉了。
博客案例 – LMS
clc;
clear all;
close all;
Fs = 500;
t = 0:1/Fs:3;
t = t';
Size_t = size(t,1);
F1 = 7;
F2 = 13;
F3 = 23;
F4 = 50;
SNR = -100;
Signal = 10^(SNR/20)*(sin(2*pi*F1*t) + 0.5*sin(2*pi*F2*t) + 0.25*sin(2*pi*F3*t));
Signal = Signal/max(Signal) ;
noise = 0.95*sin(2*pi*F4*t+pi/2);
Signal_noise = Signal + noise;
M = 2;
Signal_Len = Size_t;
niu = 0.1;
y_out = zeros(Signal_Len,1);
error_out = zeros(Signal_Len,1);
w_out = zeros(Signal_Len,M);
for i=1:Signal_Len
if i == 1
w = zeros(M,1);
x = zeros(M,1);
end
d = Signal_noise(i);
x = [sin(2*pi*F4*(i-1)/Fs)
cos(2*pi*F4*(i-1)/Fs)];
y = x' * w;
error = d - y;
w_forward = w + niu * error * x;
w = w_forward;
y_out(i) = y;
error_out(i) = error;
w_out(i,:) = w';
end
subplot(2,1,1);
plot(t,Signal);
title('原始信号');
xlabel('时间t/s');
subplot(2,1,2);
plot(t,Signal_noise);
title('加入干扰噪声的信号');
xlabel('时间t/s');
figure;
subplot(2,1,1);
plot(t,y_out);
title('滤波器输出');
xlabel('时间t/s');
subplot(2,1,2);
plot(t,error_out,'b');
title('输出误差');
xlabel('时间t/s');
figure;
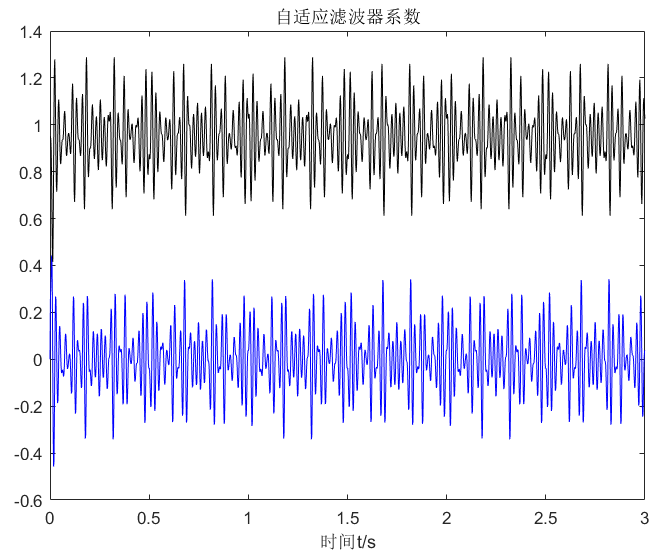
plot(t(1:Signal_Len),w_out(:,1),'r',t(1:Signal_Len),w_out(:,2),'b');
title('自适应滤波器系数');
xlabel('时间t/s');
|
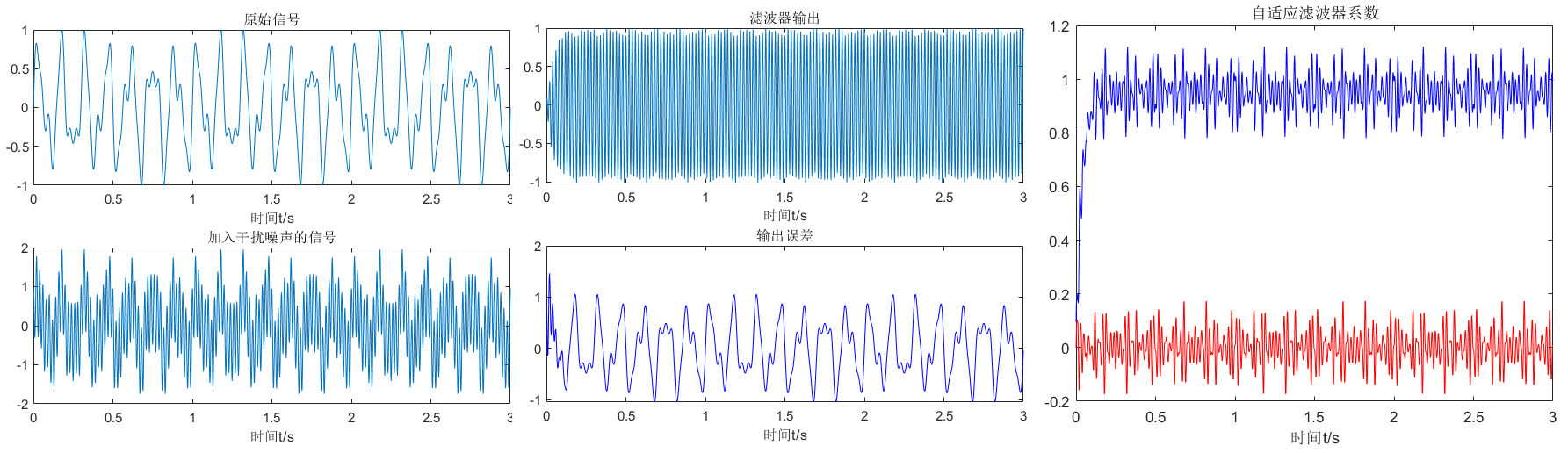
![]()
如果调整步长控制因子可以发现,滤波器系数需要更长的时间才会趋向稳定,最终的头部的降噪效果要打折扣。
4. RLS递归最小二乘
前言
若从代价函数的收敛方式来分,可以分为最小二乘法和梯度下降法。LMS为梯度下降法,但是通过上述实验可以发现,权重系数收敛是需要时间的,这点取决于步长。这导致了前几秒的滤波效果很差。递归最小二乘法(RLS)能有效的解决这个问题,收敛速度比LMS/NLMS收敛快一个数量级。
RLS的算法原理简述
详细理论推导可见文献👉【3】
RLS算法的关键在于用二乘方的时间平均准则取代最小均方准则,并按照时间进行迭代计算。如下:
LMS中为最小均方准则(集总平均):
J(k)=∥E[e(k)2]∥
RSL为时间平均(实数)
ϵ(n)=k=0∑ne2(k)=min
这里多考虑了一步,类似于移动加权平均,加入一个权重,让“新声音”的权重越大,即
minJn(w)=i=0∑nλn−i∣e(i)∣2=i=0∑nλn−i∣∣y(i)−wT(n)x(i)∣∣2
0<λ≤1为遗忘因子,这里只讨论平稳情况,取λ=1。
步骤一:初始化
w(0)=0,P(0)=δ−1I(0<δ≪1)
其中δ为很小的正数,如1e-7。
当SNR较高时,δ取小正数;当SNR较低时,δ取大正数。
步骤二:迭代更新
-
计算中间量π(n),可减轻有限精读计算带来的问题
π(n)=P(n−1)x(n)
-
计算增益向量k(n)
k(n)=λ+xT(n)π(n)π(n)
-
计算先验估计误差
ϵ(n)=y(n)−wT(n−1)x(n)
-
更新滤波器系数
w(n)=w(n−1)+k(n)ϵ∗(n)
-
更新逆相关矩阵
P(n)=λ1[P(n−1)−k(n)xH(n)P(n−1)]
函数部分
function [e,w]=rls(lambda,M,u,d,delta)
w=zeros(M,1);
P=eye(M)/delta;
u=u(:);
d=d(:);
N=length(u);
e=d.';
for n=M:N
uvec=u(n:-1:n-M+1);
e(n)=d(n)-w'*uvec;
k=lambda^(-1)*P*uvec/(1+lambda^(-1)*uvec'*P*uvec);
P=lambda^(-1)*P-lambda^(-1)*k*uvec'*P;
w=w+k*conj(e(n));
end
end
|
应用实例
博客案例 – RLS
clc;clear all; close all;
Fs = 500;
t = 0:1/Fs:3;
t = t';
Size_t = size(t,1);
F1 = 7;
F2 = 13;
F3 = 23;
F4 = 50;
SIR = -100;
Signal = 10^(SIR/20)*(sin(2*pi*F1*t) + 0.5*sin(2*pi*F2*t) + 0.25*sin(2*pi*F3*t));
Signal = Signal/max(Signal) ;
noise = 0.95*sin(2*pi*F4*t+pi/2);
Signal_noise = Signal + noise;
M = 2;
lamda = 0.90;
Signal_Len = Size_t;
I = eye(M);
c = 0.0001;
y_out = zeros(Signal_Len,1);
Eta_out = zeros(Signal_Len,1);
w_out = zeros(Signal_Len,M);
for i=1:Signal_Len
if i == 1
P_last = I/c;
w_last = zeros(M,1);
end
d = Signal_noise(i);
x = [sin(2*pi*F4*(i-1)/Fs)
cos(2*pi*F4*(i-1)/Fs)];
K = (P_last * x)/(lamda + x'* P_last * x);
y = x'* w_last;
Eta = d - y;
w = w_last + K * Eta;
P = (I - K * x')* P_last/lamda;
P_last = P;
w_last = w;
y_out(i) = y;
Eta_out(i) = Eta;
w_out(i,:) = w';
end
figure;
subplot(3,1,1);
plot(t,Signal);
title('原始信号');
xlabel('时间t/s');
subplot(3,1,2);
plot(t,Signal_noise);
string = ['加入50Hz工频干扰的信号,信干比SIR = ',num2str(SIR),'dB'];
title(string);
xlabel('时间t/s');
subplot(3,1,3);
plot(t,Eta_out,'b',t,Signal,'r');
legend('滤波后结果','原始信号')
title('输出误差');
xlabel('时间t/s');
set(gcf,'color','w')
figure(2);
plot(t, w_out(:,1),'b',t,w_out(:,2),'k')
set(gcf,'color','w')
title('自适应滤波器系数');
xlabel('时间t/s');
|
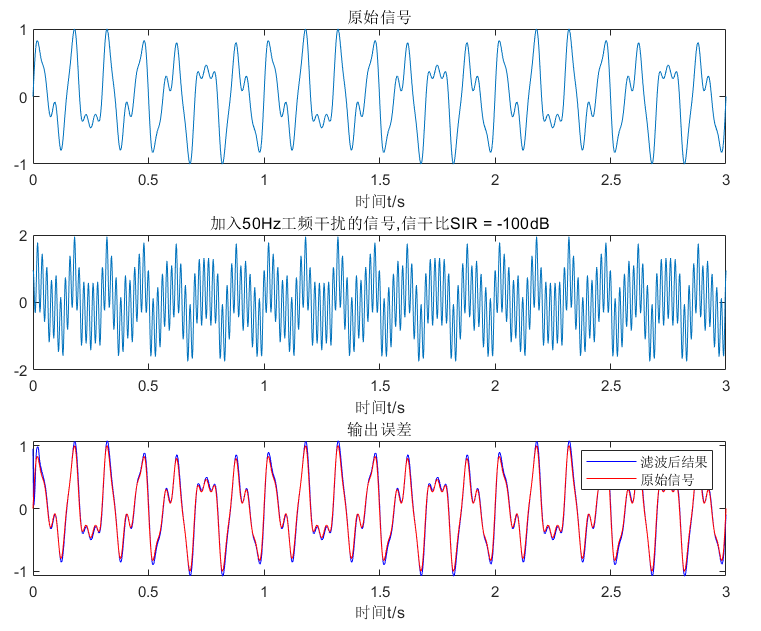
结果查看:
| 波形图对比 |
滤波器系数 |
![]() |
![]() |
通过结果可以发现,RSL基本没有收敛的过程,出道即收敛。毕竟是最小二乘法。
参考网址:
-
https://www.cnblogs.com/augustine0654/p/10041313.html
-
https://wenku.baidu.com/view/8fc14ec6b90d6c85ed3ac6c2.html
-
RSL详细推导–博客园【桂】
-
RSL算法说明–CSDN
-
简述LMS、RSL、最陡下降法理论
![]()