原理总结：

• 对偶的目的：使用核技巧

$L = \sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy^{(i)}y^{(j)}x^{(i)^T}x^{(j)}$

• 求极小值的方法：SMO算法

• 预测函数：

  $\hat{y}=w^Tx+b=\sum_{i=1}^m\alpha_iy^{(i)}x^{(i)T}x+b$

• 核技巧：

  $\hat{y}=\sum_{i=1}^m\alpha_iy^{(i)}K(x^{(i)},x)+b$

• 常用核函数：

  • 多项式核函数：

    $K(x^{(i)},x^{(j)})=(\gamma x^{(i)T}x^{j}+c)^n$

    当 n = 1 ，$\gamma = 1 $ c = 0 时，是线性核函数。

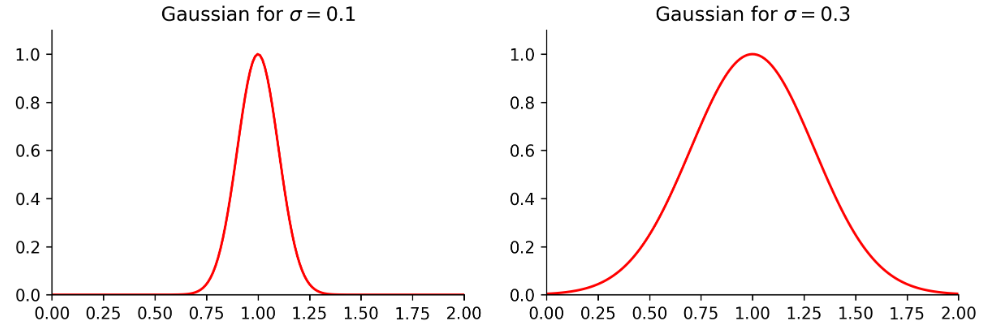
  • 高斯核函数：

    $K(x^{(i)},x^{(j)})=exp(-\frac{(x^{(i)}-x^{(j)}}{2\sigma ^2})=exp(-\gamma\cdot (x^{(i)}-x^{(j)})^2)$

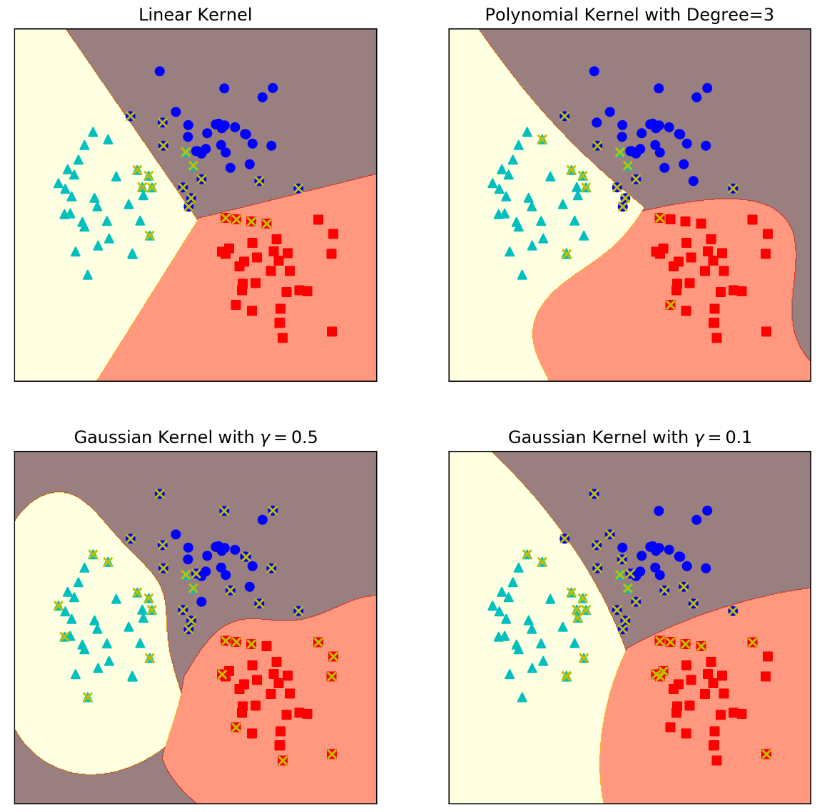
  核函数根据$\hat{y}$的公式可知，核函数是以支持向量为中心作用的。预测函数是中心点在支持向量处的高斯函数的线性组合。其线性组合的系数为$\alpha_iy^{(i)}$,也即反钟型函数的线性组合。

以上的图来源于：https://nbviewer.jupyter.org/github/wangjs-jacky/Jupyter-notebook/blob/master/03_黄永昌_skleran基础0/ch08.01.ipynb

Example01：不同参数下的SVM

Example02:乳腺癌案例

• 根据数据规模与特征的比重选择方法

  • 样本很少，特征很多【DNA；文本处理】：线性SVM或者Logistics回归
  • 样本少，特征中等：高斯核函数
  • 样本很多，特征少【房子特征】：会出现欠拟合，需要通过PolynomailFeatures增加特征多项式，推荐多项式核函数或者高斯核函数。

• 方法分析：

  • 线性核函数：
    • 简单，直观，运算效率高
    • 缺点：无法线性不可分
  • 多项式核函数：
    • 需要提前输入的超参数太多：$\gamma 、c 、degree$
    • 拟合的阶数不能太高，尤其当$x^{(i)T}x^{(j)}>1$时，映射后的值非常大，函数不够稳定。
  • 高斯核函数：
    • 映射到无限维向量空间，所以非线性很强，比起多项式核函数，其映射后的值始终在[0,1]之间。且参数就一个$\gamma$需要确定。
    • 缺点：计算速度慢，容易过拟合。