逻辑回归的核心公式

成本函数：

$J(\theta)=-\frac{1}{m}[\sum_{i=1}^my_ilog(h_\theta(x_i)+(1-y_i)log(1-h_{\theta}(x_i))]$

梯度下降算法：

$\theta_j = \theta_j -\alpha \frac{\partial}{\partial\theta_j}J(\theta)$

将求导后的成本函数代入：

$\theta_j = \theta_j -\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x_i)-y_i)x_i^{(j)}$

加入正则化：

成本函数：

$J(\theta)=-\frac{1}{m}[\sum_{i=1}^my_ilog(h_\theta(x_i)+(1-y_i)log(1-h_{\theta}(x_i))]+\lambda\sum_{j=1}^n\theta_j^2$

梯度下降【权重衰减】：

$\theta_j = \theta_j(1-\alpha\frac{\lambda}{m}) -\alpha\frac{1}{m}\sum_{i=1}^m(h_\theta(x_i)-y_i)x_i^{(j)}$

Example01：L1和L2范数的讲解

观察加入正则项后的成本函数：

$J(\theta) = Cost\ + \lambda \cdot 正则项$

若只考虑Cost函数，根据权重衰减可知，任意在下图中找一个点，开始迭代，会不断的靠近虚线的正法线方向移动。

若只考虑正则项部分，则越靠近原点，则正则项部分越小。

故两者都希望往各自的最低点处移动。

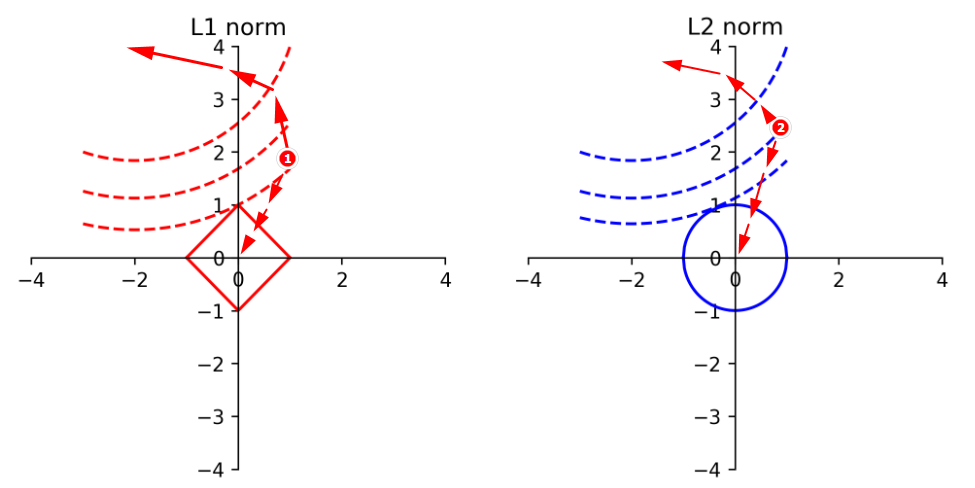
数无型时少直觉：可以想象虚线部分代表的是一个不规则的分布，而L1范数在空间中是一个锥形分布。所以以上两张图在三维中是两个分布的叠加，现在就是在找这个新分布的最小值，在原两个分布的交点处取到。

特点：
- L1：可以让大部分的特征都取到0，可以作为降维的一个操作
- L2：保留原有的所有特征，但是赋予每个特征一个权重。

Example02：乳腺癌实例

需要注意的是：重复特征有的时候是需要的

速度：可由路径/ 时间得到。不代表速度这个复合特征是多余的，这个反映了事物内在逻辑关系的体现。

提取特征时，不妨从事务的内在逻辑关系入手，分析已有特征之间的关系
乳腺癌中，完全独立的特征有10个特征，通过数值手段（标准差，最大值等）构造的特征一共有30个特征。
cancer.feature_names

分析真实标签和预测标签

y_pred = model.predict(X_test)
np.equal(y_pred,y_test).shape[0]

这里还说明了score 与准确率之间的关系，即使全部预测出来了，score也并非是满分。
- 准确性的计算依据的是：model.predict
- 而score的计算依据的是： model.predict_proba

这里通过L1范数来降维，值得注意的是定义Pipeline的写法，对于其中的字典函数接受的时候，不指定Key的具体值，需要在定义函数的时候加上**kwarg

def polynomial_model(degree=1, **kwarg):
    polynomial_features = PolynomialFeatures(degree=degree,
                                             include_bias=False)
    logistic_regression = LogisticRegression(**kwarg)
    pipeline = Pipeline([("polynomial_features", polynomial_features),
                         ("logistic_regression", logistic_regression)])
    return pipeline