极零图

转移函数的分子、分母多项式可以分别做因式分解，得：

$H(z) = g z^{N-M}\frac{\prod_{r=1}^M(z-z_r)}{\prod_{r=1}^N(z-p_k)}$

式中g为系统的增益因子

将上式$H(z)$的极点和零点画在z平面上得到的图形可称为极零图

根据极零图分析频率响应

若要通过极零图判断系统的频率响应，则必须在z平面上的单位圆上取值，即令$z = e^{jw}$

$H(e^{jw}) = g e^{j(N-M)w}\frac{\prod_{r=1}^M(e^{jw}-z_r)}{\prod_{r=1}^N(e^{jw}-p_k)}$

系统幅频响应：

$|H(e^{jw})| = g \frac{\prod_{r=1}^M|e^{jw}-z_r|}{\prod_{r=1}^N|e^{jw}-p_k|}$

系统相频响应：

$\varphi\left(\mathrm{e}^{\mathrm{W}}\right)=\arg \left[\mathrm{e}^{(N-M) \alpha}\right]+\sum_{r=1}^{M}\left[\arg \left(\mathrm{e}^{\mathrm{i} \omega}-z_{r}\right)\right]-\sum_{k=1}^{N}\left[\arg \left(\mathrm{e}^{\mathrm{W}}-p_{k}\right)\right]$

极零分析实例

例题 ：一个LSI系统的差分方程是

$y(n) = x(n) - 4x(n-1) + 4x(n-2)$

试用极零分析画出该系统的幅频响应及相频相应。

将差分方程进行$Z$变换，得到系统的转移函数：

$H(z) = 1 - 4z^{-1} + 4z^{-2} =\frac{z^2-4z+4}{z^2} = \frac{(z-2)^2}{z^2}$

首先该系统是$FIR$系统，零点在$z=2$处有二阶重零点，在$z=0$有二阶重极点。

系统的幅频响应：

$|H(e^{jw})| = \frac{|e^{jw}-2|^2}{|e^{jw}-0|^2}=\frac{|e^{jw}-2|^2}{1}=\frac{r_1^2}{r_2^2}$

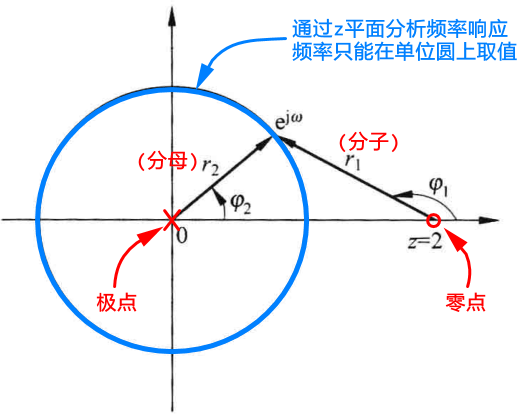
幅频响应分析：

• 当$w=0$时，$r_1=r_2=1$，$|H(e^{j0})|=1$

• 当$w$由0增加到$\pi$时，$r_1>r_2$，$|H(e^{j0})|$递增

• 当$w=\pi$时，$r_1=3,r_2=1$，所以$|H(e^{jw})=9|$达到最大值

• 由$w$由$\pi$变到$2\pi$时，$|H(e^{jw})|$又由9减少到1。

极零点分配实例 -- 滤波

分配原则：

• 零点代表分子；极点代表分母。

• 若将零点分配在圆环上，则使设计的滤波器拒绝对应的那个频率。

• 极点不能分配到圆环上，若极点离圆环越近，$|H(z)|$在频域的放大作用越大，即允许该频率通过

具体分配实例课件例题 2.5.4：

• 低通滤波器：零点放在高频，极点放在低频

• 高通滤波器：零点放在低频，极点也放在低频（也可放高频）

• 带通滤波器：零点在低频和高频各放一个

  注：若零点两个，则极点必须也要两个，需要共轭放置

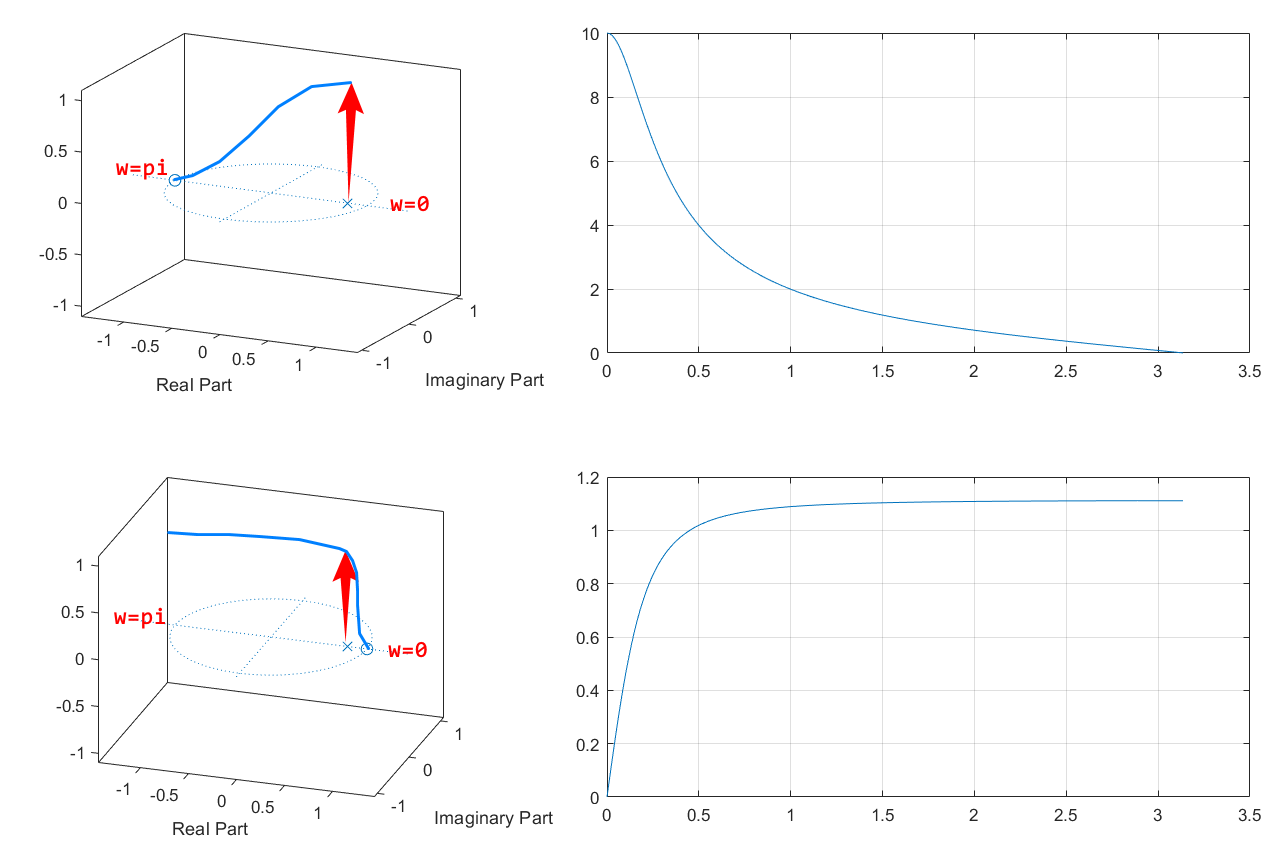
例题 2.5.4

$\begin{array}{l} H_{0}(z)=a \frac{1+z^{-1}}{1-p z^{-1}} \\ H_{1}(z)=b \frac{1-z^{-1}}{1-p z^{-1}} \\ H_{2}(z)=c \frac{\left(1+z^{-1}\right)\left(1-z^{-1}\right)}{\left(1-r \mathrm{e}^{\mathrm{i} \alpha} z^{-1}\right)\left(1-\mathrm{re}^{-\mathrm{i} \omega} z^{-1}\right)} \end{array}$

其幅频响应，极零点分布状况，单位冲击响应为：

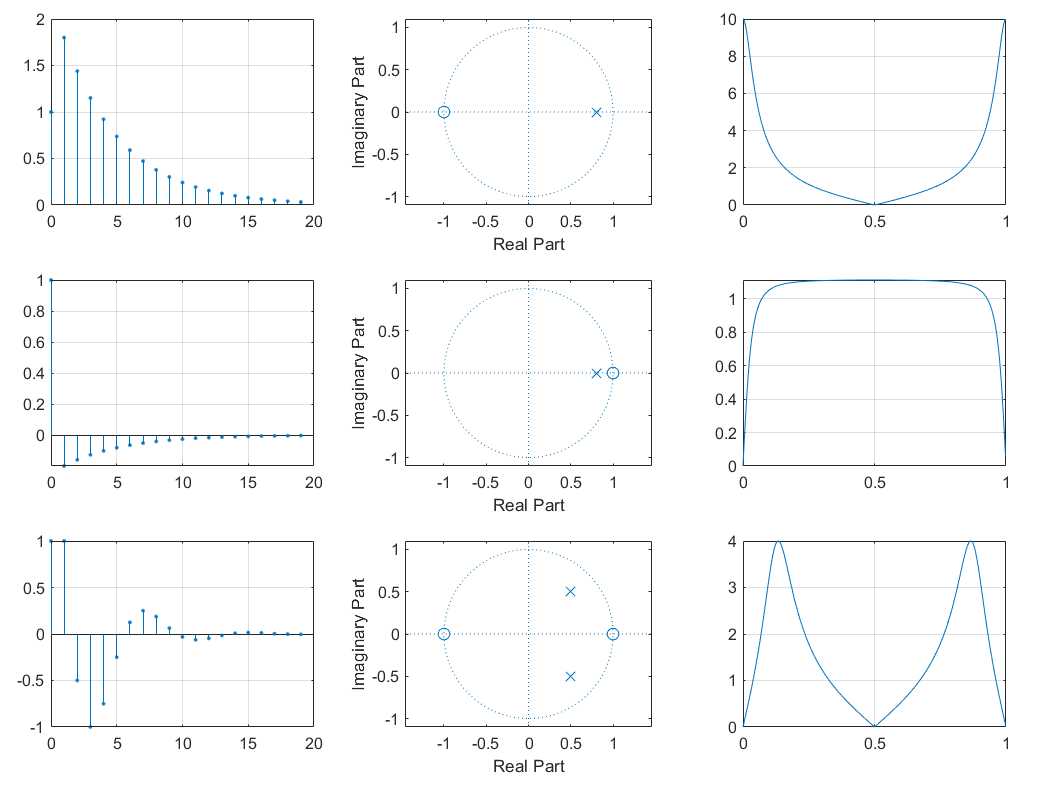
其中，系数$a,b,c$是用来使幅值调整为1。

Matlab代码：

%%
b_1 = [1,1];a_1 = [1,-0.8];
b_2 = [1,-1];a_2 = [1,-0.8];
% zp2tf可以根据极零点，算出系数a和b
z = [-1,1]';p = [0.5+0.5i,0.5-0.5i]';
[b_3,a_3] = zp2tf(z,p,1);

[h_1,t_1] = impz(b_1,a_1,20);
[H_1,w_1] = freqz(b_1,a_1,512,'whole',1);Hr_1 = abs(H_1);
[h_2,t_2] = impz(b_2,a_2,20);
[H_2,w_2] = freqz(b_2,a_2,512,'whole',1);Hr_2 = abs(H_2);

subplot 331;stem(t_1,h_1,'.');grid on;
subplot 332;zplane(b_1,a_1);
subplot 333;plot(w_1,Hr_1);grid on;
subplot 334;stem(t_2,h_2,'.');grid on;
subplot 335;zplane(b_2,a_2);
subplot 336;plot(w_2,Hr_2);grid on;

[h_3,t_3] = impz(b_3,a_3,20);
[H_3,w_3] = freqz(b_3,a_3,512,'whole',1);Hr_3 = abs(H_3);

subplot 337;stem(t_3,h_3,'.');grid on;
subplot 338;zplane(b_3,a_3);
subplot 339;plot(w_3,Hr_3);grid on;
set(gcf,'color','w')

Matlab代码示例

系统可以通过转移函数来定义：

$H(z) = \frac{B(z)}{A(z)} = \frac{b(1)+b(2)z^{-1}+b(3)z^{-2}+\dots+b(n_b+1)z^{-n_b}}{1+a(2)z^{-1}+a(3)z^{-2}+\cdots+a(n_a+1)z^{-n_a}}$

分子和分母的系数为：

$b = [b(1),b(2),\dots,b(n_b+1)]\\ a = [a(1),a(2),\dots,a(n_b+1)]$

1. filter.m

本文件可以根据转移函数系数求一个离散系统的**时域输出。**即，

$y(n) = x(n) * h(n)$

上式中，$h(n)$可以通过系数$a$和$b$表出，

$\begin{aligned} y(n)=& b(1) x(n)+b(2) x(n-1)+\cdots+b\left(n_{b}+1\right) x\left(n-n_{b}\right) \\ &-a(2) y(n-1)-\cdots-a\left(n_{a}+1\right) y\left(n-n_{a}\right) \end{aligned}$

调用格式：y=filter(b,a,x)

---

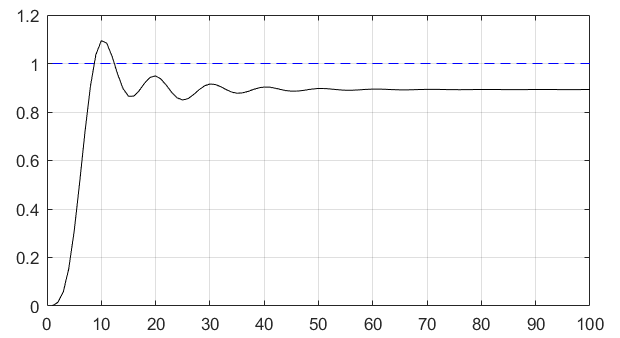
**例题：**求系统的阶跃相应（所谓阶跃响应是系统对阶跃输入的输出）

$H(z)=\frac{0.001836+0.007344 z^{-1}+0.011016 z^{-2}+0.007374 z^{-3}+0.001836 z^{-4}}{1-3.0544 z^{-1}+3.8291 z^{-2}-2.2925 z^{-3}+0.55075 z^{-4}}$

Matlab代码：

x = ones(100);t = 1:100;
b = [.001836,.007344,.011016,.0073774,.001836];
a = [1,-3.0544,3.8291,-2.2925,.55075];
y = filter(b,a,x);
plot(t,x,'b--',t,y,'k-');grid on;
set(gcf,'color','w');

2.impz.m

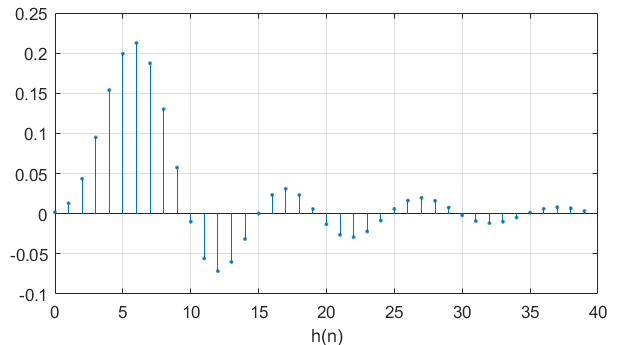
本文件可以用来求出系统的单位抽样响应$h(n)$，调用格式是

调用格式：[h,t]=impz(b,a,N)

Matlab编程：

[h,t] = impz(b,a,40);stem(t,h,'.');grid on;
set(gcf,'color','w');

3. freqz.m

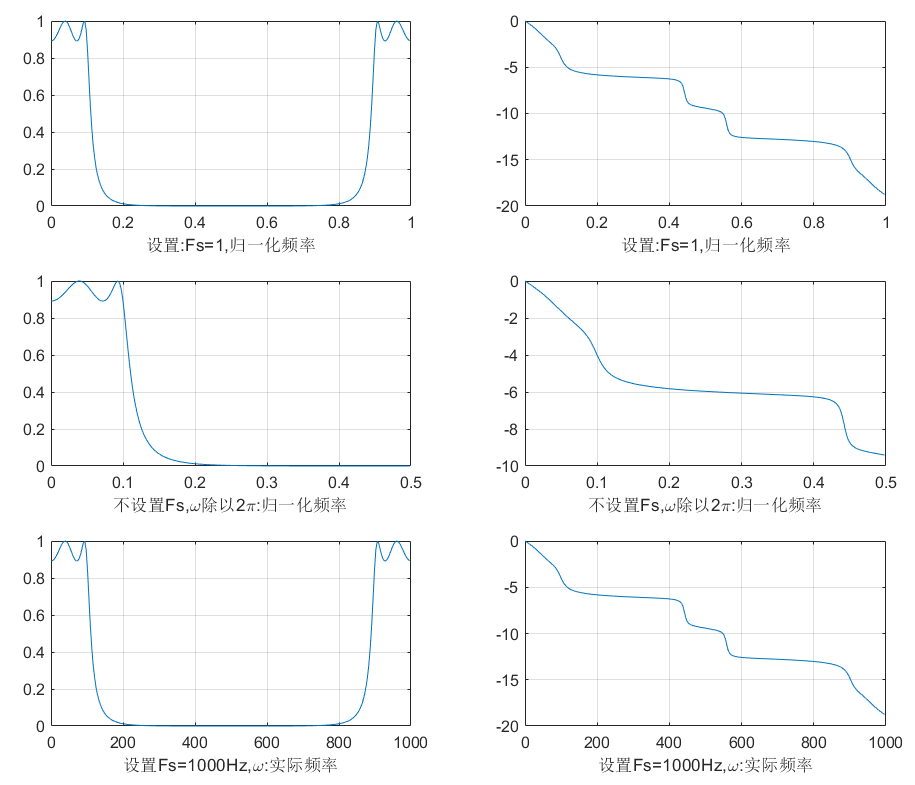
根据系数a和b，求出系统的幅频响应$H(e^{jw})$

调用格式：[H,w]=freqz(b,a,N,'whole',Fs)

其中，N是频率轴的分点数，建议为2的幂；w是返回频率轴坐标向量；若Fs=1，频率轴给出归一化频率；whole指定计算的频率范围是$0 \sim Fs$，默认是$0 \sim Fs/2$

三种调用格式：

Matlab代码：

% 格式1
[H,w] = freqz(b,a,256,'whole',1);
Hr = abs(H);
Hphase = angle(H);Hphase = unwrap(Hphase);
subplot 321;plot(w,Hr);grid on;xlabel('设置:Fs=1,归一化频率')
subplot 322;plot(w,Hphase);grid on;
xlabel('设置:Fs=1,归一化频率')
% 格式2
[H,w] = freqz(b,a,256);
Hr = abs(H);
Hphase = angle(H);Hphase = unwrap(Hphase);
subplot 323;plot(w/(2*pi),Hr);grid on;xlabel('不设置Fs,\omega除以2\pi:归一化频率');xlim([0,0.5]);
subplot 324;plot(w/(2*pi),Hphase);grid on;xlabel('不设置Fs,\omega除以2\pi:归一化频率');xlim([0,0.5]);
set(gcf,'color','w');
% 格式3
[H,w] = freqz(b,a,256,'whole',1000);
Hr = abs(H);
Hphase = angle(H);Hphase = unwrap(Hphase);
subplot 325;plot(w,Hr);grid on;xlabel('设置Fs=1000Hz,\omega:实际频率')
subplot 326;plot(w,Hphase);grid on;xlabel('设置Fs=1000Hz,\omega:实际频率')

set(gcf,'color','w');

#

4. zplane.m

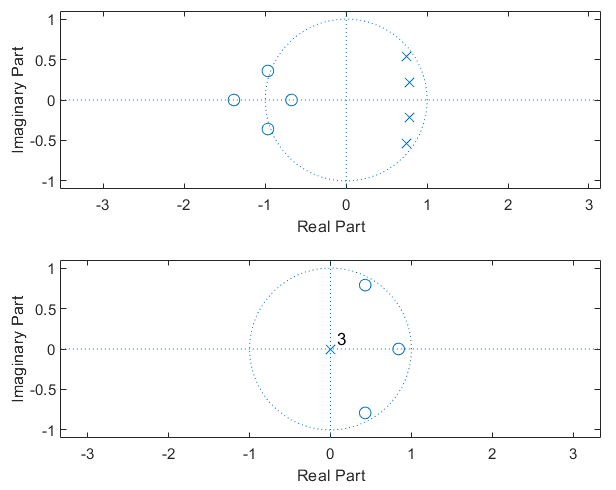
调用格式：zplane(z,p) 以及 zplane(b,a)

例如：求FIR系统的极零图

$H(z) = 1 -1.7z^{-1}+1.53z^{-2} - 0.648z^{-3}$

Matlab编程：

b = [.001836,.007344,.011016,.007374,.001836];
a = [1,-3.0544,3.8291,-2.2925,.55075];
subplot 211;zplane(b,a);
b = [1,-1.7,1.53,-0.68];
a = 1;
subplot 212;zplane(b,a);
set(gcf,'color','w')

5. zp2tf.m

已知零极点$z$和$p$，可以转化为系数$a$和$b$：

Matlab编程：

z = [-1,1]';p = [0.5+0.5i,0.5-0.5i]';
[b_3,a_3] = zp2tf(z,p,1);
[h_3,t_3] = impz(b_3,a_3,20);
[H_3,w_3] = freqz(b_3,a_3,512,'whole',1);Hr_3 = abs(H_3);
subplot 331;stem(t_3,h_3,'.');grid on;xlabel('h(n)')
subplot 332;zplane(b_3,a_3);
subplot 333;plot(w_3,Hr_3);grid on;xlabel('幅频图')
set(gcf,'color','w')