在信号处理中经常要研究两个信号的相似性，以及一个信号经过一段延迟后自身的相似性。

为什么要用相关函数表示相似度？

之前研究两个信号的相似性，我们会用归一化相关系数来表征：

$\rho_{xy}=\frac{\sum_{n=0}^\infin x(n)y(n)}{[\sum_{n=0}^\infin x^2(n)\sum_{n=0}^\infin y^2(n)]^{1/2}}$

其中定义相关系数：

$r_{xy} = \sum_{n=0}^\infin x(n)y(n)$

• 当$x(n)=y(n)$时，$\rho_{xy}=1$，两个信号完全相关，这是$r_{xy}$取最大

• 当$x(n)$ 与$y(n)$完全无关时，$r_{xy}=0,\rho_{xy}=0$

• 当$x(n)$ 与$y(n)$存在某种程度的相似时，$r_{xy}\ne 0,|\rho_{xy}|$在 0 和 1 中间取值

但是相关函数存在局限性，如正余弦信号。正弦和余弦具有很大的相似性，但是计算$\rho_{xy}=r_{xy}=0$

相关函数的定义

x(n)​为能量信号

自相关函数：

$r_x(m) = \sum_{n=-\infin}^{\infin}x(n)x(n+m)$

互相关函数:

$r_{xy}(m) = \sum_{n=-\infin}^{\infin}x(n)y(n+m)$

注：互相关函数不满足交换性，满足：

$r_{xy}(m) = r_{yx}(-m)$

不满足的原因是，后面那个信号是延迟，所以互相关函数的还有的定义也可为：

$r_{xy}(m)=\sum_{n=-\infin}^{\infin}x(n-m)y(n)$

x(n)​为功率信号

研究$r_x(0)$可以发现：

$r_x(0)=\sum_{n=-\infin}^{\infin}x(n)^2$

即$r_x(0)$等同于信号自身的能量，若信号不是能量信号，趋于无限大（功率信号），其相关函数定义为：

$r_{xy}(m) = \lim_{N\rightarrow\infin}\frac{1}{2N+1}\sum_{n=-N}^{N}x(n)y(n+m)$

进一步，若$x(n)$为周期信号，无限多个周期信号的求和，可用一个周期的求和平均代替

$r_x(m)=\frac{1}{N}\sum_{n=0}^{N-1}x(n)x(n+m)$

注：以上只是理论公式，实际中信号是有限长度的，实际代码公式见下

---

例题：令$x(n)=sin(wn)$，其周期为 N，即$w=\frac{2\pi}{N}$,求$x(n)$的自相关函数。

周期功率信号：

$\begin{aligned} r_x(m) =& \frac{1}{N}\sum_{n=0}^{N-1}x(n)x(n+m) =\frac{1}{N}\sum_{n=0}^{N-1}sin(wn)sin(wn+wm) \\ = & \cos (\omega m) \frac{1}{N} \sum_{n=0}^{N-1} \sin ^{2}(\omega n)+\sin (\omega m) \frac{1}{N} \sum_{n=0}^{N-1} \sin (\omega n) \cos (\omega n) \\ = & \frac{1}{2}cos(wm) \end{aligned}$

---

相关函数的应用

相关函数的应用很广，噪声中的信号检测，信号中隐含周期性的检测，信号相关性的检测，信号时延长度的测量等。相关函数还是描述随机信号的重要统计量。

观察的信号$x(n)$由真正的信号$s(n)$和白噪声$u(n)$所组成，即$x(n)=s(n)+u(n)$。假定$s(n)$是周期的，周期为$M$，$x(n)$的长度为$N$，那么$x(n)$的自相关

$\begin{aligned} r_x(m) = & \frac{1}{N} \sum_{n=0}^{N-1}[s(n)+u(n)][s(n+m)+u(n+m)] \\ =& r_s(m) + r_{us}(m)+r_{su}(m) + r_u(m) \end{aligned}$

式中：

• $r_{us}(m)$和$r_{su}(m)$是$s(n)$和$u(n)$的互相关，一般噪声是随机的，所以这两项会非常小。
• $r_u(m)$是噪声的自相关，就$m=0$时有值。
• 若$r_s(m)$是周期函数，则$r_x(m)$则也是呈现周期变换的，分别在周期点上呈现峰值。

---

例题：设信号$x(n)$由正弦信号加均值为零的白噪声组成，正弦信号幅值为 1，白噪声的方差为 1，时域波形图无法发现有正弦信号，但是根据**相关函数的性质（若原信号中周期，则相关函数也是周期信号）**可以分辨出正弦信号。

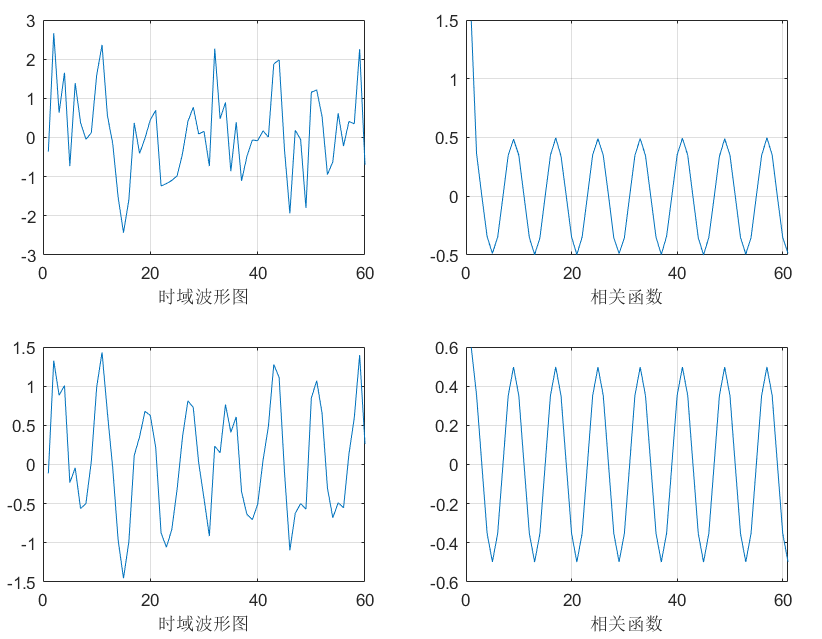
N = 50000;
p1 = 1;p2 = 0.1; % 设置功率
f = 1/8;
Mlag =60; % 选择m的长度，注要远远小于N
u = randn(1,N);
n = 0:N-1;
s = sin(2*pi*f*n);
x1 = u*sqrt(p1) + s ;rx1 = xcorr(x1,Mlag,'biased');
x2 = u*sqrt(p2) + s ;rx2 = xcorr(x2,Mlag,'biased');
% 绘图
subplot 221;plot(1:Mlag,x1(1:Mlag));grid on;xlabel('时域波形图')
subplot 222;plot(rx1(Mlag+1:end));grid on;xlabel('相关函数')
subplot 223;plot(1:Mlag,x2(1:Mlag));grid on;xlabel('时域波形图')
subplot 224;plot(rx2(Mlag+1:end));grid on;xlabel('相关函数')
set(gcf,'color','w')

Maltab 函数

均匀分布函数rand

通过直方图可以发现rand产生的是均匀分布的数据，时域图中看不出。

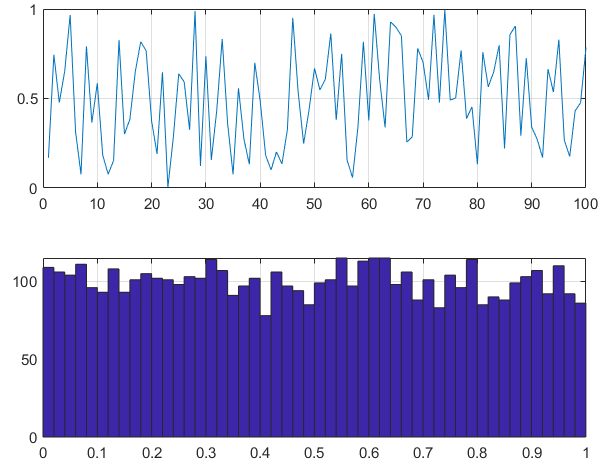
代码：

clear ;
N = 5000;u = rand(1,N);
u_mean = mean(u); % 0.5094
power_u = var(u); % 0.0812
subplot 211; plot(u(1:100));grid on ;
subplot 212; hist(u,50);grid on ;

var的数学公式：

$V = \frac{1}{N-1}\sum_{i=1}^N |A_i-\mu|^2$

---

产生一均匀分布、均值为零、功率为 0.01的白噪声信号$u(n)$。

其中$P=0.01$是希望达到的功率，通过调整信号的幅值可达到：

$\begin{aligned} P = & \frac{(u(n)/{a})^2}{N}\\ a =&\sqrt(u^2(n)/(N*P)) = \sqrt(\sigma^2_u/P) \end{aligned}$

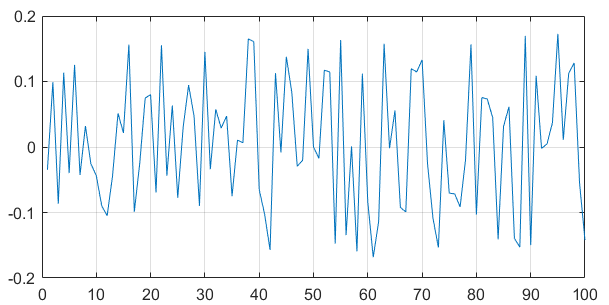
P = 0.01;
N = 5000;
u = rand(1,N);
u = u - mean(u);
a = sqrt(var(u)/P);u1 = u/a;
power_u1 = u1*u1'/N; % 0.0100
plot(u1(1:100));grid on;

高斯分布函数randn

产生零均值、功率为 0.1，服从高斯分布的白噪声信号$u(n)$

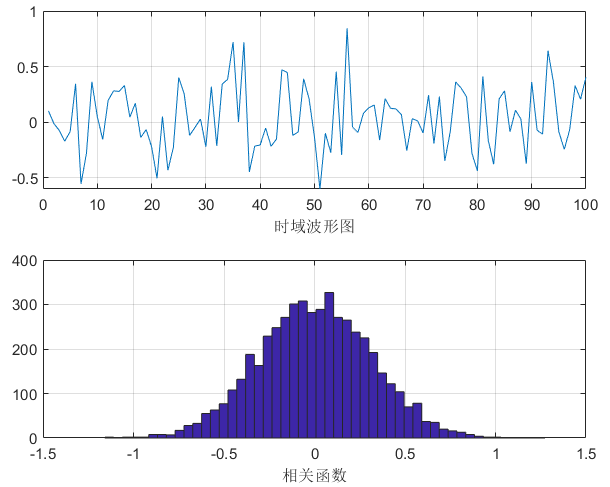
P = 0.1;
N = 5000;
u = randn(1,N);
a = sqrt(P);
u = u*a;
power_u = var(u);
subplot 211
plot(u(1:100));grid on;xlabel('时域波形图')
subplot 212
hist(u,50);grid on;xlabel('相关函数')
set(gcf,'color','w')

线性卷积conv

令$x(n)=(1,2,3,4,5),h(n)=(6,2,3,6,4,2),y(n)=x(n)*h(n)$，求$y(n)$

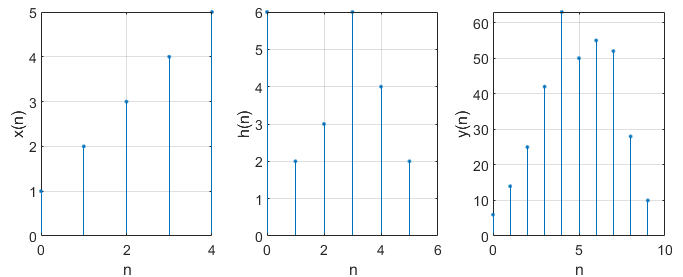
x=[1,2,3,4,5]; h=[6,2,3,6,4,2];
y=conv(x,h);
% 绘图
N=5;M=6;L=N+M-1;% 对应的长度为
nx=0:N-1; nh=0:M-1; ny=0:L-1; %横坐标
subplot 131; stem(nx,x,'.'); xlabel('n'); ylabel('x(n)'); grid on;
subplot 132; stem(nh,h,'.'); xlabel('n'); ylabel('h(n)');grid on;
subplot 133; stem(ny,y,'.'); xlabel('n'); ylabel('y(n)'); grid on;
set(gcf,'color','w')

注意观察卷积后的长度为：$L = N+M-1$

相关函数xcorr

在实际运算中，信号$x(n)$总是有限长，对应不同的$m$值，对应相乘与求和的数据长度是不同的，即

$r_x(m) = \frac{1}{N}\sum_{n=0}^{N-1-m}x_N(n)x_N(n+m)$

若 m 越大，使用信号的有效长度就越短，计算出的$r_x(m)$的性能就越差，要求$m<<N$。理论公式中能量信号与功率信号的相关函数公式不同，代码中一般都除以数据的长度 N。

自相关：rx=xcorr(x,m,'flag')

参数：

• flag=biased有偏估计，分母是$N$
• flag=unbiased无偏估计，分母是$N-m$

具体案例见相关函数的应用

这里调用程序存在两个问题？

1. 为什么这里 flag 要用有偏估计？

2. m 为什么要远远小于 N？

3. xcorr 不能用，需要平移一段

   >> x = [1,2,3]
   x =
        1     2     3
   >> xcorr(x)
   ans =
       3.0000    8.0000   14.0000    8.0000    3.0000