谱减法
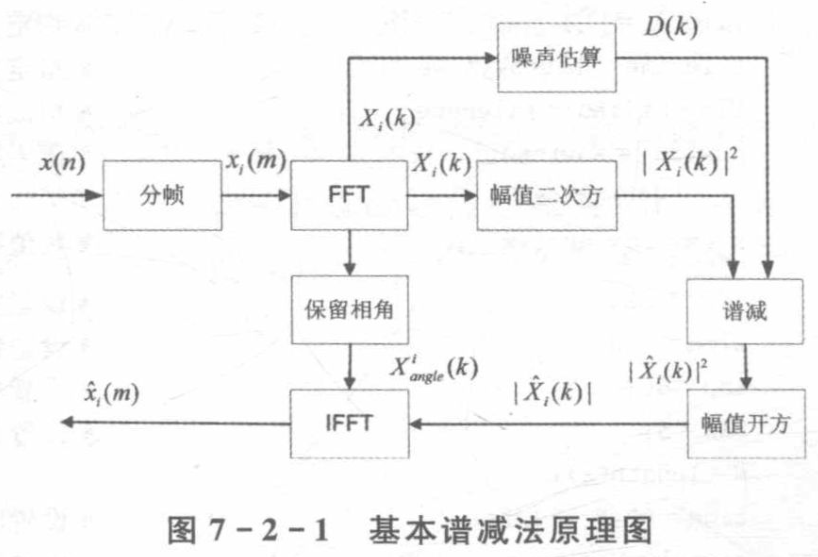
谱减算法为最早的语音降噪算法之一,基本原理:假设语音中的噪声只有加性噪声,只要将带噪语音谱减去噪声谱,就可以得到纯净语音幅度。这么做的前提是噪声信号是平稳的或者缓慢变化的。
噪声频谱
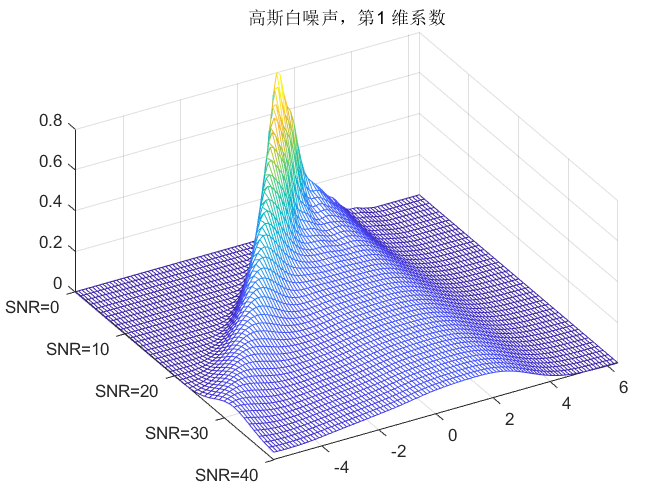
不同的噪音类型,有不同的稳定区间,以下根据肉眼选择,其中white完全无规律,无论是频域还是时域都是覆盖整张图。说明:频域图中上面一张图是随机选择一帧的频域图,下面是整段语音的平均频域图。
| type | wlen | time | 时域图 | 频域图 |
|---|---|---|---|---|
car |
200 | 12.5ms | 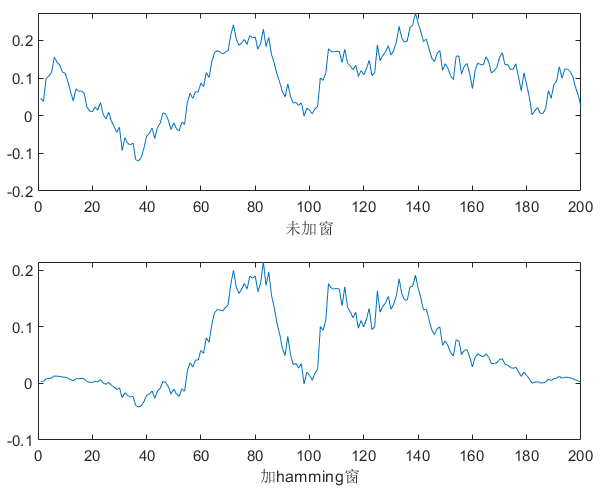 |
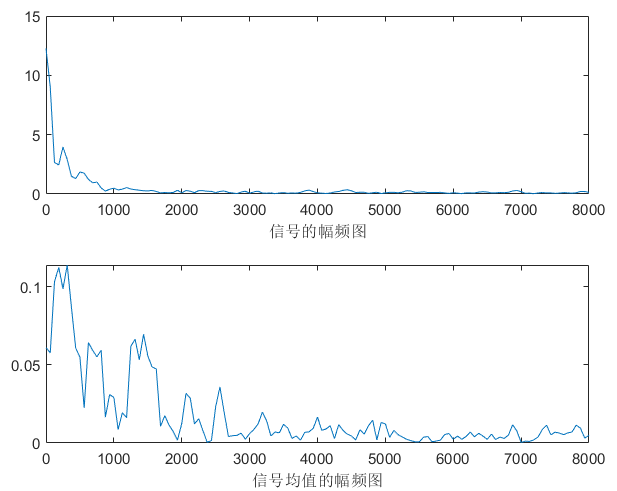 |
white |
400 | 25ms | 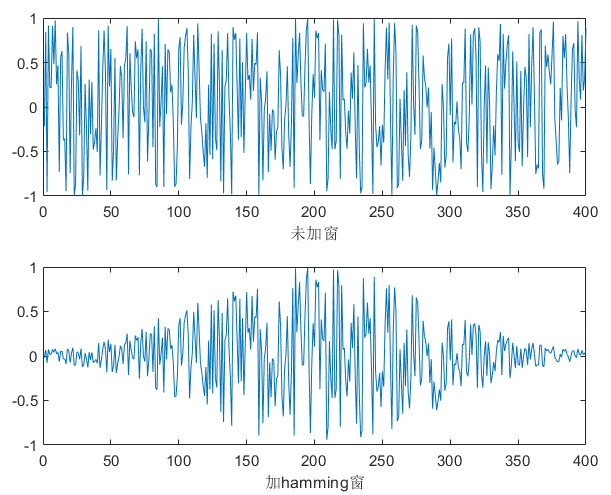 |
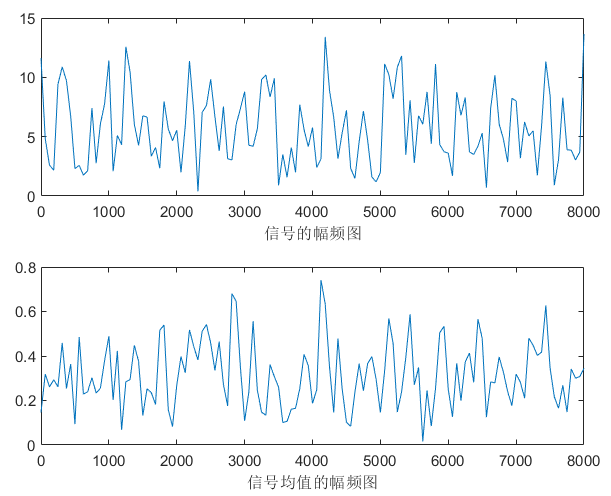 |
cafe |
1024 | 64ms | 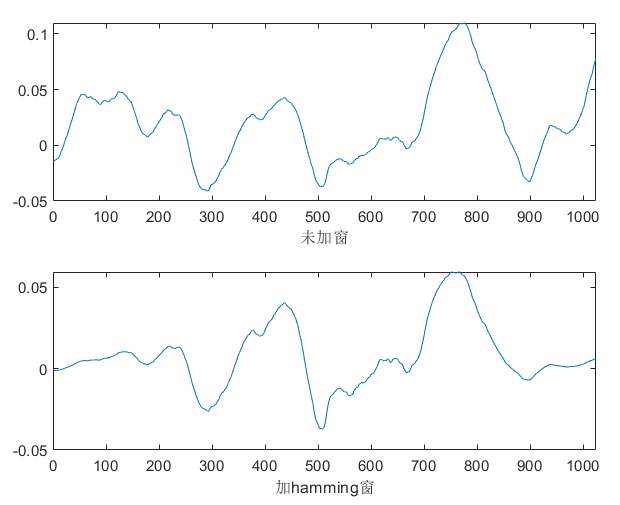 |
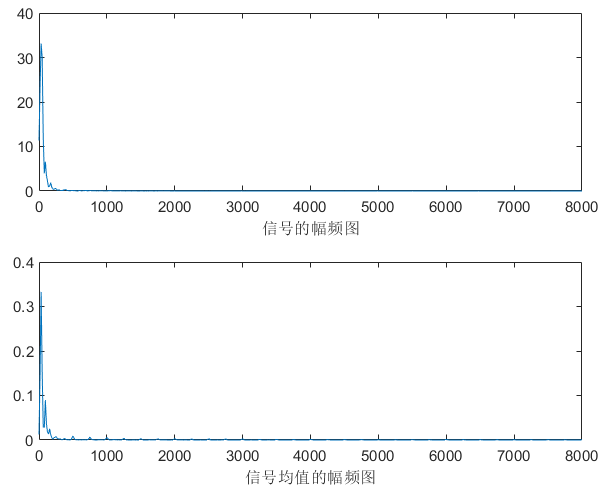 |
一般认为缓慢变化的含义是指包含1~3个周期波
例如当 Fs=8000 Hz,短时长=25ms,窗口长度可计算如下:
窗口长度 = 8000*0.025=200
原理
顾名思义,谱减法,就是用带噪信号的功率谱去噪声信号的功率谱。若时域信号相加,则频域谱也符合相加规律,那功率谱是否满足这种相加规律?
假设是纯净语音信号和加性噪声组成。其傅里叶后变换表示为:
如果功率谱表示可以写为:
若d(n)具有0均值,并且与x(n)不相关,则交叉项为0,则公式则可简化为:
具体流程
-
分帧
-
对每一帧做一次DFT
-
保留每个分量的幅值和相角,幅值是,相角为是
-
计算噪声段的平均能量值
-
谱减
其中为过减因子;称为增益补偿因子。
过减因子a:**范围大于等于1,主要影响语音谱的失真程度。在高信噪比中,a应取小值;对低信噪比中,a建议取大值。
**增益补偿因子b:**范围在0至1之间。可以控制残留噪声的多少以及音乐噪声的大小。
Berouti等人做了大量实验来确定alpha与beta的最优值,在这里我们直接使用就可以了。具体请参考论文:《Enhancement of speech corrupted by a acoustic noise》。
-
还原回时域,加上之存储的相角信息
![]()
音乐噪声和过减因子、谱下限的关系
若直接将带噪语音的幅度谱(或功率谱)直接与估计出来的噪声谱相减,有可能出现负值,早期的话直接设置下限为0,会导致信号频域谱的随机位置上出现小的,独立的峰值。
转换到时域后,会听到帧与帧之间的随机频率的多频音。(可能上一帧高频,下一帧低频)尤其在清音段尤其明显,这种由于半波整流?引起的“噪声”被称为**“音乐噪声”,可能导致音乐噪声**的原因为:
- 对谱减算法的负数部分进行了非线性处理(如:直接置零)
- 对噪声谱的估计不准
- 抑制函数具有较大的可变性
噪声估计流程
-
计算前导无语段语音NIS
-
根据NIS,利用对数谱距离的端点检测方法,调用
VAD -
根据每一帧的
SIGNALFLAG,对噪声进行平滑处理其中,Noise_old 是本帧以前的噪声平均幅值;Noise是本帧的复制普;L取9;Noise_new是通过带噪语音的噪声段计算出新的噪声平均幅值。
改进频谱
宋知用书本上介绍的方法
Boll改进
S.F.Boll 在1979年给出了一种改进的谱减法。由E.Zavarehel编写Matlab。
- Gamma 参数:
-
相邻帧的平滑处理
目的是为了得到较小的谱估计方差,下面的程序中,M=1
-
保留噪声的最大值
NRMNRM = max(NRM,YS(:,i)-N) % 把每帧的最大残差谱线保留到NRM中
比较每一条谱线残差判断是否小于
NRM,若小于,对第i帧第j条谱线将在相邻3帧之间找最小值的一条谱线。
SSBoll79.m
function output=SSBoll79(signal,fs,IS) |
CSDN中查到的改进方法
非线性谱减
原始的谱减法,只用了一个常数(过减因子)来减去对噪声的过估计。现实世界中的噪声多种多样,可以设置一个频率相关的过减因子来处理不同类型的噪声。
多带谱减法
多带算法,即将语音频域划分N个互不重叠的子带,将谱减法在每个子带独立运行。这个过程有两种方法实践:
- 在时域使用带通滤波器
- 在频域使用适当的窗(推荐:因为实现起来有更小的运算量)
多带谱减与非线性谱减的主要区别在于对过减因子a的估计。非线性谱减算法针对每一个频点,导致频点上的信噪比可能有很大变化,剧烈变化是导致音乐噪声的重要原因。而多带算法针对频带估计减法因子,故子带信噪比变化不会特别剧烈。
MMSE谱减算法
上面的方法中,谱减参数a和b通过实验确定,无论如何都不会是最优的选择。
MMSE谱减法能够在均方意义下最优地选择谱减参数。具体请参考论文:《A parametic formulation of the generalized spectral subtractor method》
扩展谱减法(可以试着实践)
基于自适应维纳滤波与谱减原理的结合。维纳滤波用于估计噪声谱,然后从带噪语音信号中减去该噪声谱。具体请参考以下两篇论文:
《Extended Spectral Substraction:Description and Preliminary Results. 》
《Extended Spectral Substraction》
自适应增益平均的谱减(看不懂)
谱减法中导致音乐噪声的两个因素在于谱估计的大范围变化以及增益函数的不同。对于第一个问题,Gustafsson等人建议将分析帧划分为更换小的子帧以得到更低分辨率的频谱。子帧频谱通过连续平均以减小频谱的波动。对于第二个问题Gustafsson等人提出使用自适应指数平均,在时间上对增益函数做平滑。此外,为了避免因使用零相位增益函数导致的非因果滤波问题,Gustafsson等人建议在增益函数中引入线性相位。具体请参考论文:Spectral subtraction using reduced delay convolution and adaptive averaging
选择性谱减法(待细看)
前面提到的方法对所有语音都做同样处理。并不区分是浊音段还是清音段。区分浊音与清音的谱减法有
- 双频带谱减法。通过将带噪语音能量与某一阈值进行比较,把语音帧分为浊音和清音。对于浊音帧,用算法确定一个截止频率,在该截止频率之上,语音被认为是随机信号。浊音段则通过滤波分为两个频带,一个频带位于截止频率之下(低通滤波后的语音),另外一个频带高于截止频率(高通滤波后的语音)。然后对低通和高通后的语音信号使用不同的算法进行处理。对低通语音部分在短时傅立叶变换的基础上使用过减算法,对于高通部分以及清音段,使用Thomson的多窗谱估计器取代FFT估计器。主要目的在于减小高频部分的频谱值的波动。具体请参考论文:Adaptive two-band spectral subtraction with multi-window spectral estimation
- 双激励语音模型法,该算法把语音分为两个独立的组成部分–浊音分量和清音分量。也就是说,语音由这两个分量的和来表示(注意不同于将语音分为浊音段和清音段)。浊音分量的分析是基于对基音频率和谐波幅度的提取。然后从带噪语音谱中减去浊音谱就得到了清音谱。然后使用一个双通道系统,基中一个包括改进的维纳滤波器,被用于增强清音谱。最终增强的语音由增强后的浊音分量和清音分量求和得到。具体请参考论文:Speech enhancement using the dual excitation speech model
- 还有一种基于浊音、清音的谱减算法,在该算法中语音帧首先根据能量和过零率被划分为浊音和清音。然后将带噪语音谱与锐化函数进行卷积,清音的频谱就会被锐化(用锐化函数进行镨锐化的目的在于增加谱对比度,即在抑制谱谷的同时使谱峰更加突出)。具体请参考论文:Spectral subtraction based on phonetic dependency and masking effects
基于感知特性的谱减(这个可以有)
前面提到的方法,谱减参数要么是通过实验计算短时信噪比得到,要么是通过最优均方误差得到,均没有考虑听觉系统的特性,该算法的主要目的是使残余噪声在听觉上难以被察觉。利用了人类听觉系统改进系统的可懂度(即人耳的掩蔽效应)