噪声测试实验

环境说明：

• 100作为背景UBM测试量

• 50作为测试数据集，取前1句话作为训练，后9句话测试

• 噪声部分：噪声类型：白噪声【SNR=20】

• GMM测试最优组合：Nmix=32~64，MFCC_conf = 'E'

倒谱均值减（倒谱均值归一化）实验测试

之前已经分析过：噪声会影响到倒谱的统计量，有效的做法就是讲倒谱的均值去除（归一化）能减少噪声对语音归一化后的倒谱的影响。但是估计倒谱的方式很多，这里尝试以下几种倒谱估计方法。

1. 【CMS_by_frame】倒谱均值：每一句话计算一个倒谱均值

2. 【CMS_by_frame】倒谱均值：根据每一个人每一句话计算倒谱均值。

   • 去除一阶统计量：即均值
   • 去除二阶统计量：即方差

3. 【CMS_by_people】倒谱均值：将10句话累加起来，计算一个倒谱均值

   • 去除一阶统计量：即均值
   • 去除二阶统计量：即方差

4. 【CMS_by_formuls】根据论文中给出的倒谱估计公式：

   $\mathbf{m}(t)=\left\{\begin{array}{ll} \lambda \cdot \sum_{i=1}^{N}(\mathbf{C}(i) / N)+(1-\lambda) \cdot \mathbf{C}(t+N) & t=1 \\ \lambda \cdot \mathbf{m}(t-1)+(1-\lambda) \cdot \mathbf{C}(t+N) & 2 \leq t \leq T-N \\ \mathbf{m}(T-N) & T-N<t \leq T \end{array}\right.$

   其中N是计算倒谱均值m窗宽，$\lambda$ 是更新步长，两者满足：

   $1-\lambda^{N} = \frac{1}{\sqrt{2}}$

根据经过测试发现：

• 若N取一个固定值，最优值为100，
• 当N取动态长度时，最优值值是：当前语音测试段的一半帧长。

使用方法	SNR=40	SNR=20	SNR=0
未倒谱改进	89.111111%	69.333333%	29.555556%
CMS_by_frame	73.111111%	54.666667%	21.111111%
CMVS_by_frame	66.222222%	47.111111%	18.888889%
CMS_by_people	83.333333%	61.777778%	11.777778%
CMVS_by_people	90.000000%	73.777778%	16.888889%
CMS_by_formuls	82.000000%	65.777778%	31.777778%

结论：

• 以一句话计算的倒谱均值，识别率整体不高，可以pass掉
• 以10句话计算的倒谱均值，在低噪环境中有优势
• 以论文中给的给出的倒谱均值公式，在低信噪比的环境中有优势。

i-vector + lda/plda

实验环境太复杂，只看识别率相对比较值

实验1：验证i-vector是否在有噪环境下比GMM-UBM表现更好？

nmix	64	128	512	1024
GMM-UBM	77.6%	81.6%	77.2%	76%
i-vector+余弦距离	56%	64%	70.8%	64%
i-vector+lda+余弦距离	78%左右	82%左右	84.4%左右	77%左右
i-vector是否有优势	水平相当	水平相当	有一点优势	水平相当

结论：

• 随着Nmix的提高，传统的GMM-UBM的识别率已经到达瓶颈了，再提高只会消耗计算性能。
• 不降维的i-vector如果直接计算余弦距离，识别结果不是好高。
• i-vector-lda算法中自带降维思想，所以维数越高表现越明显，已经很多组实验验证了这个趋势。

实验2：与实验1作对比实验，实验条件为：无噪环境

nmix	32	64	128	256	512
GMM-UBM	91	90	85.5555556	85.5555556	80.88888
i-vector+ 余弦距离	48.88888	66	74.88888	74.66666	76.444444
i-vector+lda+余弦距离	82左右	82左右	84左右	88左右	85左右
i-vector是否有优势	差	差	相当	稍高	高

实验结论：

• 在无噪环境下，i-vector在相同nmix下，某些场景确实好于GMM-UBM算法
• 但是GMM-UBM在nmix=32，能用更少的计算量达到最好的全局最优识别率，所以在无噪环境下GMM-UBM优势更大。

实验1与实验2的比较结论：

• 无噪环境：GMM-UBM表现更好。
• 有噪环境：i-vector + lda 稍好，能体现一定优势。

实验3：进行更为细致的信道测试

nmix	GMM-UBM	噪声类型	i-vector	i-vector+lda	i-vector是否有优势
64	81.555555	car	53.333333	75左右	差
256	78.444444	car	68	78左右	相当
512	77.333333	car	70	78左右	略好
1024	77.111111	car	65.333333	75左右	相当
32	71.777778	cafe	31.777777	60左右	差很多
64	69.333333	cafe	44.666666	67左右	略差
512	55.333333	cafe	512.55555	65左右	好很多
1024	53.111111	cafe	49.777778	60左右	好些
32	62.8888889	white	22	50左右	差很多
64	61.5555555	white	32.444444	60左右	相当
512	55.3333333	white	51.555556	65左右	好很多
1024	53.1111111	white	49.777778	60左右	略好

实验结论：

• car环境下：GMM-UBM优于i-vector
• cafe环境下：GMM-UBM优于i-vector
• white环境下：i-vector优于GMM—UBM，（白噪声对识别率的影响更大）

实验4：i-vector+PLDA测试：

识别部分公式：

$\begin{aligned} \text { score } &=\log \mathcal{N}\left(\left[\begin{array}{l} \eta_{1} \\ \eta_{2} \end{array}\right] ;\left[\begin{array}{l} m \\ m \end{array}\right],\left[\begin{array}{ll} \Sigma_{t o t} & \Sigma_{a c} \\ \Sigma_{a c} & \Sigma_{t o c} \end{array}\right]\right) \\ &-\log \mathcal{N}\left(\left[\begin{array}{l} \eta_{1} \\ \eta_{2} \end{array}\right] ;\left[\begin{array}{l} m \\ m \end{array}\right],\left[\begin{array}{cc} \Sigma_{t o t} & 0 \\ 0 & \Sigma_{t o t} \end{array}\right]\right) \end{aligned}$

模型矢量和测试矢量来自一个分布的概率 减去 模型矢量和测试矢量来自不同分布的概率。这部分MSR工具箱已经有现成的代码了。而且主要被应用于说话人确认系统中。

自编公式：

${p\left(\mathbf{u}^{p} | \mathbf{u}_{1, \ldots, n}^{g}\right)=\mathcal{N}\left(\frac{n \Psi}{n \Psi+I} \overline{\mathbf{u}}^{g}, \frac{\Psi}{n \Psi+I}+I\right)} \\$

测试向量在原空间分下的概率为多少，概率越大则判定为所属分类，更加直观。

训练时长	是否加噪	GMM-UBM	i-vector+余弦	lda降噪	1v1公式	自编函数
1	无噪	80.888889	78.888889	88.444444	70.666667	72.444444
2	无噪	92.75	91	94	93	93.5
3	无噪	91.714286	95.428571	96.571429	94.571429	94.857143
1	有噪	26	16.22222	32	28.888889	28.222222
3	有噪	34.571429	19.428571	50	48.571429	46.857143
5	有噪	44.4	20	59.2	57.6	59.2
5	强信道	27.2	6.8	45.2	41.2	42

实验结论：

• i-vector+plda没有明显优势，识别率相较于lda降噪结果略低，且是在lda降噪结果的基础上改进，也就是起的反作用？所以是使用场景的问题？
• i-vector+lda 在强噪环境下优势明显，这里的强信道指的是训练段与测试端加的噪声类型不同。
• 在无噪环境下，训练语音段的增加对于i-vector的作用要高于GMM-UBM。

自适应滤波实验

无噪环境下GMM-UBM的识别率为：90.000000%

测试方法	SNR=10（white噪声）
GMM-UBM	54.888889%
LMS算法(随机截取一段作为input信号)	无法实现
LMS算法(自编)	81.777778%（mu=32，step=10）
LMS算法(调用)	75.555556%（mu=32，step=10）
NLMS算法	87.555556%
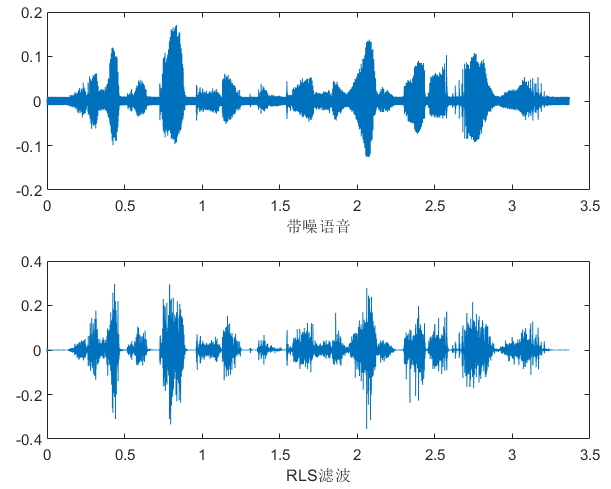
RLS算法	62.000000%

实验结论：

• LMS 有个缺点是：不容易收敛，理论上NLMS能解决这种收敛迭代问题

• RLS：计算量巨大，理论上能快速收敛，通过实际观察波形图，确实前面一段语音噪声没了，但是相对于LMS算法对原波形的影响较大。应该是超参数没有设置到位导致的过渡的去噪。

• 自适应的缺点：必须事先知道噪声类型（这里的实验必须是同时采集信号与噪声两个信息才可以去噪，只知道噪声类型还无法做到比较好的优化）才能得到比较好的优化，理论上解决白噪声的能力优于其他噪声。