数字信号处理–FIR的线性相位特性
1. 什么是线性相位?
经过具有线性相位的离散时间系统H(ejw)后的信号y(n)与原信号x(n)在时域上只存在平移的区别,而非失真。故线性相位对于语音合成、波形传输都是十分重要的。
这里我们只考虑H(ejw)对相位的影响,而不考虑幅值的影响:
{∣H(ejw)∣=1arg[H(ejw)]=−kw
证明:在频域上线性相位 ∼ 时域上平移
Y(ejw)==H(ejw)X(ejw)=ej(−kw)∣X(ejw)∣ejarg[H(ejw)]∣X(ejw∣ej(arg[X(ejw)]−kw)
已知频域与时域的关系为:e−jw ∼ z−1 ∼ x(n−1)
故有:
y(n)=x(n−k)
2. 线性相位的特性
在实际数字系统中,不存在零相频响应的系统,因为其要求系统的单位抽样响应应满足:
h(n)=h(−n),n=0,1,…,N−1
这个显然是非因果系统,即物理不可实现,当然对于非实时信号处理,则可以有这一部分。
3. FIR线性相位系统的设计
FIR为全零点系统,其单位抽样响应为有限长,所以可以实现对h(n)的对称。
-
当h(n)偶堆成时,相位延迟
arg[H(ejw)]=φ(w)=−2N−1w
-
当h(n)偶堆成时,相位延迟
arg[H(ejw)]=φ(w)=−2N−1w+2π
3.1 当h(n)为偶对称
无论N为奇数还是偶数,头尾两两总可以合成一个余弦信号cos
- 若N为奇数,中间的三个点分别为:2N−3,2N−1,2N+1
故有:
H(ejw)===n=0∑N−1h(n)e−jwnn=0∑(N−3)/2j(n)e−jwn+h(2N−1)e−jw⋅2N−1+(N+1)/2∑(N−1j(n)e−jwne−jw⋅2N−1⎩⎨⎧h(2N−1)+2n=1∑(N−1)/2h(2N−1−n)cos(wn)⎭⎬⎫
其中h(2N−1)以及h(2N−1−n)都是常数,统一用a(n)序列表述:
H(ejw)=e−jw⋅2N−1n=0∑(N−1)/2a(n)cos(wn)
可以发现第二部分∑n=0(N−1)/2a(n)cos(wn)是实数,不会影响相位,只会影响幅值。
H(ejw)具有线性相位:
arg[H(ejw)]=φ(w)=−2N−1w
- 若N为偶数,中间的两个点分别为:2N−1,2N
故有:
H(ejw)===n=0∑N−1h(n)e−jwnn=0∑N/2−1j(n)e−jwn+0+N/2∑N−1j(n)e−jwne−jw⋅2N−1n=0∑N/2−12h(2N−n)cos[(n−21)w]
其中h(2N−n)是一个常数,这里用b(n)序列进行表述:
H(ejw)=e−jw⋅2N−1n=0∑N/2b(n)cos[(n−21)w]
同理,上述离散序列系统不会影响相位,只会影响幅值。
H(ejw)具有线性相位:
arg[H(ejw)]=φ(w)=−2N−1w
3.2 当h(n)为奇对称
无论N为奇数还是偶数,头尾两两总可以合成一个余弦信号sin
- 若N为奇数,中间的三个点分别为:2N−3,2N−1,2N+1
故有:
H(ejw)==n=0∑N−1h(n)e−jwnn=0∑(N−3)/2j(n)e−jwn+h(2N−1)e−jw⋅2N−1+(N+1)/2∑N−1j(n)e−jwn
其中,h(n)是奇对称,即h(2N−1)=0,进一步简化为:
H(ejw)=ej(2π−2N−1w)n=1∑(N−1)/2c(n)sin(nw)
H(ejw)具有线性相位:
arg[H(ejw)]=φ(w)=−2N−1w+2π
- 若N为偶数,中间的两个点分别为:2N−1,2N
故有:
H(ejw)==n=0∑N−1h(n)e−jwnn=0∑N/2−1j(n)e−jwn+0+N/2∑N−1j(n)e−jwn
其中,h(n)是奇对称,即h(2N−1)=0,进一步简化为:
H(ejw)=ej(2π−2N−1w)n=1∑N/2d(n)sin[(n−21)w]
具有线性相位:
arg[H(ejw)]=φ(w)=−2N−1w+2π
根据h(n)的不同的类型,可以分类四种I,II,III,IV滤波器。
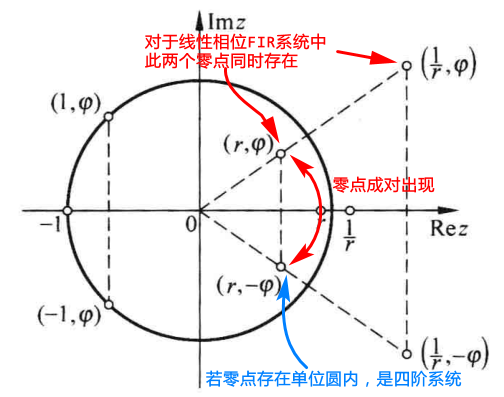
4.具有线性相位特征的FIR系统的零点分布
具有线性相位特征的FIR系统 → h(n)必须奇(偶)对称 → H(z)=±z−(N−1)H(z−1)
综上可知:H(z−1)的零点也是H(z)的零点。
故【线性相位】FIR系统中零点满足:镜像对称
![]()