数字信号处理–全通系统与最小相位系统

全通系统

全通系统的定义

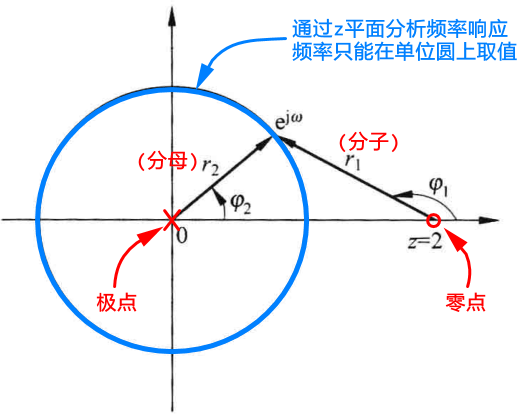
定义：是指不改变信号幅度谱，只改变相位谱的信号处理系统，即

$|H(e^{jw})| = 1 , 0 \le |w| < \pi$

根据 Z变换之极零分析这一节中,已知系统对幅值的影响：

$|H(e^{jw})| = g \frac{\prod_{r=1}^M|e^{jw}-z_r|}{\prod_{r=1}^N|e^{jw}-p_k|}$

所以为了满足$|H(e^{jw})|=1$这个条件，有几种方法

• 零点在圆心，即

  $H(z) = z ^{-k}$

• 若零点不在圆心，需要关于单位圆的镜像对称极点，即

  $H(z) = \frac{1-\lambda^{-1}z^{-1}}{1-\lambda z^{-1}} ,|\lambda|<1$

  易证：

  • 幅频响应：

  $|H(z)|^2 = H(z)H(z^{-1}) =\frac{1-\lambda^{-1}z^{-1}}{1-\lambda z^{-1}} \cdot \frac{1-\lambda^{-1}z}{1-\lambda z} =\lambda^{-2}$

  • 相频响应：

    $arg[H(e^{jw})] = arctan[\frac{-(\lambda - \lambda^{-1})sinw}{2-(\lambda+\lambda^{-1})cosw}]$

    可以看出全通系统必为：$IIR$ 系统

全通系统的性质

• 全通系统是$IIR$系统
• 极点数 = 零点数
• 极点必须在单位圆内，系统才能保持稳定
• 极点和零点是以单位圆镜像对称的
• IIR系统无法做到线性相位

全通系统的应用实例

具体Matlab编程示例见 Z变换之极零分析

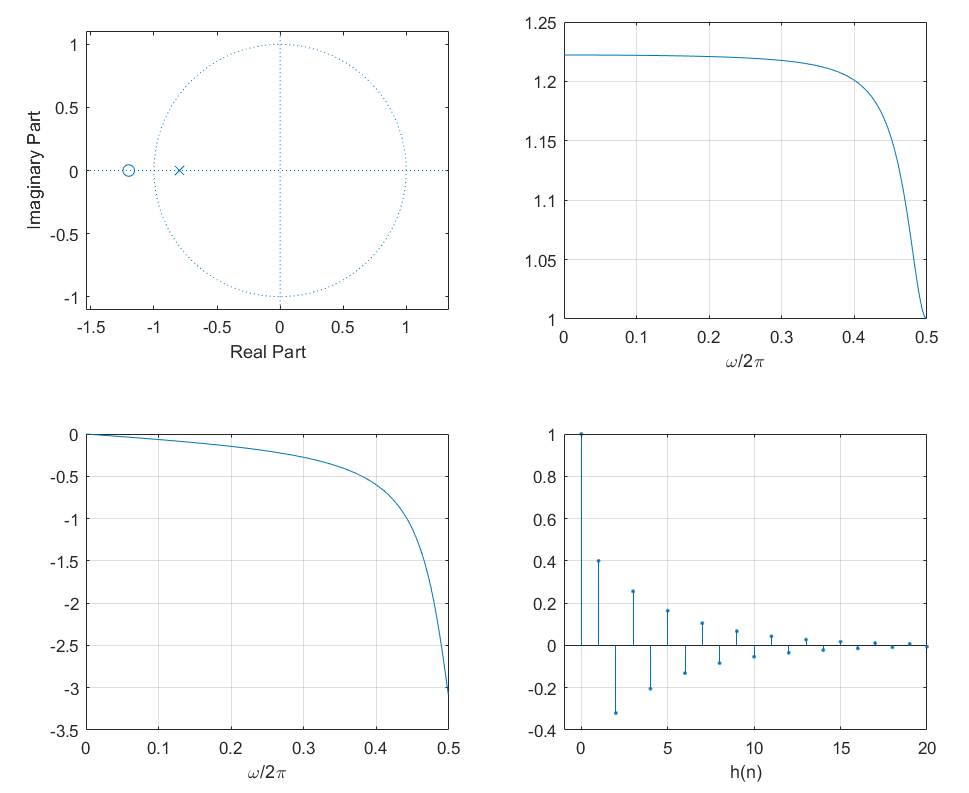
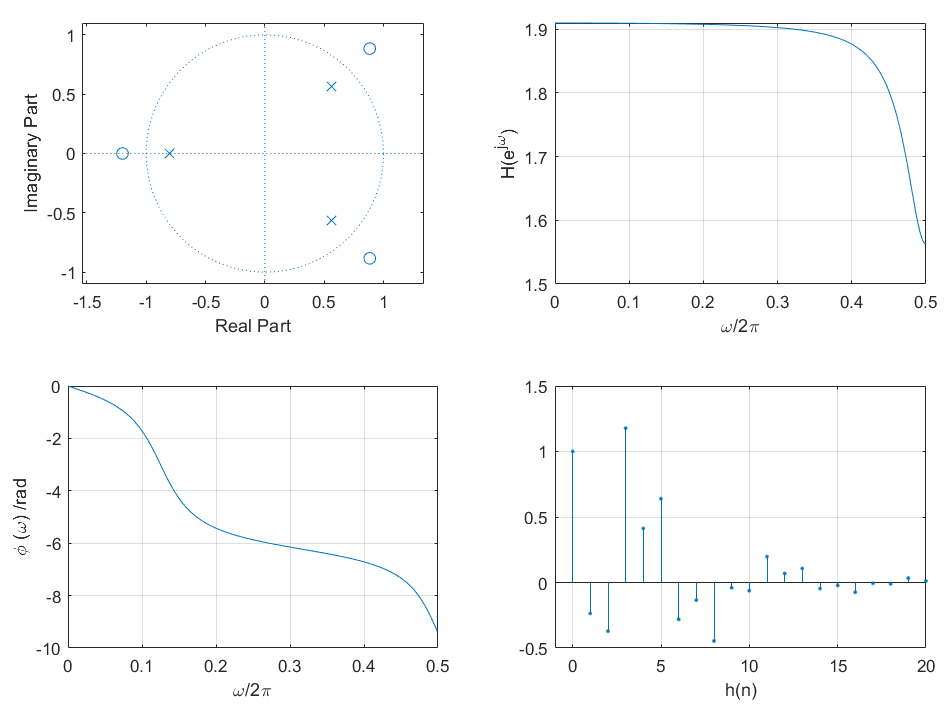
例题 5.4.1 一阶和三阶全通滤波器，画出对应的极零图、幅频响应、相频响应和单位抽样响应。

图一中，极点$p_1 = -0.8$，零点$z_1= -1.2$。图二中，极点为$0.8e^{j\pi/4},0.8e^{-j\pi/4}$及-0.8。对应的零点为单位圆对称位置，观察图二可知。

Matlab代码：

%% 一阶全通系统
z = -1.2 ;p = -0.8;
[b,a] = zp2tf(z,p,1);
subplot 221;zplane(b,a);
subplot 222;[H,w] = freqz(b,a);Hr = abs(H);
Hphase = angle(H);Hphase = unwrap(Hphase);plot(w/(2*pi),Hr);
grid on;xlim([0,0.5]);xlabel('\omega/2\pi')
subplot 223;plot(w/(2*pi),Hphase);
grid on;xlim([0,0.5]);xlabel('\omega/2\pi')
subplot 224;[h,t] = impz(b,a,40);stem(t,h,'.');
grid on;xlim([-1,20]);xlabel('h(n)')
set(gcf,'color','w')

%% 三阶全通系统
p = [-0.8;0.8*(cos(pi/4)+1i*sin(pi/4));0.8*(cos(pi/4)-1i*sin(pi/4))];
z = [-1.2;(1/0.8)*(cos(pi/4)+1i*sin(pi/4));(1/0.8)*(cos(pi/4)-1i*sin(pi/4))];

[b,a] = zp2tf(z,p,1);
subplot 221;zplane(b,a);
subplot 222;[H,w] = freqz(b,a);Hr = abs(H);
Hphase = angle(H);Hphase = unwrap(Hphase);plot(w/(2*pi),Hr);
grid on;xlim([0,0.5]);xlabel('\omega/2\pi');ylabel('H(e^{j\omega})');
subplot 223;plot(w/(2*pi),Hphase);
grid on;xlim([0,0.5]);xlabel('\omega/2\pi');ylabel('\phi (\omega) /rad');
subplot 224;[h,t] = impz(b,a,40);stem(t,h,'.');
grid on;xlim([-1,20]);xlabel('h(n)')
set(gcf,'color','w')