数字信号处理 – Z 变换
Z变换是离散系统与离散信号分析与综合的重要工具,其地位和作用犹如拉普拉斯对于连续系统和连续信号。
从连续信号过渡到离散信号会导致频谱产生周期性,所以连续信号与离散信号存在本质性区别。
什么是Z变换?
Z变换的定义,根据《数字信号处理》这本书,可以从两个角度导出:
1. 直接对离散信号定义
对离散信号x(n),n=−∞∼+∞,可直接给出x(n)的Z变换的定义:
X(z)=n=−∞∑∞x(n)z−n
又,实际信号是因果的
X(z)=n=0∑∞x(n)z−n
2. 从连续信号导出
这里的目的是为了解释实际连续信号圆频率Ω ,归一频率f′,离散信号圆周频率w 之间的关系。
对【采样后】连续信号进行拉普拉斯变换:
X(s)=∫−∞+∞x(nTs)e−stdt=n=−∞∑∞x(nTs)e−snTs
令z=esTs 【可以发现 s 与 z 是一一对应的】,也可得到Z变换的定义式
X(z)=n=−∞∑∞x(n)z−n
通过以上的分析,就将连续信号与离散信号联系了起来:
z=esTs
3. 离散信号x(n)的含义
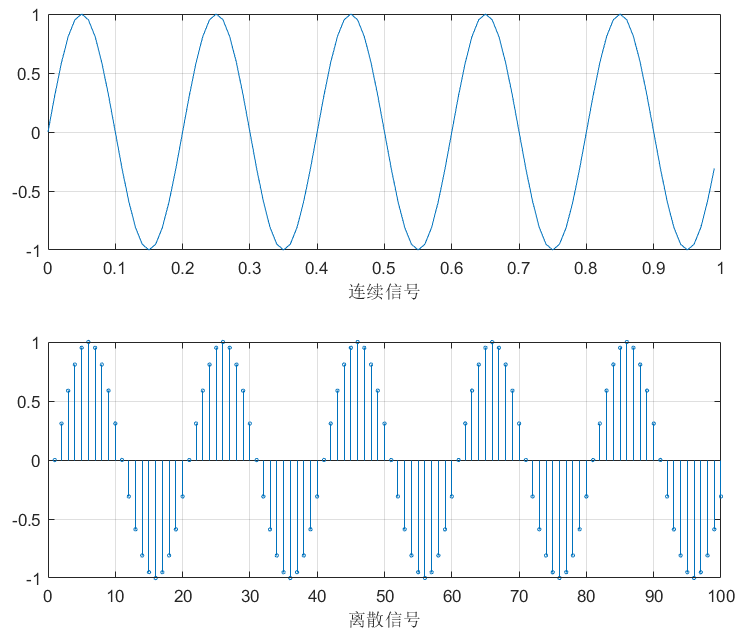
离散信号x(n)是从连续信号x(t)中采样出来的,这个时候就有个疑问,离散信号的n与t有什么关系呢?
离散信号x(n)是连续信号采样x(nTs)的简写。
![]()
3.真频率与"假"频率
我这里将真频率定义为连续信号中的频率,假频率是经过采样后的离散信号中的频率。真频率的单位就是Hz,假频率是将真频率根据采样频率fs归一化得到的,反映的是一种比值,单位无量纲。
拉普拉斯复变量:s=σ+jΩ
Z复变量:
z=esTs=e(σ+jΩ)Ts=∣z∣ejw
拉普拉斯变换【实际连续频率Ω】与Z变换【离散信号频率w】的关系:
ω=ΩTs=2πf/fs=2πf′
真频率与假频率的关系:
![]()
4. 拉普拉斯变换、Z变换与DFT变换的联系
傅里叶变换:
X(ejw)=n=−∞∑∞x(n)e−jwn
Z 变换:
X(z)=n=−∞∑∞x(n)z−n
将z=esTs=∣z∣ejw 代入Z变换公式中,
X(∣z∣ejw)=n=−∞∑∞[x(n)∣z∣−n]e−jwn
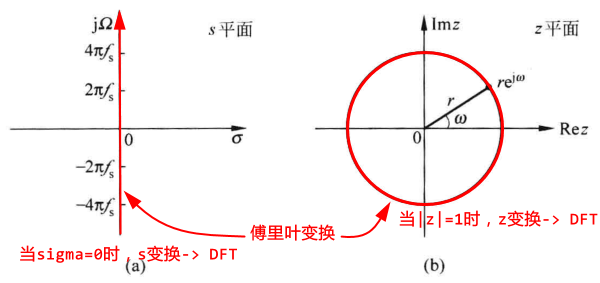
当∣z∣=1时(也即σ=0时),Z变换→ 离散序列傅里叶变换
X(z)∣z=ejw=X(ejw)=n=−∞∑∞x(n)e−jwn
s平面与z平面下的傅里叶变换:
![]()
注:S平面是直角坐标系,Z平面是极坐标系。可以发现在S平面与Z平面都可以转换为傅里叶变换。
Z 变换的收敛域
这里主要就是用到了幂级数的收敛,
例:x(n)=anu(n) ,其中u(n)是单位阶跃函数,求x(n)的Z变换并决定收敛域。
X(z)=n=−∞∑∞anu(n)z−n=n=0∑∞(az−1)n
要使得Z变换有意义,那么变换所得的函数必须在有限处收敛
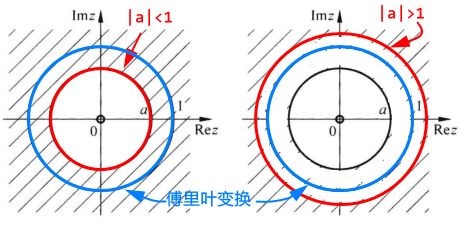
∣az−1∣<1
则,当∣Z∣>∣a∣时,级数收敛:
X(z)=1−az−11=z−az
![]()
Z变换的实例
考虑一个为两个实指数和的信号
x[n]=(21)nu[n]+(−31)nu[n]
其Z变换为:
X(z)=n=−∞∑∞{(21)nu[n]+(−31)nu[n]}z−n=n=−∞∑∞(21)nu[n]z−n+n=−∞∑∞(−31)nu[n]z−n=n=0∑∞(21z−1)n+n=0∑∞(−31z−1)n=1−21z−11+1+31z−11 Geometric Series =(z−21)(z+31)2z(z−121)
为了使Z变换收敛,必须满足条件:
{∣∣21z−1∣∣∣∣−31z−1∣∣<<11
即
{∣z∣∣z∣>>2131
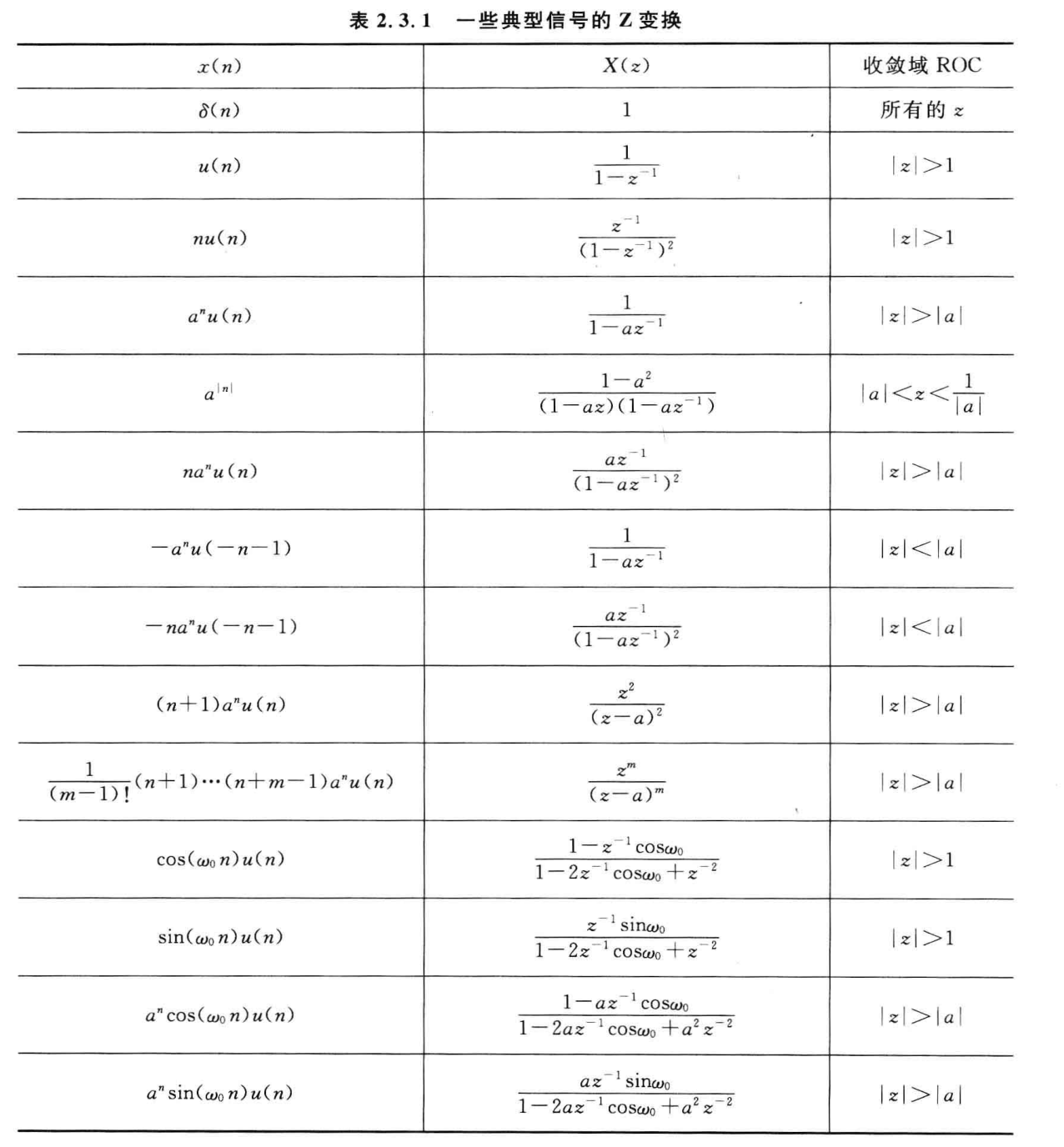
常用信号 Z变换
![]()
参考资料
- https://www.cnblogs.com/TaigaCon/p/8299433.html
- 《数字信号处理》(第3版)