数字信号处理–功率谱估计
前言
之前学习谱减法的时候,就遇到了有关谱估计的内容,比如在SSBoll79.m中有YS(:,i)=(Y(:,i-1)+Y(:,i)+Y(:,i+1))/3;这样的语句不是很理解,代码的注解是为了减少功率谱的方差,因为遗忘掉了这部分的内容所以看得一知半解,现在对胡广书版的《数字信号处理》的第13章经典功率谱估计做个复习。
已复习章节:
- 数字信号处理–随机信号与随机变量
- 数字信号处理–相关函数
本篇应用章节:
自相关函数的估计
在讲功率谱估计之前,需要先介绍自相关函数的估计,原因是x2N(n)功率谱[直接法功率谱]与自相关函数r^(m)是一对傅里叶变换。所以,可以通过自相关函数间接地对功率谱进行估计,即间接法。
广义平稳随机信号X(n)自相关函数的定义,(建立在集总平均的基础上):
rX(m)=E{X∗(n)X(n+m)}
根据《数字信号处理–随机信号与随机变量》那一章,各态遍历:时间平均=集总平均,可有:
r(m)=N→∞lim2N+11n=−N∑Nx∗(n)x(n+m)
又因,实际信号是因果且实信号:
r(m)=N→∞limN1n=0∑Nx(n)x(n+m)
又,极限在实际上又无法做到,去极限:
r^(m)=N1n=0∑Nx(n)x(n+m)
观察上述第二项x(n+m)是时延m,原先数学原理上N是取无穷的,故上式中m是可以取到N的,但是在实际运算中,给到我们的x(n)只有N个观察值。故数据只能取到N−∣m∣个。
故实际编程中:
-
有偏估计biased
r^(m)=N1n=0∑N−1−∣m∣xN(n)xN(n+m)
-
无偏估计unbiased
r^(m)=N−∣m∣1n=0∑N−1−∣m∣xN(n)xN(n+m)
傅里叶变换对–相关函数&功率谱
这里主要介绍:如何快递计算自相关函数【FFT方法】
为什么有这一章节呢?
需证:x2N(n)功率谱与自相关函数r^(m)是一对傅里叶变换
m=−(N−1)∑N−1r^(m)e−jwm=N1∣∣X2N(ejw)∣∣2
证:
-
相关函数定义:
r^(m)=N1n=0∑Nx(n)x(n+m)
-
对r^(m)求傅里叶变换
m=−(N−1)∑N−1r^(m)e−jwm=N1m=−(N−1)∑N−1n=0∑N−1xN(n)xN(n+m)e−jω−=N1n=0∑N−1xN(n)m=−(N−1)∑N−1xN(n+m)e−jωm
-
补零操作
为啥要补零?,观察上式中两项,为了凑出两个DFT,第一项DFT的点数为N点,第二项DFT的点数为2N-1点。为了使最后的结论可以合并,需要让FFT的nfft的点数相同。
x2N(n)={xN(n)0n=0,1,⋯,N−1N⩽n⩽2N−1
-
过程略
m=−(N−1)∑N−1r^(m)e−jwm=N1n=0∑2N−1x2N(n)ejwnl=0∑2N−1x2N(l)e−jwl=N1∣∣X2N(ejw)∣∣2
-
⭐️得证
m=−(N−1)∑N−1r^(m)e−jwm=N1∣∣X2N(ejw)∣∣2
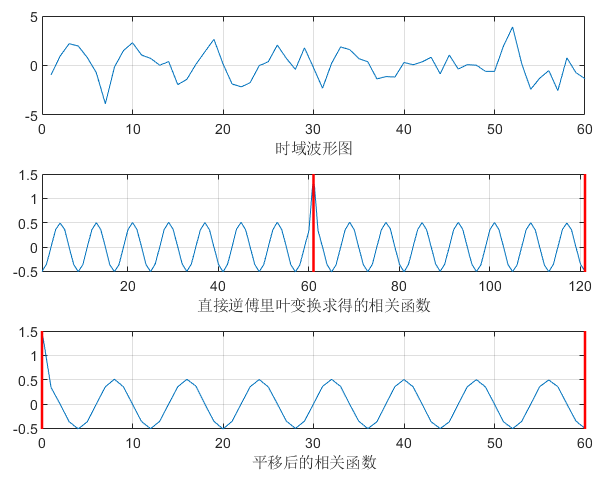
算法流程
-
对xN(n)补N个零,做DFT
-
求X2N(k)的幅平方,除以N,得N1∣X2N(k)∣2
-
做逆傅里叶变换,得r^0(m)
-
平移半个周期,得r^(m)
![相关函数的仿真]()
N = 50000;
p1 = 1;p2 = 0.1;
f = 1/8;
Mlag =60;
u = randn(1,N);
n = 0:N-1;
s = sin(2*pi*f*n);
x1 = u*sqrt(p1) + s ;rx1 = xcorr(x1,Mlag,'biased');
x2 = u*sqrt(p2) + s ;rx2 = xcorr(x2,Mlag,'biased');
subplot 311;plot(1:Mlag,x1(1:Mlag));grid on;xlabel('时域波形图')
subplot 313;plot(0:Mlag,rx1(Mlag+1:end));grid on;xlabel('平移后的相关函数')
ylim([min(rx1),max(rx1)]);
line([0,0],[-10,10],'linewidth',1.5,'color','r');
line([Mlag,Mlag],[-10,10],'linewidth',1.5,'color','r');
subplot 312;plot(rx1);grid on;xlabel('直接逆傅里叶变换求得的相关函数')
ylim([min(rx1),max(rx1)]);xlim([1,length(rx1)]);
line([Mlag+1,Mlag+1],[-10,10],'linewidth',1.5,'color','r')
line([length(rx1),length(rx1)],[-10,10],'linewidth',1.5,'color','r')
set(gcf,'color','w')
|
估计质量分析
有偏自相关函数biased
r^(m)=N1n=0∑N−1−∣m∣xN(n)xN(n+m)
-
偏差
bia[r^(m)]====E{r^(m)}−r(m)N1n=0∑N−1−∣m∣r(m)−r(m)NN−∣m∣r(m)−r(m)−N∣m∣r(m)
得证:有偏
-
方差:当N→∞,得var[r^(m)]→0
无偏自相关函数unbiased
r^(m)=N−∣m∣1n=0∑N−1−∣m∣xN(n)xN(n+m)
-
偏差
bia[r^(m)]===E{r^(m)}−r(m)N−∣m∣1n=0∑N−1−∣m∣r(m)−r(m)r(m)−r(m)=0
-
方差
观察无偏公式可以发现,当随着∣m∣的增大,有效计算的点数变得越来越少,导致其方差性能变坏,因此较少使用。
经典功率谱估计
分类
-
直接法
P^PER(k)=N1∣XN(k)∣2
-
间接法
P^BT(w)=m=−M∑Mr^(m)e−jwm,∣M∣≤N−1
直接法和间接法的关系
已知:N1∣X2N(k)∣2与自相关函数**r^(m)**是一对傅里叶变换。
P^PER2N===N1∣X2N(k)∣2=DFT(r^(m))m=−(N−1)∑N−1r^(m)e−j2N2πmm=−M∑Mr^(m)e−j2N2πm=P^BT2N(k)
以上可以发现当M=N−1时,直接法求功率谱∼间接法求功率谱。
P^PER2N==m=−(N−1)∑N−1r^(m)e−j2N2πmm=−M∑Mr^(m)e−j2N2πm=P^BT2N(k)
若M=N−1时,间接法相当于在直接法的基础上加了个窗
P^BT2N(k)===m=−M∑Mr^(m)e−j2N2πmm=−(N−1)∑N−1r^(m)v(m)e−j2N2πmm=−(N−1)∑N−1r^M(m)e−j2N2πm=P^PER2N(k)∗V(k)
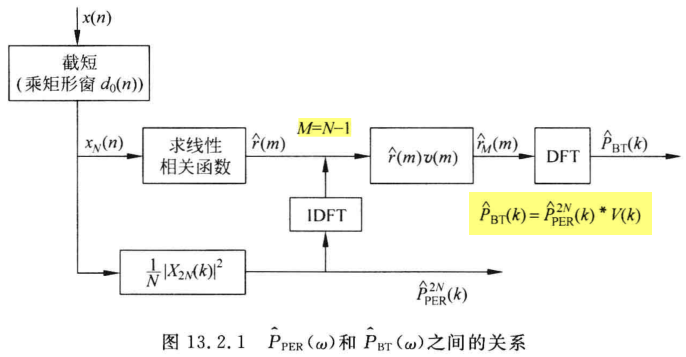
综上,可以总结算法流程图如下:
算法流程图
![算法流程]()
故间接法的优点:
-
计算量少
但是间接法中要求M<<N−1,所以计算量相比直接法小到爆炸,故早期求功率谱大多用的都是间接法。
-
加窗后,谱线更加平滑,即方差更小。
经验总结:
- 如果我们希望找到随机信号是由什么组成的,用直接法求功率谱更好(方差大,即频率分辨率高),比较容易发现正弦信号在频域的位置。
- 若希望用能量谱或者功率谱作为输入函数去训练,如果方差太大,肯定训练结果会很差(未经验证?)。在谱减法中,方差越小有利于减少"音乐噪声"。
- 总体来说,减少方差,有两个思路,平均和平滑
- 时域:对数据进行加窗
- 频域:做卷积操作,卷积本质上就是加权平均(为什么?待补)可以平滑周期图。
直接法和间接法估计的质量
这部分内容,胡广书太学术化了,根本没必要掌握这么深,但是最后的总结写的非常好,无论如何改进周期图,本质就是无法同时保证方差,偏差,分辨率最优,实际工作中根据需求做出折中的选择。
故,这部分内容暂时忽略,有空再补。
直接法估计的改进
直接法估计性能差,当数据长度N太大时,谱曲线起伏家具,N太小时,谱的分辨率又不好。【这个和对数据做FFT有这类似的感受,nfft太小了,基本上看不清频率,同理波动也很小,nfft取太大,就需要对数据进行补零,计算分辨率可以提高(理论分辨率取决于FS)】
主要的改进思路有两种:
- 平均法:把数据xN(n)分为L段,把每一段功率加和平均
- 平滑法:间接法本质上就是平滑,上面已经解释过了原因了。
下面具体介绍三种实践流程:
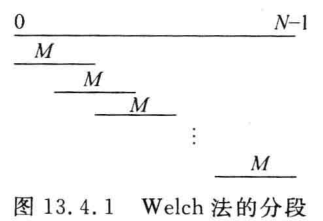
Bartlett法
具体思想:由概率论可知,对L个具有相同的均值μ和方差σ2的独立随机变量X1,X2,…,XL,新随机变量X=(X1+X2+⋯+XL)/L的均值也是μ,但方差是σ2/L为原来的1/L。
Welch法
Welch法是对Bartlett法的改进。改进之一就是,允许数据重叠,在Matlab中通过enframe可以实践。改进二,分帧的时候可以加不同的窗函数(hamming,hanning等)。
Welch法又称加权交叠平均法,应用较广。
![]()
优缺点:
- 各段允许交叠,方差可以改善很多,但是数据交叠减少了每一段的不相关性。
Nuttall法
此方法是同时将**平均(分段求和)+平滑(间接法)**结合起来,双重减少方差,且计算量小于Welch法。
具体实践流程:
- 无重叠分帧,求每段的功率谱,求和取平均。【直接法】
- 直接法求自相关函数
- 给相关函数加窗v(m)
- 根据相关函数r^M(m),可以直接傅里叶正变换。
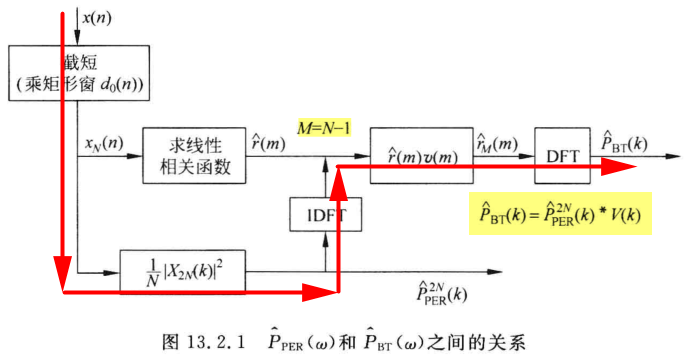
综上,本质上来讲上面的流程very Simple。就是不直接套用间接法公式直接求功率谱,反而绕一大圈通过直接法去求间接法的功率谱。
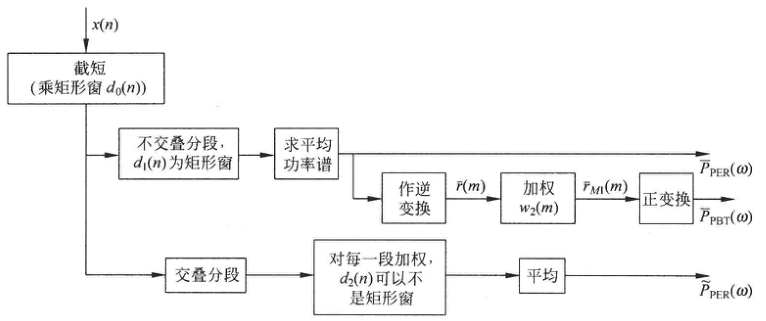
比较与之前的计算流程为:
![]()
PˉPBT的均值为:
E{PˉPBT(w)}=P(w)∗W1(w)∗W2(w)
其中,W1(w)是矩形窗d1(n)所形成的三角频谱,W2(w)是加载在相关函数v(w)所形成的频谱。可以很明显地看出Nuttall法是通过平均和平滑对频谱的影响。
综上:三种改进方法的流程图:
![三种改进方法的框图]()
经典谱估计算法性能的比较
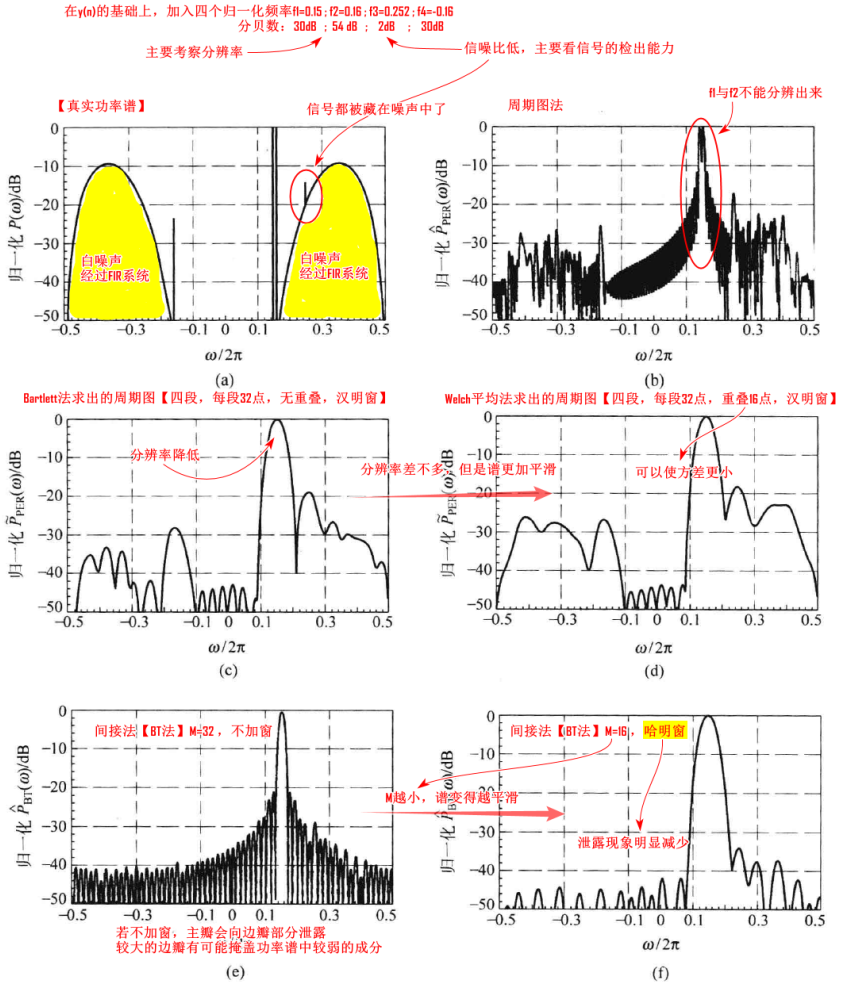
案例:《数字信号处理》
![]()
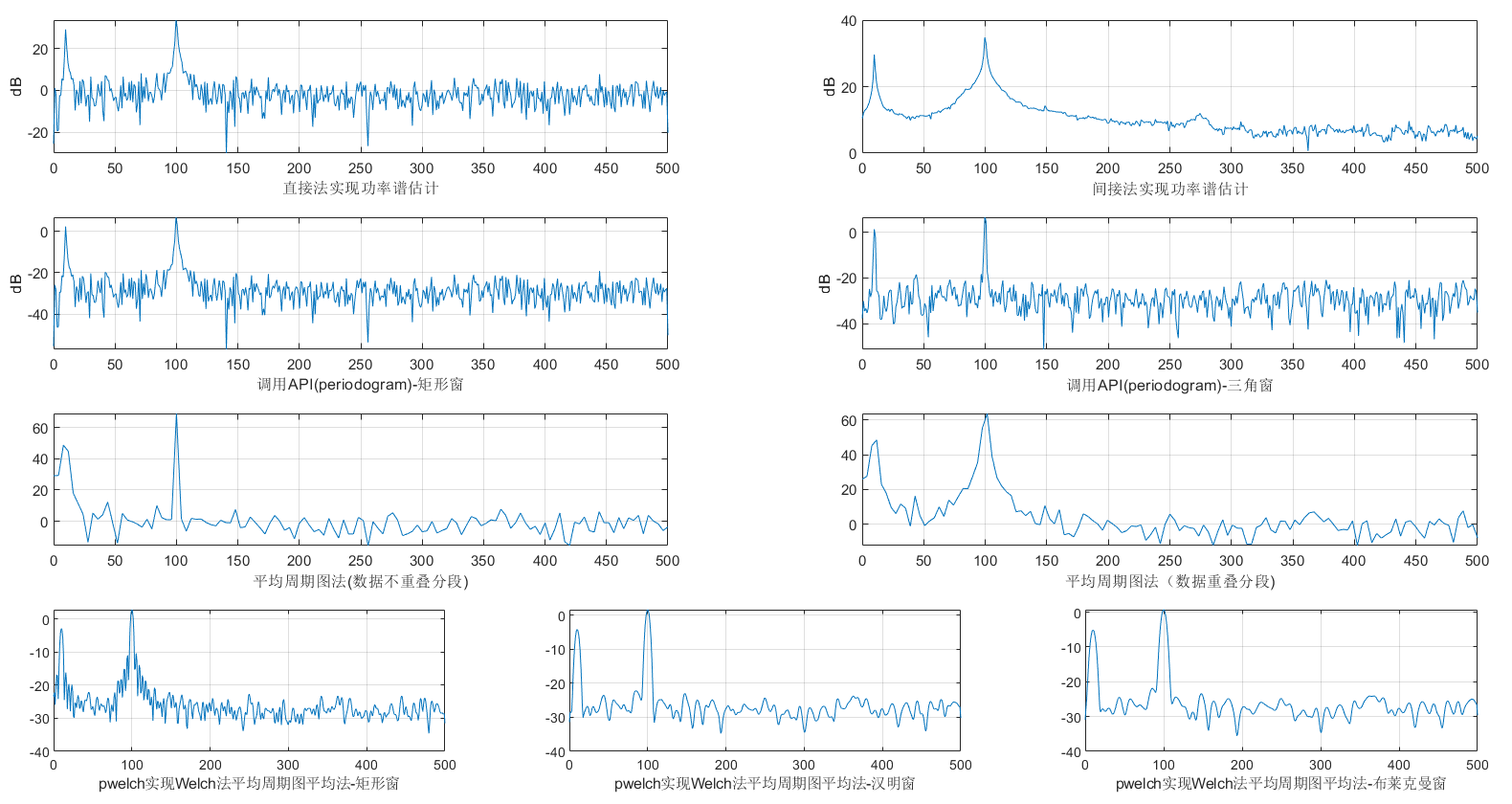
案例:Maltab仿真实践
| 图标 |
方法 |
是否调用API |
总结 |
| (1,1) |
直接法 |
否 |
根据原理自编,可以发现和调用API(periodogram)效果相同,可以看出方差很查,分辨率高。 |
| (2,1) |
直接法 |
是 |
API:periodogram |
| (2,2) |
直接法+加窗 |
是 |
API:periodogram
主要影响旁瓣的大小以及解决泄露问题。 |
| (2,1) |
间接法 |
否 |
方差相对于直接法小很多 |
| (3,1) |
平均周期图法(Bartlett法)【矩形窗】【数据不重叠】 |
否 |
方差下降很明显,肉眼看上去效果不错 |
| (3,2) |
平均周期图法(Welch法)-【矩形窗】-【数据重叠】 |
否 |
效果比非重叠的平均周期图法,略差。 |
| (4,1~3) |
平均周期图法(Welch法)-【数据重叠】 |
是 |
API:pwelch
只要不用矩形窗,方差下降都挺多的。
比较第3行,第2列的图。从理论上,两者效果应相同。可能内部有差异把。 |
![功率谱估计]()
clc;clear;close all
Fs = 1000;
NFFT_2 = 1024;
time = 0:1/Fs:0.999;
freq = linspace(0,Fs/2,NFFT_2/2+1);
noise = randn(1,length(time));
x = 4 * sin(2*pi*100*time) - 2*sin(2*pi*10*time) + noise;
N = length(x);
window = boxcar(N);
[Power1,f1]=periodogram(x,window,NFFT_2,Fs);
Power1_dB = 10*log10(Power1);
window2 = bartlett(N);
[Power2,f2]=periodogram(x,window2,NFFT_2,Fs);
Power2_dB = 10*log10(Power2);
Cx = xcorr(x,'unbiased');
Cxk = fft(Cx,NFFT_2);
Power4 = abs(Cxk);
Power4_dB = 10*log10(Power4) ;
y = fft(x,NFFT_2);
y2 = abs(y);
power = y2.^2/NFFT_2;
power_dB = 10*log10(power);
figure();
subplot 421;plot(freq,power_dB(1:NFFT_2/2+1));
xlabel('直接法实现功率谱估计');ylabel('dB');grid on;
subplot 423;plot(f1,Power1_dB);
xlabel('调用API(periodogram)-矩形窗');ylabel('dB');grid on;
subplot 424;plot(f2,Power2_dB);
xlabel('调用API(periodogram)-三角窗');ylabel('dB');grid on;
subplot 422;plot(freq,Power4_dB(1:NFFT_2/2+1));
xlabel('间接法实现功率谱估计');ylabel('dB');grid on;
set(gcf,'color','w');
NFFT_1 = 250;
Pxx1 = abs(fft(x(1:250),NFFT_1).^2)/NFFT_1;
Pxx2 = abs(fft(x(251:500),NFFT_1).^2)/NFFT_1;
Pxx3 = abs(fft(x(501:750),NFFT_1).^2)/NFFT_1;
Pxx4 = abs(fft(x(751:1000),NFFT_1).^2)/NFFT_1;
Pxx_n_overlap = 10*log((Pxx1+Pxx2+Pxx3+Pxx4)/4);
freq_1 = linspace(0,Fs/2,NFFT_1/2+1);
win = 256;inc=0.5*win;
y=enframe(x,win,inc)';
NFFT_2 = win;
Pxx1 = abs(fft(y(:,1),NFFT_2).^2)/NFFT_2;
Pxx2 = abs(fft(y(:,2),NFFT_2).^2)/NFFT_2;
Pxx3 = abs(fft(y(:,3),NFFT_2).^2)/NFFT_2;
Pxx4 = abs(fft(y(:,4),NFFT_2).^2)/NFFT_2;
Pxx5 = abs(fft(y(:,5),NFFT_2).^2)/NFFT_2;
Pxx6 = abs(fft(y(:,6),NFFT_2).^2)/NFFT_2;
Pxx_overlap = 10*log((Pxx1+Pxx2+Pxx3+Pxx4+Pxx5+Pxx6)/6);
freq_2 = linspace(0,Fs/2,NFFT_2/2+1);
subplot 425 ;plot(freq_1,Pxx_n_overlap(1:NFFT_1/2+1));
grid on;xlabel('平均周期图法(数据不重叠分段)')
subplot 426 ;plot(freq_2,Pxx_overlap(1:NFFT_2/2+1));
grid on;xlabel('平均周期图法(数据重叠分段)')
set(gcf,'color','w')
NFFT = 1024;
win = 256 ;
window1 = boxcar(win);
window2 = hamming(win);
window3 = blackman(win);
noverlap = 20;
[Pxx1,f1]=pwelch(x,window1,noverlap,NFFT,Fs);
[Pxx2,f2]=pwelch(x,window2,noverlap,NFFT,Fs);
[Pxx3,f3]=pwelch(x,window3,noverlap,NFFT,Fs);
PXX1= 10*log10(Pxx1);
PXX2= 10*log10(Pxx2);
PXX3= 10*log10(Pxx3);
subplot(4,3,10);plot(f1,PXX1);
xlabel('pwelch实现Welch法平均周期图平均法-矩形窗');grid on;
subplot(4,3,11);plot(f2,PXX2);
xlabel('pwelch实现Welch法平均周期图平均法-汉明窗');grid on;
subplot(4,3,12);plot(f3,PXX3);
xlabel('pwelch实现Welch法平均周期图平均法-布莱克曼窗');grid on;
set(gcf,'color','w')
|