重读《数字信号处理》，主要想对下册统计数字信号部分进行梳理。因为人发出的语音信号在每次观察下都是随机的，但是有别与一般的随机变量，它加入了时间这个维度。故针对一个随机信号有两个随机因素，时间 $t$ 和样本观察 $n$ 。先好好的分析一波随机变量，再加入时间推广到随机信号。

随机变量

随机变量 $X$ ：描述自然件随机事件

连续值：服从如正态分布等
离散值：服从如二项分布、泊松分布

表达以上分布的方式：分布函数/概率密度/数字特征

均值、均方值、方差、矩

这几个概念讲解的顺序为：

均值
均方值、方差
矩

⭕️均值：

$\mu_{X}=E\{X\}=\int_{-\infty}^{\infty} x p(x) \mathrm{d} x$

⭕️均方值、方差：

$\begin{array}{c}{D_{X}^{2}=E\left\{|X|^{z}\right\}=\int_{-\infty}^{\infty}|x|^{2} p(x) \mathrm{d} x} \\ {\sigma_{X}^{2}=E\left\{\left|X-\mu_{X}\right|^{2}\right\}=\int_{-\infty}^{\infty}\left|x-\mu_{X}\right|^{2} p(x) \mathrm{d} x}\end{array}$

这里可以发现，这两个概念都可以用 $E\{\cdot\}$ 均值去解释。均方值是对所有样本【所有随机事件】的平方求均值，方差是对离中心点的平方求均值。

⭕️引出高阶矩的概念：

定义原点矩：

$\eta_{X}^{n}=E\left\{|X|^{m}\right\}=\int_{\infty}^{\infty}|x|^{m} p(x) \mathrm{d} x$

定义中心矩：

$\gamma_{X}=E\left\{\left|X-\mu_{X}\right|^{m}\right\}=\int_{-\infty}^{\infty}\left|x-\mu_{X}\right|^{m}{p}(x) \mathrm{d} x$

可以很轻易的发现均方值和方差是引入矩定义后 $m=2$ 下的情况。

根据m的大小可以定义，一阶、二阶、三阶、四阶统计量，等

三阶统计量：斜度

$\text { Skew }=E\left\{\left[\frac{X-\mu_{X}}{\sigma_{X}}\right]^{3}\right\}=\frac{1}{\sigma_{X}^{3}} \gamma_{X}^{3}$

四阶统计量：峰度

$\text { Kurtosis }=E\left\{\left[\frac{X-\mu_{x}}{\sigma_{x}}\right]^{4}\right\}-3=\frac{1}{\sigma_{x}^{4}} \gamma_{x}^{4}-3$

上帝视角与样本的关系

因为之前在机器学习中，对一些概念性的理解产生了点误解，频率派和贝叶斯派的区分中，有涉及到上帝视角。

核心在于： $p(x)$ 的求解

若来源于样本的且为离散变量，则可以直接用频率来代替概率计算该值【大数定理】
若来源于假设，离散如二项式分布，连续如正太分布，其各自拥有各自的分布律函数。则 $p(x)$ 与样本无关，我称之为上帝视角或者理想真值，因为当假设分布确定时，则 $p(x)$ 就已经确定了。

多维随机变量

当随机变量 $X$ 拥有 $N$ 维特征：

$X = [X_1,X_2,\dots,X_N]^T$

则均值为：

$\boldsymbol{\mu}_{X}=\left[\mu_{X_{1}}, \mu_{X_{2}}, \cdots, \mu_{X_{N}}\right]^{\mathrm{T}}, \mu_{X_{i}}=E\left\{X_{i}\right\}$

在这里统一用 $X$ 代表随机变量，用 $x$ 代表单个样本

则方差矩阵为：

$\begin{aligned} \boldsymbol{\Sigma}= & E\left\{\left(\boldsymbol{X}-\boldsymbol{\mu}_{X}\right) \cdot\left(\boldsymbol{X}-\boldsymbol{\mu}_{X}\right)^{\mathrm{T}}\right\}\\ =& \left[ \begin{matrix} \sigma _{1}^{2}& cov\left( X_1,X_2 \right)& ...& cov\left( X_1,X_N \right)\\ cov\left( X_2,X_1 \right)& \sigma _{2}^{2}& ...& cov\left( X_2,X_N \right)\\ \vdots& \vdots& \vdots& \vdots\\ cov\left( X_N,X_1 \right)& cov\left( X_N,X_2 \right)& \cdots& \sigma _{N}^{2}\\ \end{matrix} \right] \end{aligned}$

不同维度之间的计算用协方差定义的，这里的 $cov(X_i,X_j)$ 最终得到的是实数。

协方差，不仅不同维度之间可以计算，也可扩展成两个多维随机变量之间的定义，此时结果就不再是实数了，而是协方差矩阵。 $cov(X,Y)=E\{(X-\mu_X)(Y-\mu_Y)^T\}$

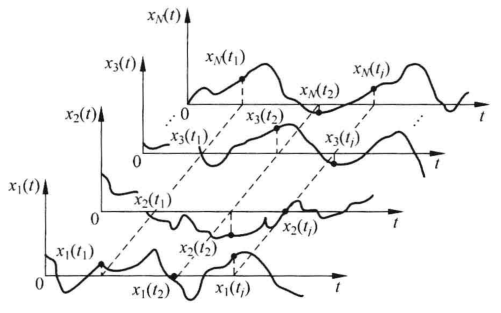
随机信号

这里温漂电压是一个随机信号。在相同的条件下独立地进行多次观察。

随机信号 $x(n,i)$ 有以下四种情况：

若 $n$ 固定（时间固定）， $i$ 变动，则为随机变量
若 $i$ 固定（单样本）， $n$ 变动，则为一个一维离散时间序列
若 $i$ 和 $n$ 都变动，则 $x(n,i)$ 是一个随机信号。
若 $i$ 和 $n$ 都固定，则 $x(n,i)$ 是一个实数。

对随机变量，即样本 $i$ 变动，可做如下统计变量【集总平均】：

均值

$\mu_{X}(n)=E\{X(n)\}=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N} x(n, i)$
方差

$\sigma_{x}^{2}(n)=E\left\{\left|X(n)-\mu_{X}(n)\right|^{2}\right\}=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N}\left|x(n, i)-\mu_{X}(n)\right|^{2}$
均方

$D_{X}^{2}(n)=E\left\{|X(n)|^{2}\right\}=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N}|x(n, i)|^{2}$
自相关函数

$r_{X}\left(n_{1}, n_{2}\right)=E\left\{X^{*}\left(n_{1}\right) X\left(n_{2}\right)\right\}=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N} x^{*}\left(n_{1}, i\right) x\left(n_{2}, i\right)$
自协方差函数

$\begin{aligned} \operatorname{cov}_{X}\left(n_{1}, n_{2}\right) &=E\left\{\left[X\left(n_{1}\right)-\mu_{X}\left(n_{1}\right)\right] \cdot\left[X\left(n_{2}\right)-\mu_{X}\left(n_{2}\right)\right]\right\} \\ &=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N}\left[x\left(n_{1}, i\right)-\mu_{X}\left(n_{1}\right)\right] \cdot\left[x\left(n_{2}, i\right)-\mu_{X}\left(n_{2}\right)\right] \end{aligned}$

注：以上所有的统计后的量都是关于 $n$ 的变量

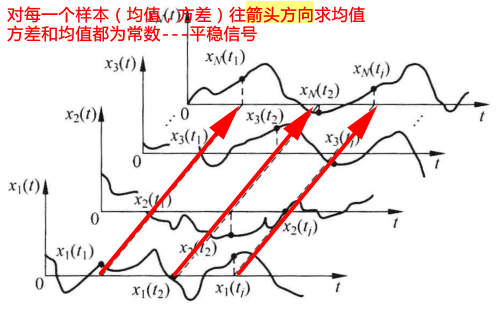
平稳随机信号描述

宽平稳（wide-sense stationary，WSS）信号，又称广义平稳信号的定义：

均值为常数

$\mu_X(n)=E\{X(n)\} = \mu_X$
方差也为常数

$\sigma^2_X(n) = E\{|X(n)-\mu_X|^2\} = \sigma^2_X$
自相关函数仅与选取点有关

$r_X(n_1,n_2) = E\{X*(n)X(n+m)\}=r_X(n_2-n_1)$

再看随机信号图：

例12.2.1 随机相位正弦序列

$X(n) = A sin (2\pi fn T_s+\Phi)$

式中 $A,f$ 均为常数， $\Phi$ 是一随机变量，在 $0\sim 2\pi$ 内服从均匀分布，即根据不同的 $\Phi_1,\Phi_2,\dots,\Phi_k$ 生成不同的 $x_1(n),x_2(n),\dots,x_k(n)$ 信号，其中每一个 $x_1(n)$ 是一串离散时间序列。

$p(\varphi)=\left\{\begin{array}{ll} \frac{1}{2 \pi} & 0 \leqslant \varphi \leqslant 2 \pi \\ 0 & other \end{array}\right.$

解答：

均值为：

$\mu_X(n) = E\{Asin(2\pi fnT_s+\Phi)\} = \int_0^{2\pi}Asin(2\pi fT_sn+\phi)\frac{1}{2\pi}d\phi=0$
自相关函数为：

$\begin{aligned} r_{X}\left(n_{1}, n_{2}\right) &=E\left\{A^{2} \sin \left(2 \pi f n_{1} T_{s}+\Phi\right) \sin \left(2 \pi f n_{2} T_{s}+\Phi\right)\right\} \\ &=\frac{A^{2}}{2 \pi} \int_{0}^{2 \pi} \sin \left(2 \pi f n_{1} T,+\varphi\right) \sin \left(2 \pi f n_{2} T_{s}+\varphi\right) \mathrm{d} \varphi \\ &=\frac{A^{2}}{2} \cos \left[2 \pi f\left(n_{2}-n_{1}\right) T_{s}\right] \end{aligned}$

所以随机相位正弦波是宽平稳的。

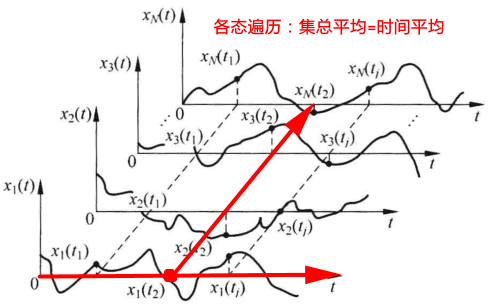
平稳随机信号的各态遍历性

上面已经介绍了随机信号 $X(n)$ 的均值、方差、均方及自相关函数等，均是建立在随机变量 $x_i(n)$ 集总平均的意义上的，如求解自相关函数：

$r_{x}(m)=E\{X(n) X(n+m)\}=\lim _{N \rightarrow \infty} \frac{1}{N} \sum_{i=1}^{N} x(n, i) x(n+m, i)$

但是要精确地求出上值，需要无穷多个样本，这在实际工作中是不可能的。

上图中，若我们要精确地求出红点的值，就要沿样本方向求均值，但是这做不到。但是假定单一样本函数随时间的变化的过程可以包含该信号所有样本函数的取值经历。这句话的含义是沿着时间 $t$ ，每个时间节点 $t$ 都可以看做独立测试的一个样本 $i$ （集总平均=时间平均）。故上述的自相关函数可以改写为：

$r_X(m)=\lim_{M\rightarrow \infin}\frac{1}{2M+1}\sum_{n=-M}^Mx(n)x(n+m)$

判断例12.2.1 中的正弦序列信号是否为平稳随机信号

集总平均：

$\begin{aligned} \mu_X(n) =& 0 \\ r_X(n_1,n_2)= &\frac{A^2}{2}cos(2\pi f m T_s) \end{aligned}$
时间平均

$\begin{aligned} \mu_{x}= &\lim _{M \rightarrow \infty} \frac{1}{2 M+1} \sum_{n=-M}^{M} A \sin \left(2 \pi f n T_{s}+\varphi\right)=0=\mu_{X}\\ r_{x}(m)=&\lim _{M \rightarrow \infty} \frac{1}{2 M+1} \sum_{n=-M}^{M} A^{2} \sin \left(2 \pi f n T_{s}+\varphi\right) \sin \left[2 \pi f(n+m) T_{s}+\varphi\right] \\ = &\frac{A^2}{2}cos(2\pi f m T_s) \end{aligned}$

可以发现时间平均=集总平均，是平稳随机信号。

平稳随机信号的功率谱

根据Wiener-Khintchine定理，自相关函数和平稳随机信号的功率谱互为傅里叶变换：

功率谱的计算

$\begin{aligned} P_{X}\left(\mathrm{e}^{\mathrm{i} \omega}\right) &=\sum_{m=-\infty}^{\infty} r_{X}(m) \mathrm{e}^{-\mathrm{j} \omega m} \\ P_{X Y}\left(\mathrm{e}^{\mathrm{i} \omega}\right) &=\sum_{m=-\infty}^{\infty} r_{X Y}(m) \mathrm{e}^{-\mathrm{j} \omega m} \end{aligned}$

自相关函数的计算
$r_X(m)=\frac{1}{2\pi}\int_{-\pi}^{\pi}P_X(e^{j\omega m})e^{j\omega m }d\omega$
其中 $m=0$ 时，反映了信号的平均功率
$r_X(0) = \frac{1}{2\pi}\int_{-\pi}^{\pi}P_X(e^{j\omega m})d\omega = E\{|X(n)|^2\}$

例题：平稳信号 $X(n)$ 的自相关函数 $r_X(m)=a^{|m|}$ ， $|a|<1$ ，求其功率谱。

$\begin{aligned} P_{X}\left(\mathrm{e}^{\mathrm{i} \omega}\right)=&\sum_{m=-\infty}^{\infty} a^{|m|} \mathrm{e}^{-\mathrm{i} \omega m}=\sum_{m=0}^{\infty} a^{m} \mathrm{e}^{-\mathrm{j} \omega m}+\sum_{m=-\infty}^{0} a^{-m} \mathrm{e}^{-\mathrm{i} \omega m}-1 \\ = &\frac{1}{1-a \mathrm{e}^{-\mathrm{i} \omega}}+\frac{1}{1-a \mathrm{e}^{\mathrm{i} \omega}}-1=\frac{1-a^{2}}{1+a^{2}-2 a \cos \omega}, \quad|a|<1 \end{aligned}$

实际功率谱

实际工程中所遇到的功率谱可分为三种：

平的谱：白噪声谱
线谱：正弦信号所组成的功率谱
ARMA谱：既有峰点又有谷点