文章
68
标签
25
分类
55
首页
归档
标签
分类
链接
About
SklearnAPI
列表
目录
  1. 前言
  2. 牛顿法
    1. 牛顿法求根
    2. 牛顿法求驻点
      1. 当n=1时
      2. 当n>1时：牛顿-拉夫森迭代法（Newton-Raphson method）
    3. 算法流程
  3. 阻尼牛顿法
  4. 算法总结与分析
  5. 其余内容（非重点）
    1. 拟牛顿法
    2. 牛顿法计算平方根
  6. 参考资料：
牛顿法
字数总计: 2.5k|阅读时长: 11 分钟|阅读量:

前言

机器学习算法中经常需要求解凸函数的极值求解问题，一般来说解析解是很难求得的，或者即使有解析解，出于某种原因（比如计算量过大，矩阵求逆等）也不会使用解析解。之前学习skleran库时LogisticRegression函数中有个solver参数，可以设置逻辑回归损失函数的优化方法，又牵涉到这部分的内容，所以这里做个总结

参数 说明
lbfgs 拟牛顿法
newton-cg 牛顿法家族的一种
sag 随机平均梯度下降

牛顿法

牛顿法求根

使用函数的泰勒级数前面几项来找方程 f(x)=0f(x)=0的根。
注：x=[x1,x2,…,xn]x=[x_1,x_2,\dots,x_n]是n维空间向量。将函数在其根的附近进行泰勒展开：

f(x)=f(x0)+f′(x0)(x−x0)+12f′′(x0)(x−x0)2+Rn(x)f(x) = f(x_0)+f'(x_0)(x-x_0)+\frac{1}{2}f''(x_0)(x-x_0)^2+R_n(x)

设x=xtx=x_t时，是函数f(x)f(x)的根，即f(xt)=0f(x_t)=0，若设xkx_k为xtx_t的估计值。首先我们在x=xkx=x_k处进行泰勒一阶展开，得：

f(x)=f(xk)+f′(xk)(x−xk)+Rn(x)≈0+f′(xk)(x−xk)\begin{aligned} f(x) &=f\left(x_{k}\right)+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right)+R_{n}(x) \\ & \approx 0+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right) \end{aligned}

根的迭代方式为：

x=xk+f(x)f′(x)x = x_k + \frac{f(x)}{f'(x)}

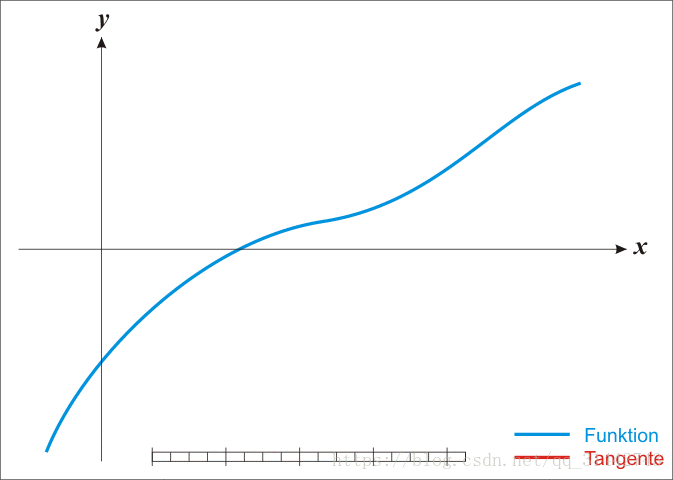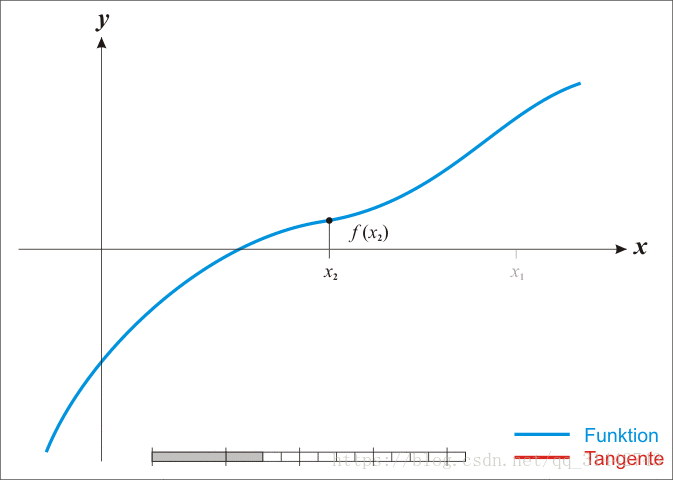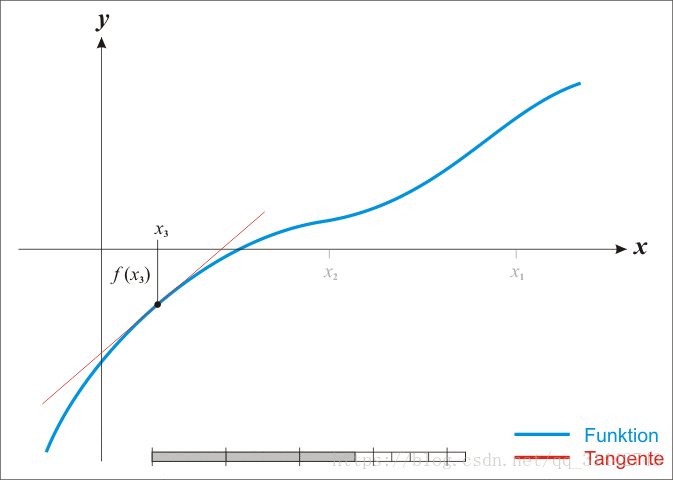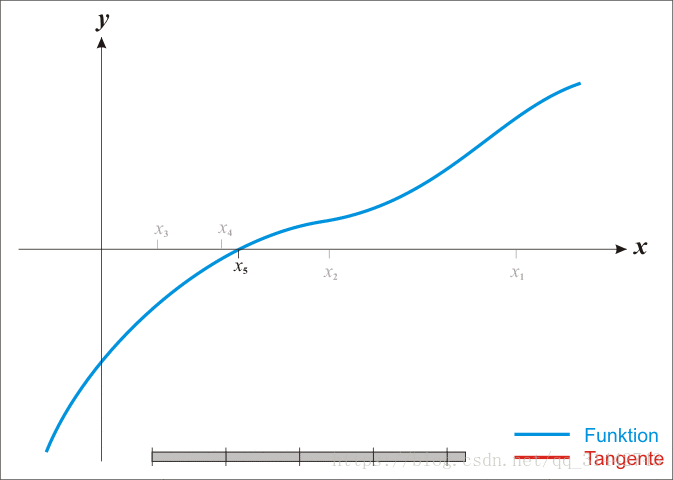
迭代过程图，见下：

观察根的迭代方式，此方法也被称作为切线法。

牛顿法求驻点

其需要解决的问题可以描述为：对于目标函数f(x)，在无约束条件的情况下求它的最小值。

min⁡x∈Rnf(x)\min_{x\in R^n}f(x)

牛顿法求驻点，需要用到二阶导函数，从简单的开始分析，设置n为x的维度。

当n=1时

设x=xtx=x_t时，函数f(x)f(x)取得最小值，目标希望求得xtx_t，若设xkx_k为xtx_t的估计值。首先我们在x=xkx=x_k处进行泰勒二阶展开，得：

f(x)=f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2+Rn(x)≈f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2\begin{aligned} f(x) &=f\left(x_{k}\right)+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{k}\right)\left(x-x_{k}\right)^{2}+R_{n}(x) \\ & \approx f\left(x_{k}\right)+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{k}\right)\left(x-x_{k}\right)^{2} \end{aligned}

对f(x)f(x)求导，得：

f′(x)=f′(xk)+f′′(xk))(x−xk)f'(x) = f'(x_k)+f''(x_k))(x-x_k)

令f′(x)=0f'(x)=0，得：

x=xk−f′(xk)f′′(xk)x = x_k - \frac{f'(x_k)}{f''(x_k)}

当n>1时：牛顿-拉夫森迭代法（Newton-Raphson method）

当xx为高维向量时，对f(x)f(x)对xx的一阶导数是一个向量，对xx的二阶导数为N∗NN*N的矩阵【海塞矩阵】。

f′(x)=(∂f(x)∂x1,∂f(x)∂x2,…,∂f(x)∂xn)f′′(x)=[∂2f(x)∂xi∂xj]n×n=[∂2f∂x12∂2f∂x1∂x2⋯∂2f∂x1∂xn∂2f∂x2∂x1∂2f∂x22⋯∂2f∂x2∂xn⋮⋮⋱⋮∂2f∂xn∂x1∂2f∂xn∂x2⋯∂2f∂xn2]\begin{aligned} f'(x)=&(\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2},\dots,\frac{\partial f(x)}{\partial x_n}) \\ f''(x) =& \left[ \frac{\partial^2f(x)}{\partial x_i\partial x_j} \right]_{n\times n} \\ = &\left[\begin{array}{cccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \frac{\partial^{2} f}{\partial x_{1} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \frac{\partial^{2} f}{\partial x_{2} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{2}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{2} \partial x_{n}} \\ \vdots & \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \frac{\partial^{2} f}{\partial x_{n} \partial x_{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] \end{aligned}

为了便于表达，其中gkg_k是向量，HkH_k为海塞矩阵

则高维向量的迭代公式为：

xk+1=xk−Hk−1gkx_{k+1} = x_k - H_k^{-1}g_k

以上被称为原始的牛顿迭代法，迭代格式中的搜索方向为dk=−Hk−1⋅gkd_k=- H_k^{-1}\cdot g_k称为牛顿方向。

算法流程

设置导函数的终止阈值a，当∥f′(xk)∥<a\|f'(x_k)\|<a时，则停止计算。得到x=xkx=x_k即为所求。

  1. 给定初值x0x_0和精度阈值ϵ\epsilon，并令 k:=0k:=0
  2. 计算gkg_k和HkH_k
  3. 若 ∥gk∥<ϵ\|g_k\|<\epsilon，则停止迭代；否则确定搜索方向dk=−Hk−1⋅gkd_k=- H_k^{-1}\cdot g_k
  4. 计算新的迭代点xk+1:=xk+dkx_{k+1}:=x_k+d_k
  5. 令k:=k+1k:=k+1，循环第2步。

可以发现原始牛顿法迭代公式中没有步长因子，而是定步长迭代，对于非二次型目标函数，有时会使函数值上升，即出现f(xk+1)>f(xk)f(x_k+1)>f(x_k)的情况，这时，牛顿法不能收敛，从而导致计算失败。对于这种情况，可以使用阻尼牛顿法来解决。

阻尼牛顿法

阻尼牛顿法的思想很简单，既然传统的牛顿法迈的步子太大（定步长），那我就人为的设置一个参数去控制你这个步子，即步长因子λk\lambda_k。每次迭代方向与原始牛顿法的方向相同，但是迭代前先找到最优的步子的大小，即

λk=argmin⁡λ∈Rf(xk+λdk)\lambda_k = arg\min_{\lambda \in R}f(x_k+\lambda d_k)

算法流程相较于原始牛顿法，只需要修改第四步的迭代方式：

xk+1=xk+λkdkx_{k+1} = x_k + \lambda _kd_k

算法总结与分析

牛顿法是梯度（下降）法的进一步发展，梯度法利用目标函数的一阶偏导数信息、以负梯度方向作为搜索方向，只考虑目标函数在迭代点的局部性质；而牛顿法不仅使用目标函数的一阶偏导数，还进一步利用了目标函数的二阶偏导数，这样就考虑了梯度变化的趋势，因而能更全面地确定合适的搜索方向以加快收敛，它具二阶收敛速速度。

给出梯度下降的一阶Taylor近似：

f(x)≈f(xk)+f(xk)T(x−xk)f(x) \approx f(x_k) + f(x_k)^{T}(x-x_k)

给出二阶Taylor近似：

f(x)≈f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2f(x) \approx f\left(x_{k}\right)+f^{\prime}\left(x_{k}\right)\left(x-x_{k}\right)+\frac{1}{2} f^{\prime \prime}\left(x_{k}\right)\left(x-x_{k}\right)^{2}

对于点xkx_k，不同方法的下降方式：

{−f˙(xk)gradient descent−f¨(xk)−1f˙(xk)Newton−Raphsonλk[−f¨(xk)−1f˙(xk)]damping Newton−Raphson\begin{cases} -\dot{f}\left( x_k \right)& gradient\ descent\\ -\ddot{f}\left( x_k \right) ^{-1}\dot{f}\left( x_k \right)& Newton-Raphson\\ \lambda _k\left[ -\ddot{f}\left( x_k \right) ^{-1}\dot{f}\left( x_k \right) \right]& damping\ Newton-Raphson\\ \end{cases}

但牛顿法主要存在以下两个缺点：

  • 对目标函数有较严格的要求。函数必须具有连续的一、二阶偏导数，海森矩阵必须正定.
  • 计算相当复杂.除需计算梯度而外，还需计算二阶偏导数矩阵和它的逆矩阵.计算量、存储量均很大，且均以维数N的平方比增加，当N很大时这个问题更加突出。当Hessian矩阵不是很大时牛顿方法要优于梯度下降。

其余内容（非重点）

拟牛顿法

逆牛顿法主要解决计算条件苛刻以及计算量大等问题，当海森矩阵无法保持正定，不用二阶偏导数构造出可以近似海森矩阵或者海森矩阵的逆的正定对称矩阵。不同构造方法，产生不同过得拟牛顿法。更多资料请见参考资料【2】，内容太数学了，学了也没什么必要，等接触到再说把。

重新叙述一遍算法：

f′(x)≈f′(xk)+f′′(xk))(x−xk)f'(x) \approx f'(x_k)+f''(x_k))(x-x_k)

引入记号，gkg_k和HkH_k

gk+1−gk≈Hk+1(xk+1−xk)g_{k+1}-g_k \approx H_{k+1}(x_{k+1}-x_k)

再引入记号sks_k和yky_k

sk=xk+1−xk,yk=gk+1−gks_k = x_{k+1}-x_k , y_k = g_{k+1}- g_k

可写：

yk≈Hk+1⋅sky_k \approx H_{k+1}\cdot s_k

牛顿法计算平方根

算法：

f(x)=x2−a=0f′(x)=2xxn+1=xn−f(xn)f′(xn)=xn−xn2−a2xn=2xn2−(xn2−a)2xn=xn2+a2xnf(x) = x^2 -a = 0 \\ f'(x) = 2x \\ x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)} =x_{n}-\frac{x_{n}^{2}-a}{2 x_{n}}=\frac{2 x_{n}^{2}-\left(x_{n}^{2}-a\right)}{2 x_{n}}=\frac{x_{n}}{2}+\frac{a}{2 x_{n}}

程序语言：

xn:=xn2+a2xn=xn/2+a/2/xnx_{n}:=\frac{x_{n}}{2}+\frac{a}{2 x_{n}}=x_{n} / 2+a / 2 / x_{n}

参考资料：

  1. 牛顿法的具体推导–CSDN
  2. 牛顿法系统性介绍–CSDN
  3. 博客园–桂
  4. LogisticRegression参数详解
声纹识别 牛顿法
相关推荐
I-Vector算法与PLDA
安装sidekit教程
白化（Whitening）
繁