P-PCA
数据生成背景
根据白板推导我们已经知道,高斯混合模型有两种理解方式:几何角度**(非概率版本)和生成角度(概率版本)**。
模型的生成方式是:先选定一个高斯分布,再根据这个高斯分布的PDF生成数据点。所以高斯混合模型默认隐变量是离散的。而P-PCA隐变量是均值为0,方差为1的高斯分布。
概率版本与非概率版本的区别在于隐变量的分布
- 原先的隐变量为离散 --> 连续性(满足某个概率分布)
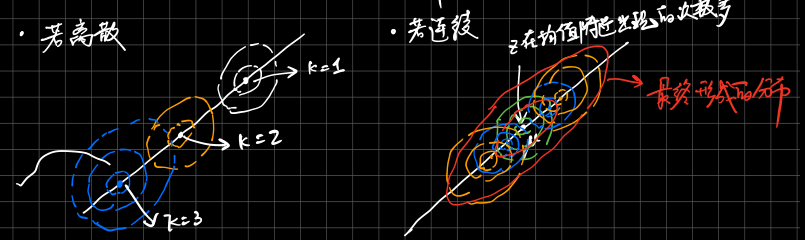
![隐变量的分布情况]()
上图中左部分是传统的GMM模型,把三个独立的高斯分布根据权重拟合成一个混合的高斯分布。而右图中有无穷多个高斯分布,若选择z均值附近被选中的概率非常高,所以拟合出的分布这里会非常高。
算法理论部分
已知: p(x) p(x∣z) p(z)
-
隐变量服从零均值单位协方差p(z)∼N(z∣0,I)
-
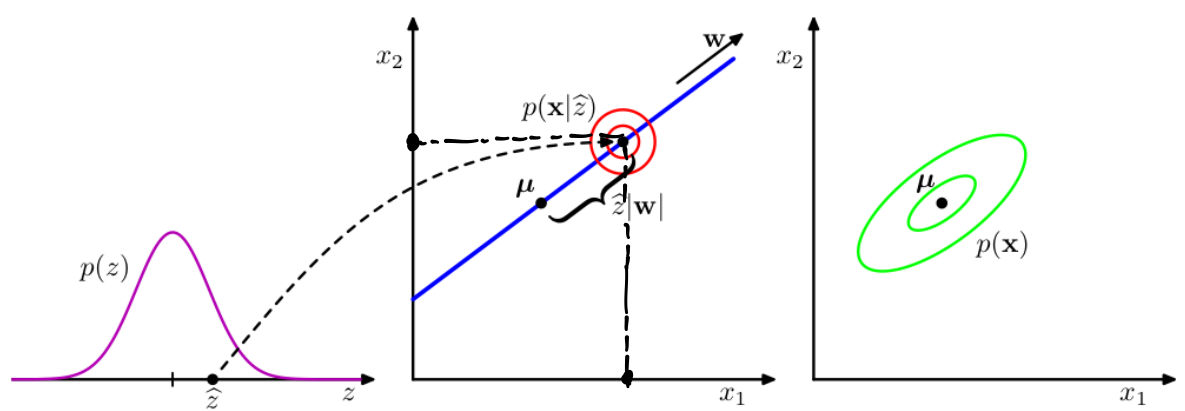
观测变量x的生成方式:x=Wz+μ+ε
![数据生成方式]()
-
p(x∣z)∼N(Wz+μ,σ2⋅I)
-
p(x)也是高斯分布,原因在于:p(x)=∫zp(x∣z)p(z)dz
推导x的PDF:
x∼N(x∣μ,WWT+σ2I)
分析:
E[x]=cov[x]=====E[Wz+μ+ε]=μE[(x−E[x])(x−E[x])T]E[(Wz+ε)(Wz+ε)T]E[WzzTWT+εzTWT+WzεT+εεT]WIWT⋅D(z)+D(ε)WWT+σ2I
其中:z 和 ε 是独立的。E(z⋅εT)=E(z)E(ε)=0
也可以直接利用方差的性质:
Var[x]===Var[Wz+μ+ε]Var[Wz]+Var[ε]W⋅I⋅WT+σ2I
对于求解p(z∣x)比较难:
首先联合概率分布的PDF:
性质:
xb⋅a=μb⋅a=Σbb⋅a=xb⋅a∼xb−ΣbaΣaa−1xaμb−ΣbaΣaa−1μaΣbb−ΣbaΣaa−1ΣabN(μb⋅a,Σbb⋅a)
又:xb=xb⋅a+ΣbaΣaa−1xa
E[xb∣xa]===Var[xb∣xa]=E[xb⋅a]+ΣbaΣaa−1xaμba+ΣbaΣaa−1xaμb+ΣbaΣaa−1(xa−μa)Var[xb⋅a]+0=Σbb⋅a
上面介绍完性质:直接套用
(xz)∼N([μ0][WWT+σ2IWWI])
其中:
cov(x,z)====E[(x−μ)(z−0)T]E[(Wz+ε)zT]E[WzzT]+E[ε⋅zT]W⋅I=W
白板书推导:
p(z∣x)∼N(WT(WWT+σ2I)−1(x−μ),I−WT(WWT+σ2I)−1W)
PRML:
M=WTW+σ2I
P(z∣x)∼N(z∣M−1WT(x−μ),σ2M−1)
根据矩阵的求逆公式:
(P−1+BTR−1B)−1BTR−1=PBT(BPBT+R)−1
可以证明上面白板书推导出的公式和PRML给出的公式是等价的。
EM算法
其中需要估计的参数是:W,μ,σ2
Likelihood
lnp(X∣W,μ,σ2)===n=1∑Nlnp(xn∣W,μ,σ2)−2NDln(2π)−2Nln∣Σ∣−21n=1∑N(xn−μ)TΣ−1(xn−μ)−2N{Dln(2π)+ln∣Σ∣+Tr(Σ−1S}
常规:MLE求极值能得到近似封闭解
Joint Likelihood
lnp(X,Z∣W,μ,σ2)=E[lnp(x,z∣W,μ,σ2)]=n=1∑N{lnp(xn∣zn)+lnp(zn)}−n=1∑N{2Dln(2πσ2)+21Tr(E[znznT])+2σ21∥xn−μ∥2−σ21E[zn]TWT(xn−μ)+2σ21Tr(E[znZnT]WTW)+2Mln(2π)}
其中,涉及需要估计充分统计量,需要依赖后验概率
E步:
Ez∣x[zn]=Ez∣x[znznT]==M−1WT(xn−xˉ)cov[zn]+E[zn]E[zn]Tσ2M−1+E[zn]E[zn]T
M步:固定后验概率,即充分统计量固定(看作常数)
首先明确更新的变量为:σ2和W
举例说明:∂W∂Δ
Δ=−n=1∑N{−σ21E[zn]TWT(xn−μ)+2σ21Tr(E[znznT]WTW)}
为了方便求导,利用迹的性质:
Tr(ABC)=Tr(BCA)=Tr(CAB)
故上面公式中:
Tr(E[znznT]WTW)=Tr(WTWE[znznT])
拉格朗日求导:
∂W∂Δ=n=1∑N{−σ21E[zn]T(xn−μ)+2σ212WE[znznT]}=0
可以推出:
Wnew=[n=1∑NE[zn]T(xn−μ)][n=1∑NE[znznT]]−1
同理可得:(这里具体推导省略)
σ^new=ND1n=1∑N{∥xn−xˉ∥−2E[zn]TWnewT(xn−xˉ)+Tr(E[znznT]WnewTWnew)}
![数据生成方式]()