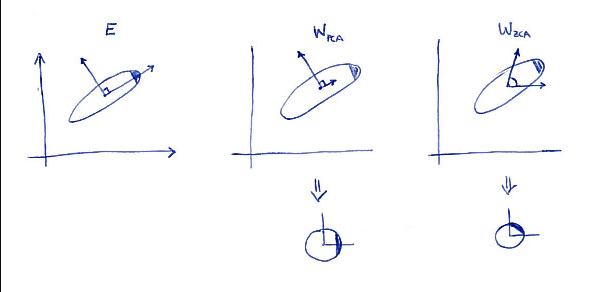
白化(Whitening)
白化的结果
- 使数据的不同维度去相关;(对角协方差矩阵)
- 使数据的每个维度的方差为1;(协方差矩阵是单位矩阵I)
为什么使用白化?
假设训练数据是图像,由于图像中相邻像素之间具有很强的相关性,所以用于训练时输入是冗余的。白化的目的就是降低输入的冗余性。
比如在独立成分分析(ICA)中,对数据做白化预处理可以去除各观测信号之间的相关性,从而简化了后续独立分量的提取过程,而且,通常情况下,数据进行白化处理与不对数据进行白化处理相比,算法的收敛性较好。
两种白化方式
PCA 白化
其实我们之前学的PCA算法中,可能PCA给我们的印象是一般用于降维操作。然而其实PCA如果不降维,而是仅仅使用PCA求出特征向量,然后把数据X映射到新的特征空间,这样的一个映射过程,其实就是满足了我们白化的第一个性质:除去特征之间的相关性
PCA白化算法的实现过程:
- PCA操作,求出新特征空间中X的新坐标。
- 在新坐标系下进行方差归一化操作
ZCA 白化
ZCA白虎是在PCA白化的基础上,又进行处理的一个操作。具体的实现是把上面PCA白化的结果,又变换到原来坐标系下的坐标:
ZCA中Z代表 zero - phase 零相位,说明此数据与原数据没有发生旋转
ZCA白化算法的实现过程:
- PCA操作,求出新特征空间中X的新坐标。
- 在新坐标系下进行方差归一化操作
- 再投影回原坐标系
图解PCA
二维均匀分布:rand
![]() 二维高维分布:
二维高维分布:randn
![]()
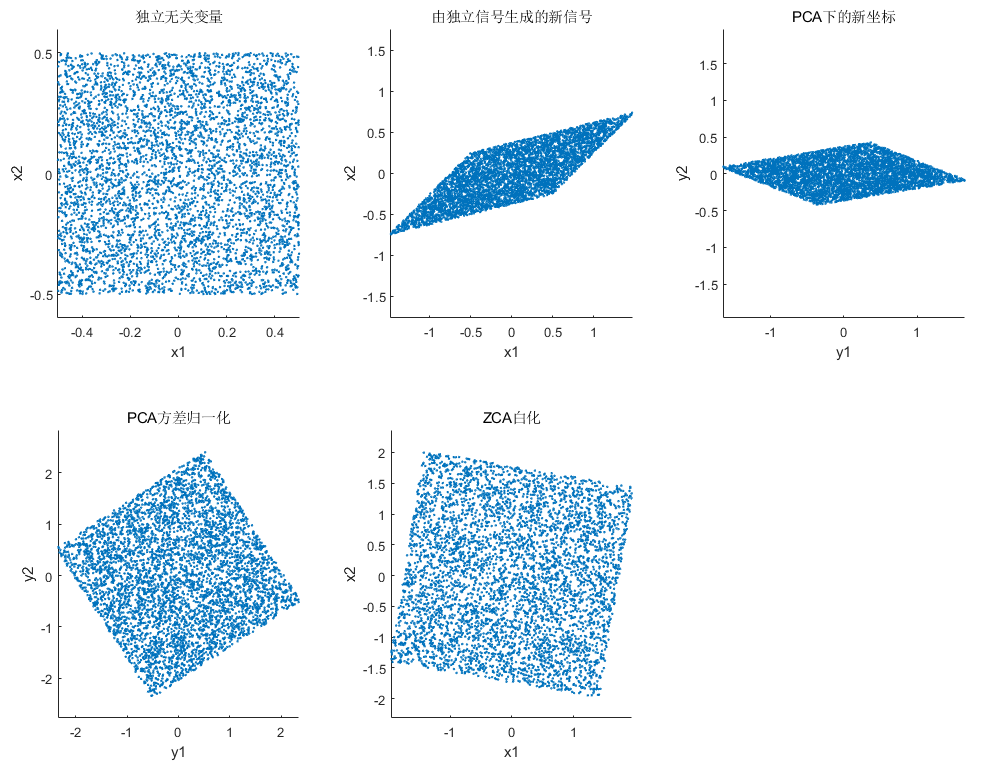
注:这里的 PCA 白化和 ZCA 白化看上去一样其实是不一样的,PCA 的数据在维度方向是无关的,相当于原数据发生了一个旋转,ZCA 则与原数据没有发生旋转,从第一个图可以发现这种旋转方式。下图可以反映这种变换。
![]()
代码部分:
close all
[s1, s2] = RandStream.create('mrg32k3a', 'NumStreams', 2);
x1 = randn(5000,1)-0.5;
x2 = randn(5000,1)-0.5;
figure();
set(gcf,'color','w')
subplot(2,3,1)
scatter(x1,x2,2)
axis equal
xlabel("x1")
ylabel("x2")
title("独立无关变量")
y1 = x1 + 2*x2;
y2 = 1*x1 + 0.5*x2;
subplot(2,3,2)
scatter(y1,y2,2)
axis equal
xlabel("x1")
ylabel("x2")
title("由独立信号生成的新信号")
X = [y1 y2];
X = X - mean(X,1);
[U, D, V] = svd(1/4999*X'*X);
X_PCA = X*U ;
subplot(2,3,3);
scatter(X_PCA(:,1),X_PCA(:,2),2)
axis equal
xlabel("y1")
ylabel("y2")
title("PCA下的新坐标")
X_PCA_std = X_PCA ./ sqrt(diag(D))';
subplot(2,3,4);
scatter(X_PCA_std(:,1),X_PCA_std(:,2),2)
axis equal
xlabel("y1")
ylabel("y2")
title("PCA方差归一化")
cov(X_PCA_std(:,1))
cov(X_PCA_std(:,2))
subplot(2,3,5);
X_ZCA = U*X_PCA_std';
scatter(X_ZCA(1,:),X_ZCA(2,:),2)
axis equal
xlabel("x1")
ylabel("x2")
title("ZCA白化")
|
数学原理
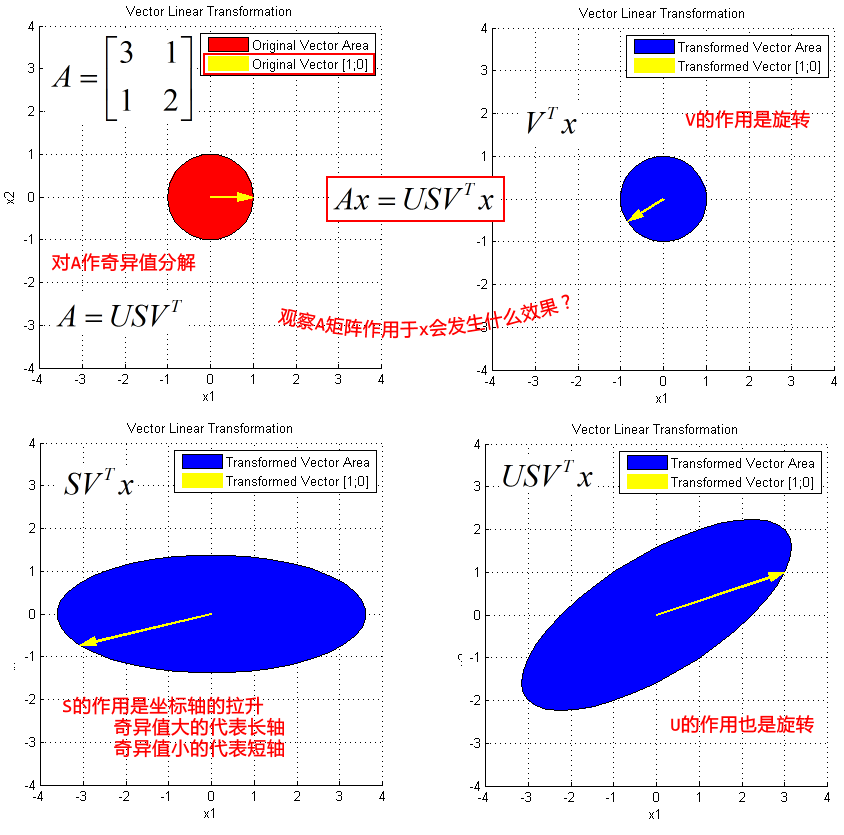
SVD图解⭐️
图解奇异值分解:https://my.oschina.net/findbill/blog/535044
![]()
数学算法
摘自:https://www.cnblogs.com/demian/p/7627324.html
算法流程:
给定训练数据集(假设每个特征都具有零均值):X∈Rn×m,n 是数据维度;m 是样本个数。
-
计算数据的协方差矩阵为:
注:svd中输入的必须是协方差,即必须要有分母,这样算出来的奇异值矩阵S,才可以用作PCA的方差归一化处理
Σ=m−11XXT
- 对协方差矩阵做奇异值分解:
[U,S,V]=svd(Σ)
-
PCA + 特征方差归一化处理:
XPCAWhite=S−21UTX=⎣⎡λ11000⋱000λn1⎦⎤Xrotate
其中,Xrotate 就是原数据在主成分轴上的投影,而 S−21 相当于对每一个主轴上的数据做一个缩放,缩放因子就是除以对应特征值的平方根。以下两个公式等价:
方差归一化:
XPCAwhite=std(Xrotate)Xrotate
利用奇异值放缩达到归一化的目的:
XPCAwhite=λi+εXrotate
-
ZCA 白化:PCA 白化后的数据重新变换回原来的空间
XZCAwhite=UXPCAwhite
考察白化的合法化:
PCA白化的结果就是:对角协方差为I
PCAWhite∑=m1XPCAwhiteXPCAwhile=S−21UT(m1XXT)U(S−21)T=S−21UT∑US−21=S−21(UTU)S(UTU)S−21=S−21ISIS−21=I
XZCAwhite=UXPCAwhite
ZCA 白化也是一个合法的白化。
ZCAwhite∑=m1XZCAwhiteXZCAwhite=Um1XZCAwhiteXZCAwhiteUT=UIUT=I
正则化:
实践中需要实现PCA白化或ZCA白化时,有时一些特征值λi在数值上接近于0,这样在缩放步骤时我们除以 λi 将导致除以一个接近0的值;这可能会导致数据上溢(赋为最大值)或造成数值不稳定。因而在实践中,我们使用少量的正则化实现这个缩放过程,即在取平方根和倒数之前给特征值加上一个很小的常数ε:
S21=⎣⎡λ1+ε1000⋱000λn+ε1⎦⎤
一般取值为 ε≈10−5。
![]() 二维高维分布:
二维高维分布: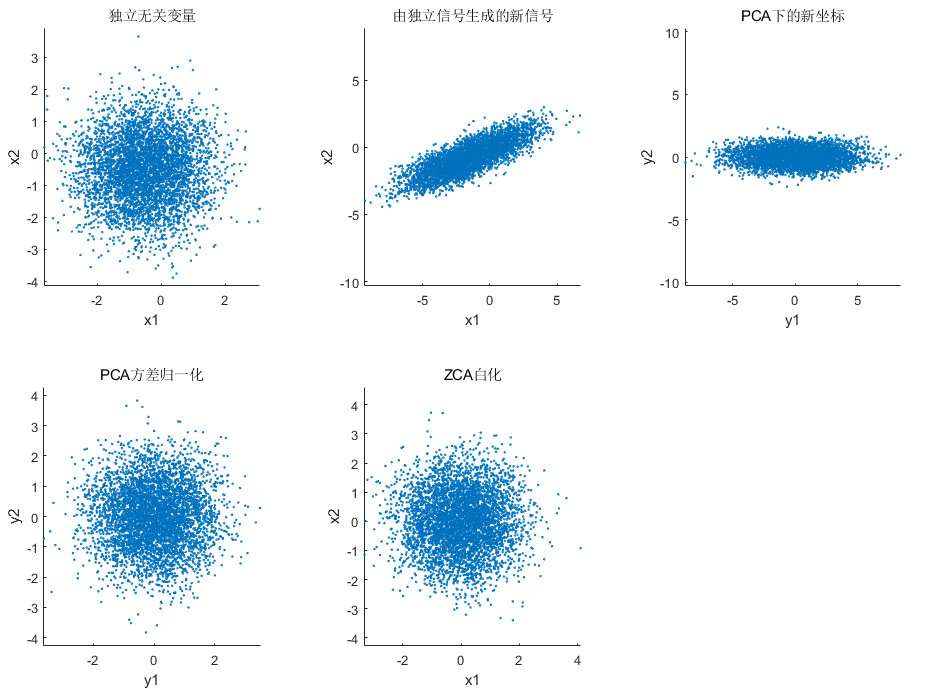

 二维高维分布:
二维高维分布: