Matlab官方文档–分类Demo
Fisher’s Iris Data
Fisher的iris data 的特征包含如下:
- Sepal length in cm
- Sepal width in cm
- Petal length in cm
- Petal width in cm
load fisheriris |
Linear and Quadratic Discriminant Analysis
fitcdiscr可以调用不同的discriminant analysis方法。默认使用LDA取分类数据。
lda = fitcdiscr(meas(:,1:2),species); # 默认LDA训练 |
计算重构错误,也即错分误差(再训练样本中错分的比例)
ldaResubErr = resubLoss(lda) |
也可以计算混淆矩阵,i代表原先的类别,j代表预测的类别。
[ldaResubCM,grpOrder] = confusionmat(species,ldaClass) |
绘制分类错误的点,strcmp字符比较函数
bad = ~strcmp(ldaClass,species); |
绘制判别边界,待预测空间内打点 --》 预测
[x,y] = meshgrid(4:.1:8,2:.1:4.5); |
对于某些问题来说,LDA不够用了,需要用到quadratic discriminant analysis (QDA)
qda = fitcdiscr(meas(:,1:2),species,'DiscrimType','quadratic'); |
你可以计算resubstitution error(重构误差),通常会低估了test error。我们会用交叉验证,比如10 - 折。随机划分数据集。1折验证,9折计算。为了保证每次随机性的结果,所以需要设置随机种子。
rng(0,'twister'); |
首先使用cvpartition取划分出10个不同的子数据
cp = cvpartition(species,'KFold',10) |
crossval 和 kfoldLoss 能计算LDA 和QDA的错分误差
cvlda = crossval(lda,'CVPartition',cp); |
Naive Bayes Classifiers
上面的fitcdiscr只能提供两种模式 ‘DiagLinear’ and ‘DiagQuadratic’。它们相似于 ‘linear’ and ‘quadratic’,但是是对角协方差估计,可以看作是Naive Bayes Classifier的特殊形式。因为NBC 可以根据标签有条件的设置变量间的独立。尽管变量间的class-conditional independence通常是不对的,但是实际例子效果不错。
fitcnb可以被使用过去创建一个更加通用的naive Bayes classifier的类型。
通常默认每个类是服从高斯分布,你可以计算resubstitution error 和 cross-validation error。
nbGau = fitcnb(meas(:,1:2), species); |
迄今为止你已经假设了每个类别中的变量服从多元高斯分布。通常是合理的假设,但是有的时候你不是很希望取做出这个假设,或者你已经很明显的可以看出这个是不合理的。现在尝试给每个类别中的变量建模通过使用一个kernel density estimation,这是一个更加灵活的非参数化技术。这里我们设置 kernel 给 box 。
nbKD = fitcnb(meas(:,1:2), species, 'DistributionNames','kernel','Kernel','box'); |
Decision Tree
t = fitctree(meas(:,1:2), species,'PredictorNames',{'SL' 'SW' }); |
另一种方式取可实话决策树:
view(t,'Mode','graph'); |
查看误差:
dtResubErr = resubLoss(t) |
可以通过上面的结果可以发现 重构误差要远远小于cross error,原因可以通过绘制两个误差曲线的变化曲线解释:
若需要捕获决策树每层的误差,需要加上’Subtrees’,‘all’
resubcost = resubLoss(t,'Subtrees','all'); |
可以发现这里需要选择 cross - validation error 作为默认的误差方法,以此选择决策树的层数。可以通过以下的命令来直接删减树枝。
pt = prune(t,'Level',bestlevel); |
查看误差:
cost(bestlevel+1) |
SOM
这里简单的介绍SOM的Matlab的过程。
1.导入数据
首先导入数据,因为每个人的数据是不同的,特别说明SOM属于无监督学习,所以只需要准备训练数据即可,无需标签数据。这里注意的维度是
load fisheriris |
2.创建Neural Network
通过selforgmap可以简单搭建一个SOM的专用网络模型。因为SOM属于一个特殊的神经网络模型,单输入单输出,且隐藏网络具有拓扑结构,无需输出结果。
selforgmap函数的记忆方法是英文Self - organization-map的缩写。
net = selforgmap([8,8]) |
我一开始不小心把这个窗口关了,不知道怎么再打开,只需要view以下网络,这个窗口又打开了。
上面发现input的输入是0,因为这个时候还没有输入数据进去。
[net,tr] = train(net,x); |
这里有个命令可以打开图形化界面,在这个界面提供一些可以很方便地帮助我们快速的可视化聚类的结果。
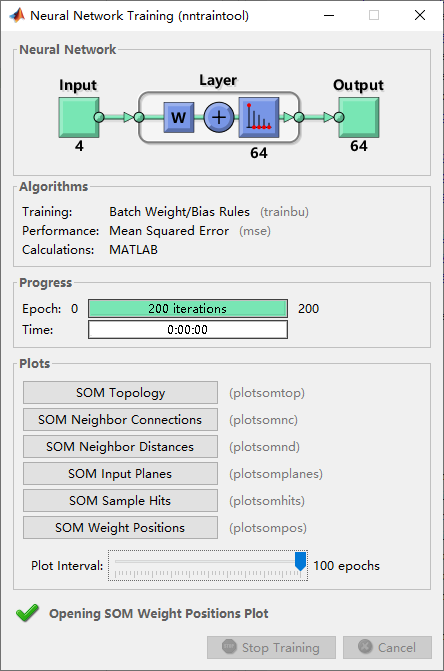
2.1 神经网络中的细节设置
在命令窗下输入net可以查看训练过程中的一些属性参数:net
# functions: |
参考输入:
net.trainParam.showWindow = true # 布尔值,训练时是否打开GUI界面 |
参考答应输出:
>> [net,tr] = train(net,x); |
3.预测聚类结果
做到上面这一步,整个聚类过程其实就已经完成了,因为SOM属于无监督聚类,所以只需要训练数据即可,若是需要用训练好的网络对类别进行预测,直接调用net方法。
我一般习惯会先习惯查看一下Weight Positions值,因为权重相当于一个小中心点,大致可以看出聚类的效果如何。但是对于高维数据,通过可视化方法查看聚类效果就比较差了,并且为了后续的分析处理,这里将数据集150个样本点 到隐藏层的 64 个神经元上。【其实这个过程就是机器学习中的predict,matlab里面称为evaluate】
y = net(x); # 直接可以evaluate 出 output,默认输出混淆矩阵 |
还可以通过在命令窗下输入net查看其余的method方法。
# methods: |
4.可视化结果
可以画出SOM的Topology图
plotsomtop(net) |
还可以画出每个神经元上赢得的样本个数
plotsomhits(net,x) |
上面这张图反映了样本对初始六角网格的影响,但是最终的结果还是网格和特征之间的连接权重决定的。
plotsomplanes(net) |
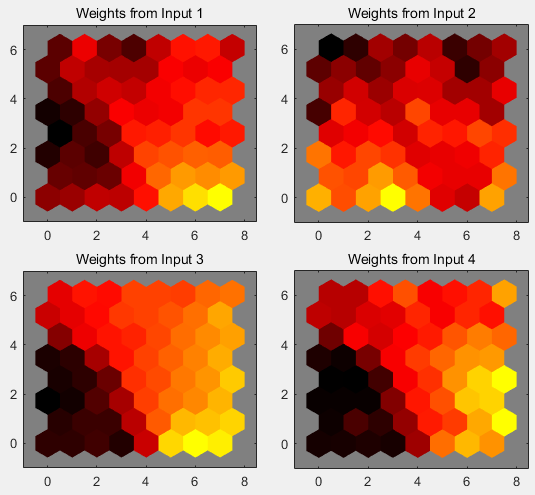
颜色越深说明权重越大,因为SOM中权重和input基本上可以看作是一个东西,因为计算的就是dist距离最小的那个值作为激活权重。比如 weights 1图中的颜色越重,说明聚类中心在x1这个维度中的值越大。
代码总结:
| 函数 | 作用 |
|---|---|