黑马程序员–聚类

通过对无标记训练样本的学习找到数据的内在性质与规律。

算法效果衡量标准

1. SSE ：误差平方和

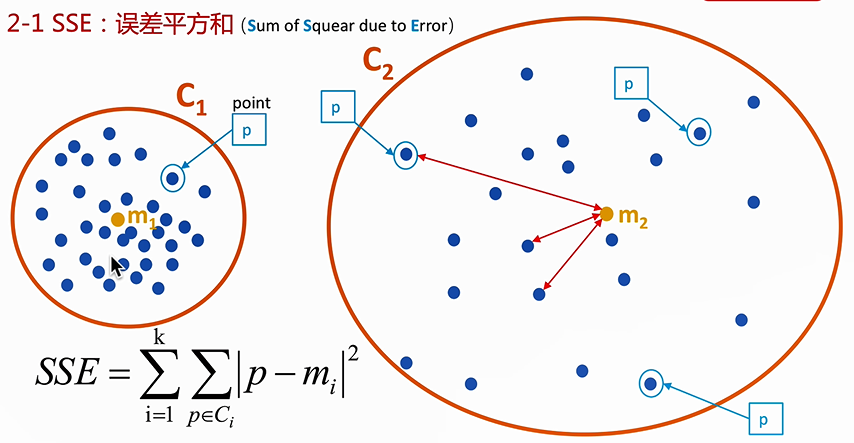
先求一个圈内的对于中心点的平方和，再将所有圈的平方和加起来就是SSE指标

迭代效果动图对比

横轴是迭代的次数，纵轴是SSE指标，SSE指标总体上反映的是聚类的离散程度。下面反映的是对**初始中心(质心)**的影响。

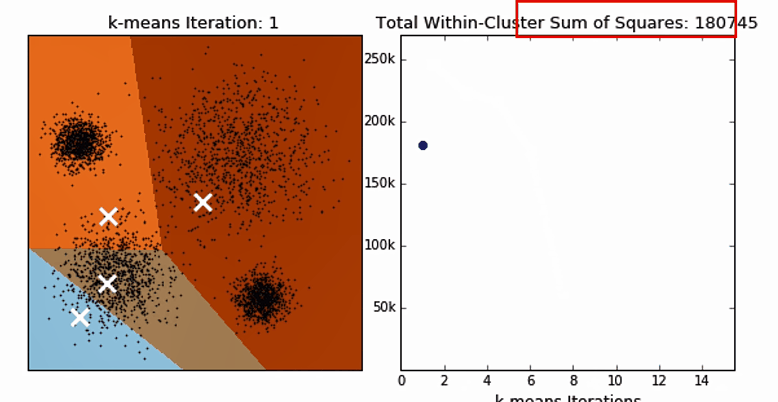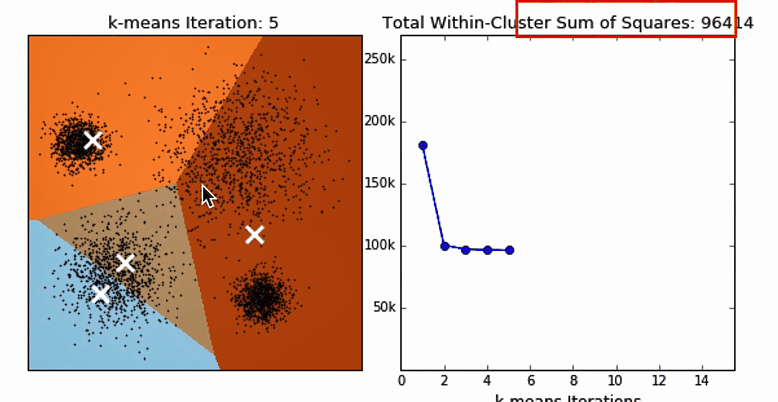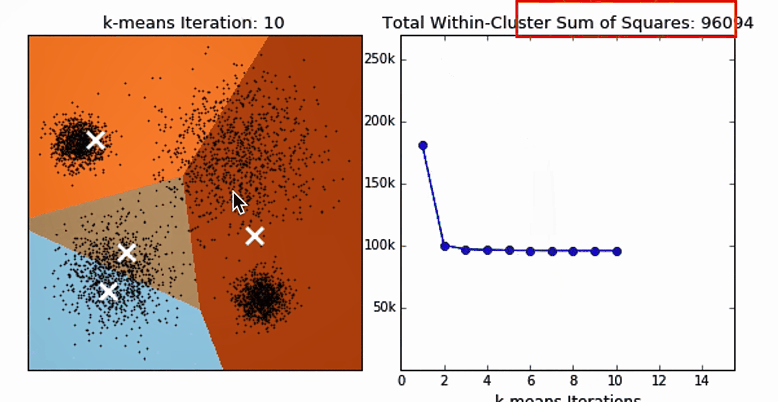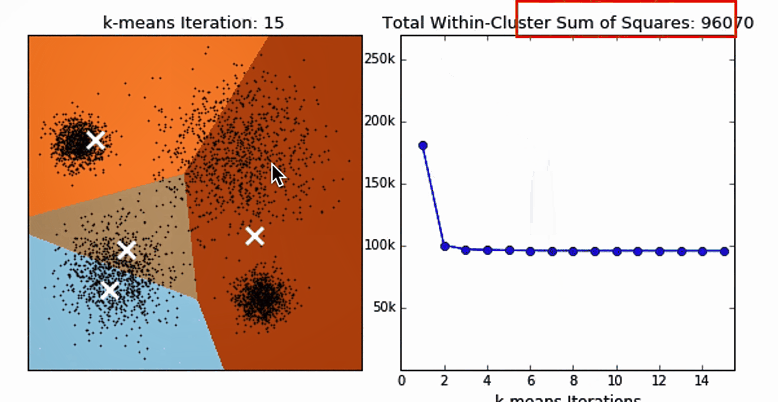
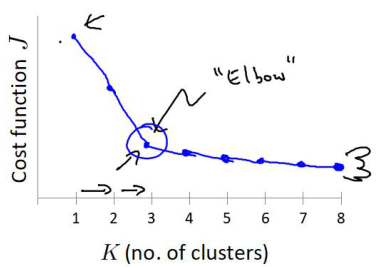
超参数K值的确定–肘部法

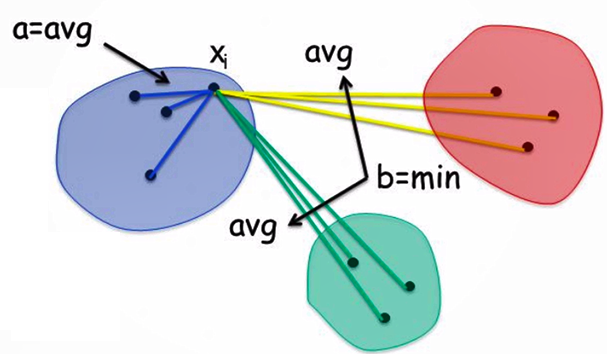
2. 轮廓系数

$S(i)= \frac{b(i)-a(i)}{max\{a(i),b(i)\}}$

$b(i)$ 指的是某点到其他聚类的最小的距离平均值
$a(i) $指的是某点到自己类内的距离平均值
S(i) 的范围为[-1,1]
每次聚类后，每个样本都会得到一个轮廓系数，当它为1时，说明这个点与周围簇距离较远，结果非常好；当它为0，说明这个点可能处在两个簇的边界上，当值为负时，暗含该点可能被误分了。

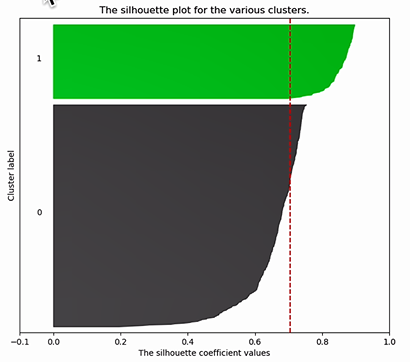
对于以下应该聚2类好，还是4类好？

2类，样本数不均衡（轮廓系数=0.70）	4类样本数均衡（轮廓系数=0.65）

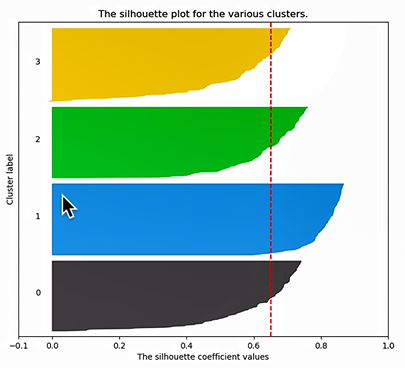轮廓系数并非越高越好，还需要考虑样本的均衡做出选择。

3. Calinski-Harabasz Index(CH系数)

核心：用尽量少的类别聚出更多的样本。所以指标中有与样本数量有关的指标m

$CH(k)=\frac{SSB}{SSW}\frac{m-k}{k-1}$

其中：

$SSW = \sum_{i=1}^m\|x_i-C_{pi}\|^2$

$SSB = \sum_{i=1}^k n_j\|C_j-\bar{X}\|^2$

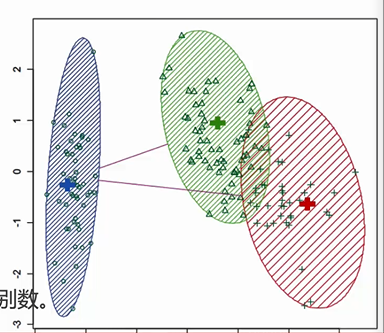
这里解释以下为啥SSB前面会乘上一个系数，因为SSB计算的是类间权重，因为不同的类的样本个数不一样，如下图，先计算每类中心与总体均值（在下图的空白处）的差值的平方，再按照权重累加所有的差值。

指标解读：

$m-k$ 的含义是：反映的是降维的强度，如从100个样本聚3类就比从4个样本聚3类的效果强。
除以 $k-1$ 的含义是：k值越到，说明聚的越细，如100个样本聚99类则失去意义。

4. WB系数

$WB = k \times \frac{SSW}{SSB}$

原理同上，只不过现在是类内方差是分子，故结果是越小说明聚类效果越好。

指标选择原则

以上介绍的几个评价聚类的指标，并非是单调递增或者递减的，所以一定要结合多个参数交叉选择 $K$ 参数

算法优缺点分析

优点：
- 原理简单易懂
- 聚类效果中上
- 空间复杂度o(N)，时间复杂度o(I*K*N)
缺点
- 对离群点，如噪声敏感
- 易遗漏大小相差很大的类别（即大类别吞噬小类别）
- 并非全局最优

案例部分

算法优化

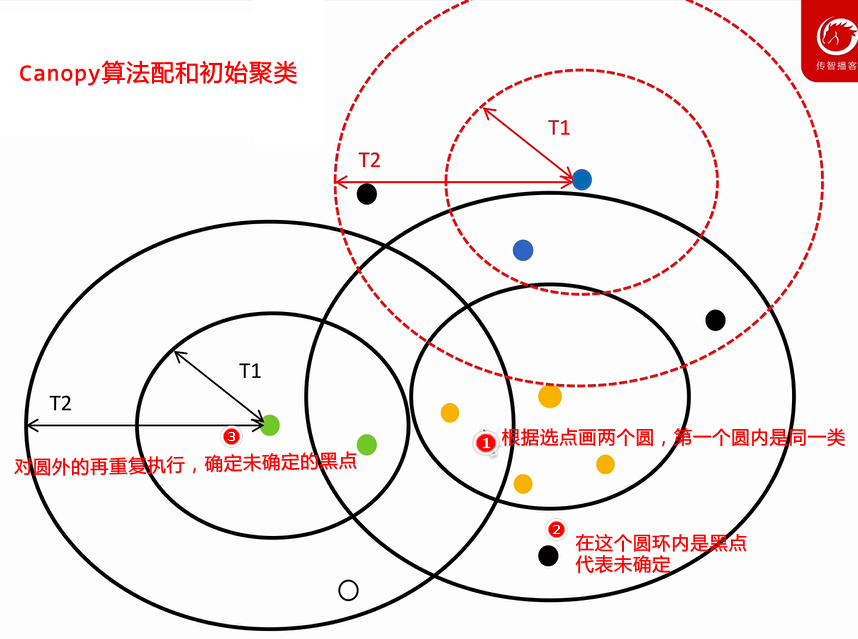
1. Canopy算法配和初始聚类

步骤：

随机选择一个点，绘制两个圆，半径分别是T1和T2
划分T1半径内的为同一类，T1和T2间的圆环内的为待定黑点，说明可能是同一类，也可能不是同一类。而对于T2外的点则判断肯定不是同类点。
对于T2外的原点重复1,2步骤。

(过程中可能将原先未确定的黑点做出判断)

优缺点分析：

Kmeans 对噪声敏感，通过Canopy可规定聚类中心的点，在T1半径内必须满足一定的点数，对于不满足点数的聚类中心直接去除，有利于解决噪声的干扰问题。
Canopy选择出来的 $K$ 值会更加精准。
只是对每个Canopy的内部进行Kmeans聚类，而非对整体做Kmeans聚类，计算量减少

缺点：

超参数需要手动确定 T1和T2

2. Kmeans ++

原理：做质心选择的时候，尽可能的远。

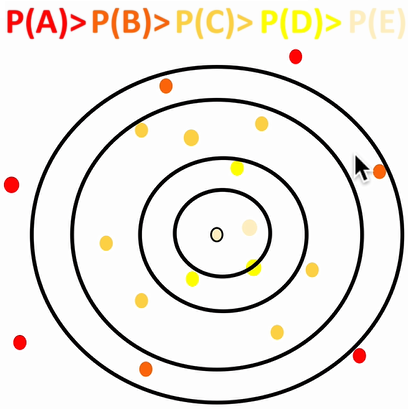
质心的选择通过概率控制：

$P = \frac{D(x)^2}{\sum_{x\in X}D(x)^2}$

其中：

分子部分是：待选择的质心到上一个质心的距离
分母部分是：所有点到上一个质心的距离

3. 二分K-means

算法步骤：

所有点作为一个簇
将簇一分为二
选择最大限度降低降低SSE（误差平方和）的簇去划分两个簇
重复2,3两步，知道簇的数目等于用户给定的数目

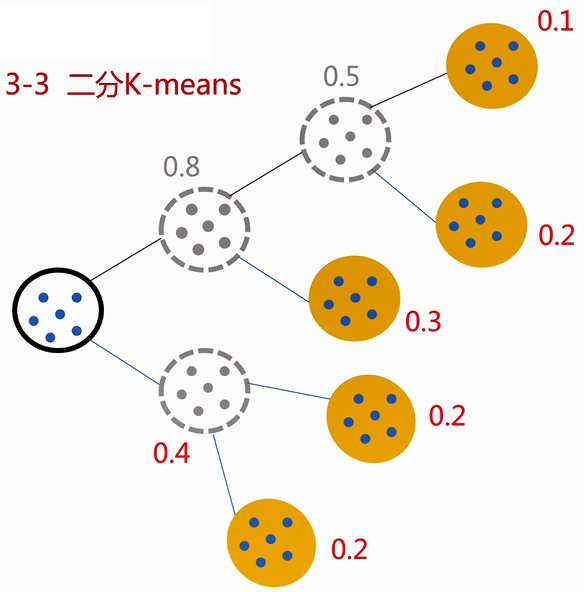
优缺点分析：

可以加速Kmeans的执行速度
过程中不存在随机性，结果唯一

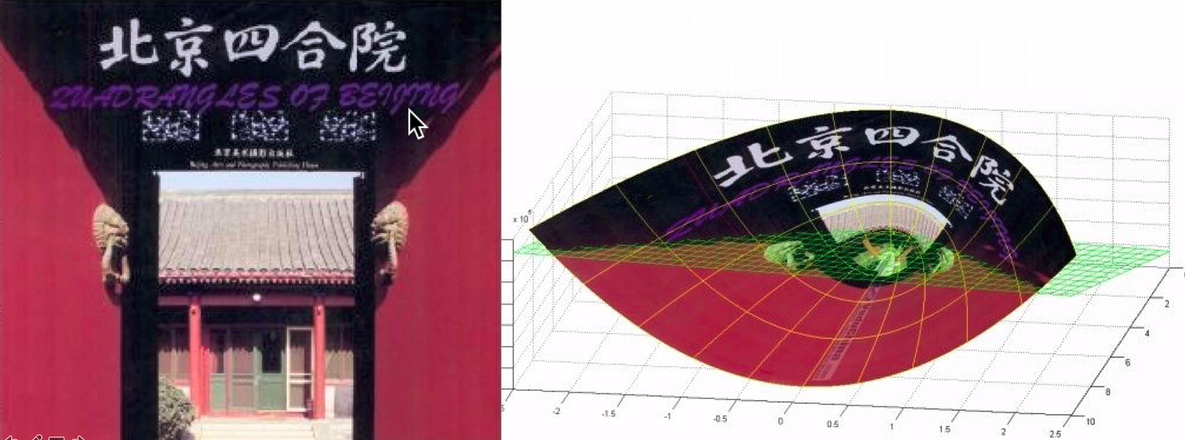
4. Kernel - Kmeans

解决：线性不可分的问题。主要利用了核方法的技巧，把低维数据映射到高维空间再利用Kmeans做一次聚类。

如区分下图中红色和黑色块的部分：

算法比对：

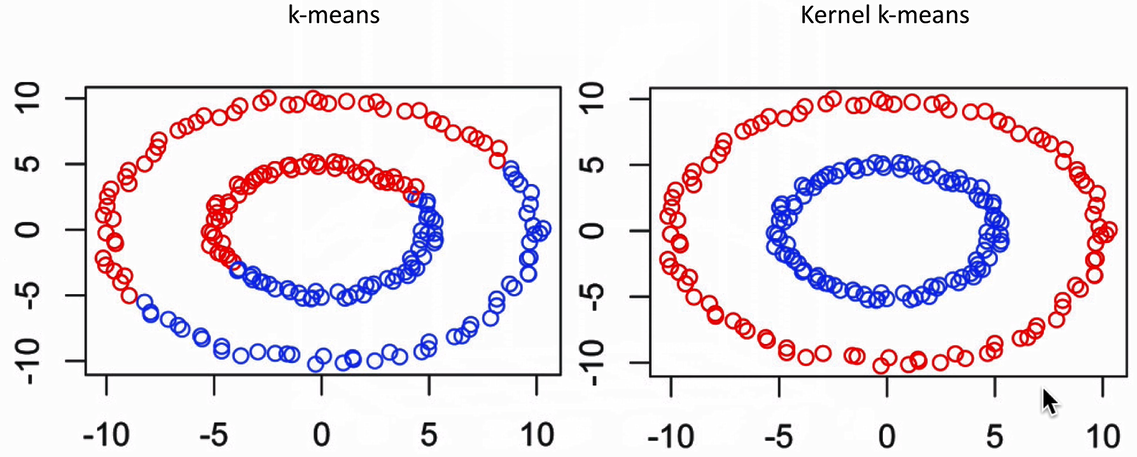
优缺点分析：

适合线性不可分的场景
计算复杂度高

5. K-medoids(K-中心聚类算法）

解决：K-means对异常值的敏感

K-medoids和K-means是有区别的，不一样的地方在于中心点的选取：

K-means中，将中心点取为当前簇中所有数据点的平均值，对异常点很敏感！【虚拟计算点】
K-medoids中，将从当前簇中选取到其他所有本簇内点的距离之和最小的点作为中心点。【实际样本点】

注：这里的距离用的是曼哈顿距离。

算法部步骤：

随机选择K个点作为medoids
聚类：将剩余的n-k个点分配到最佳的medoids
根据曼哈顿距离重新计算中心
迭代更新中心点，直至最大迭代数

优缺点：

噪声鲁棒性好
计算量大，建议小样本
虽然说初始中心都是随机选择的，但是随机性相对于Kmeans小很多，基本上每次运行程序得到的结果差不多。注：但是与Kmeans都是局部最优解。

6. ISODATA

全称：Iterative Self Organizing Data Analysis Techniques Algorithm

特点：自适应确定 $K$ 的个数，最终聚类中心的个数在一个范围内: $[K/2,2K]$

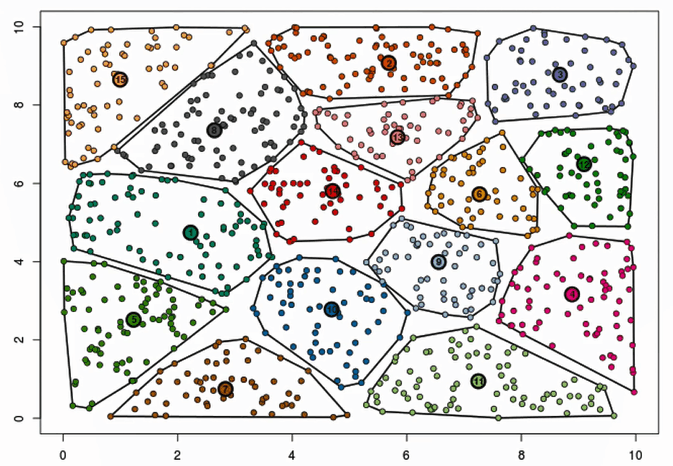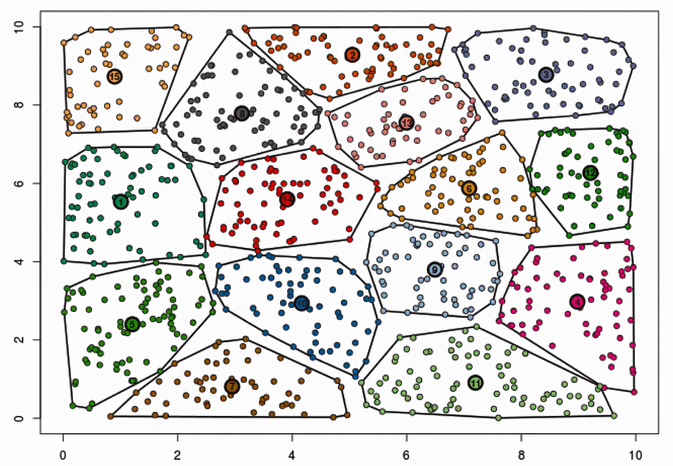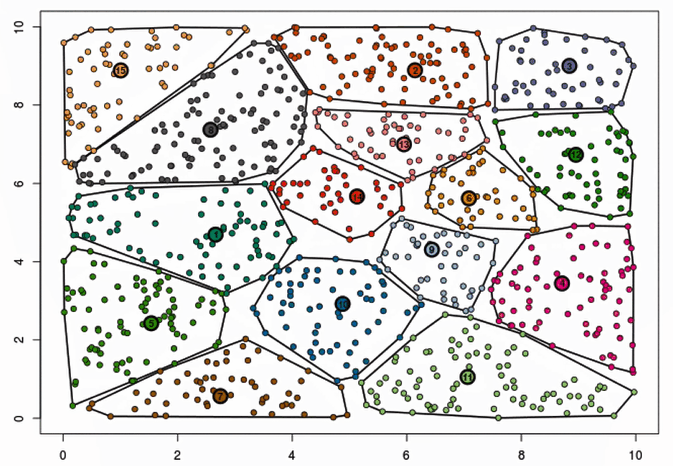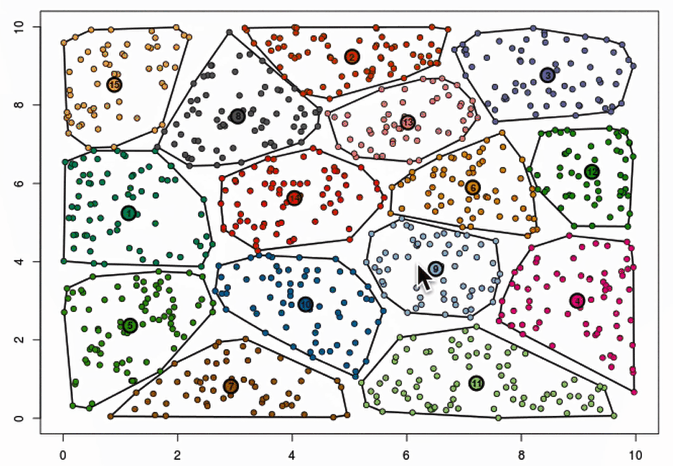
核心原理：

合并：当某一个类的样本个数太少，或者两个类的距离太近可视为一类
分裂：当某一个类的类内方差太大，则将该类进行分裂

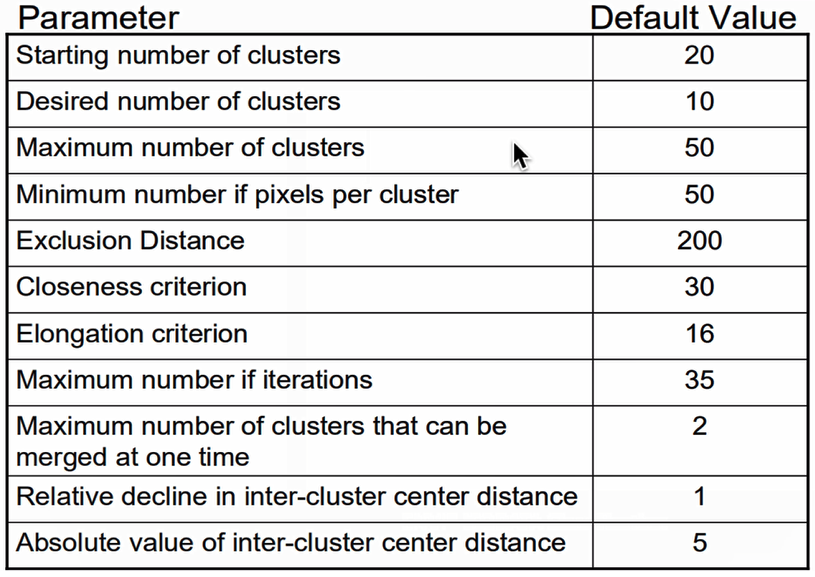
可选参数：

因ISODATA多用于遥感卫星图像的处理，所以输入的参数与Pixels有关。

高阶聚类算法

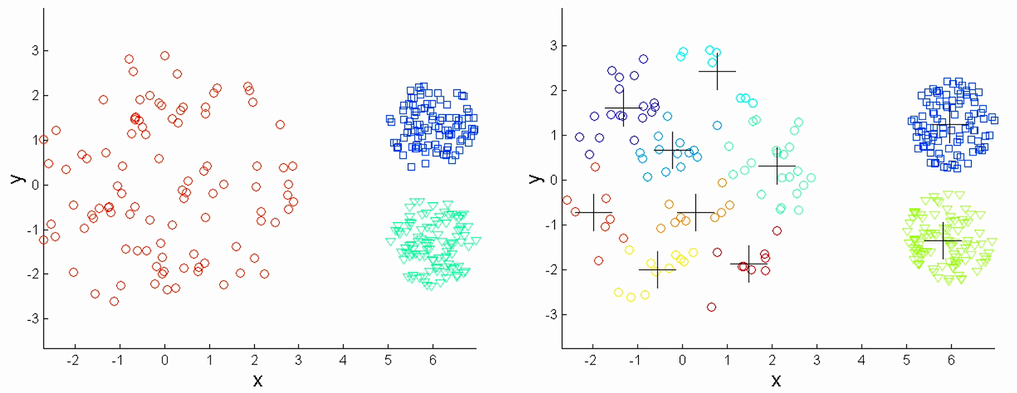
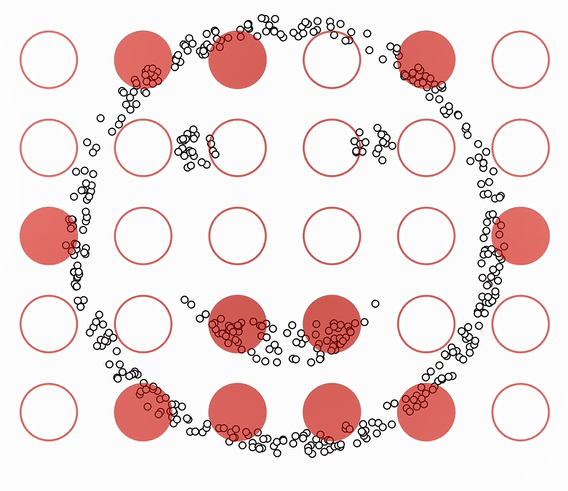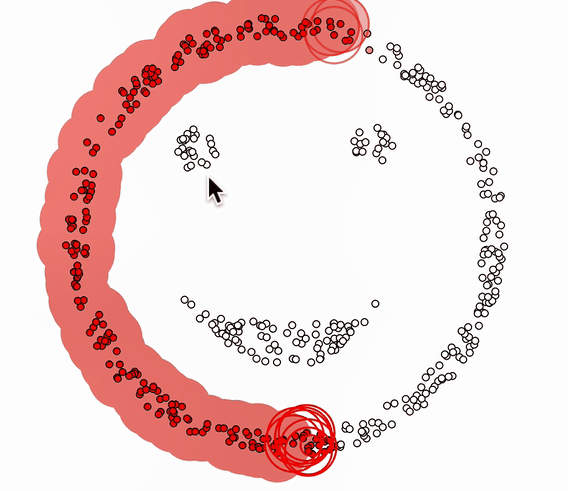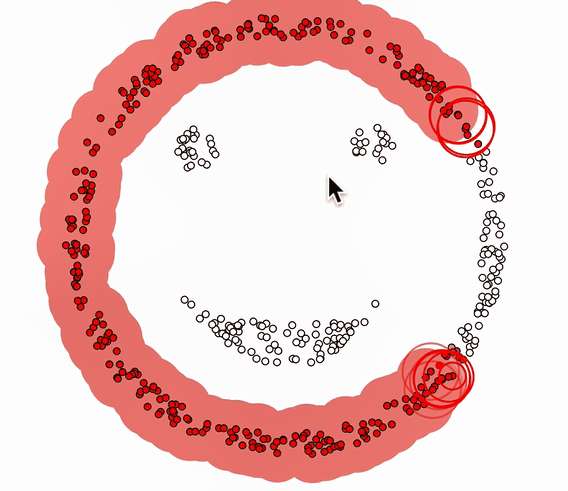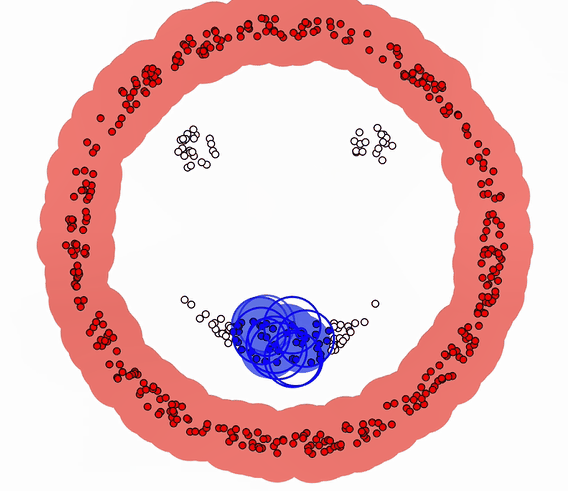
DBSCAN（密度聚类）

Kmeans聚类失败的案例：

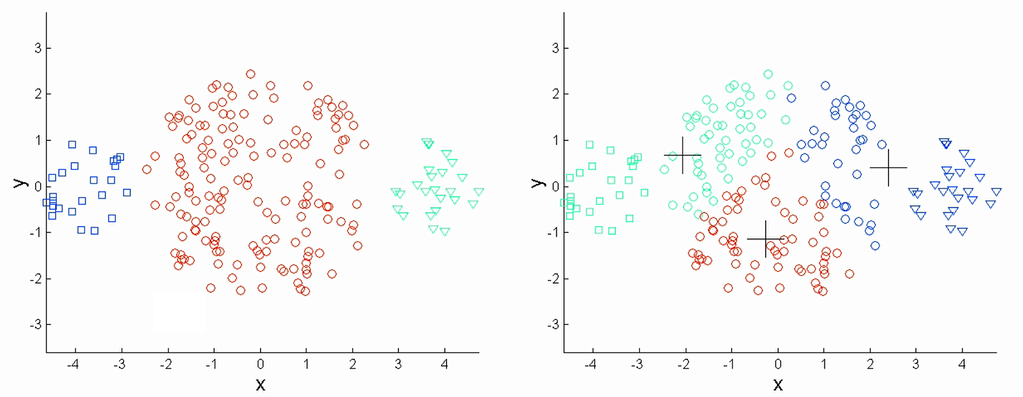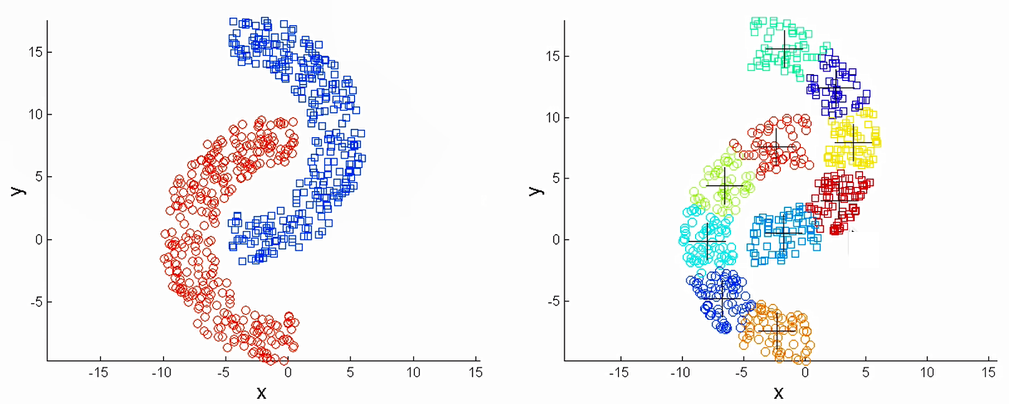聚类过程演示：

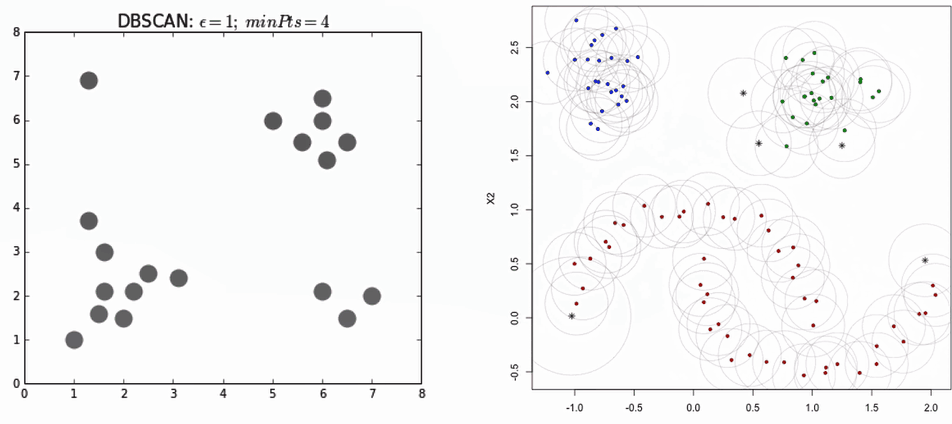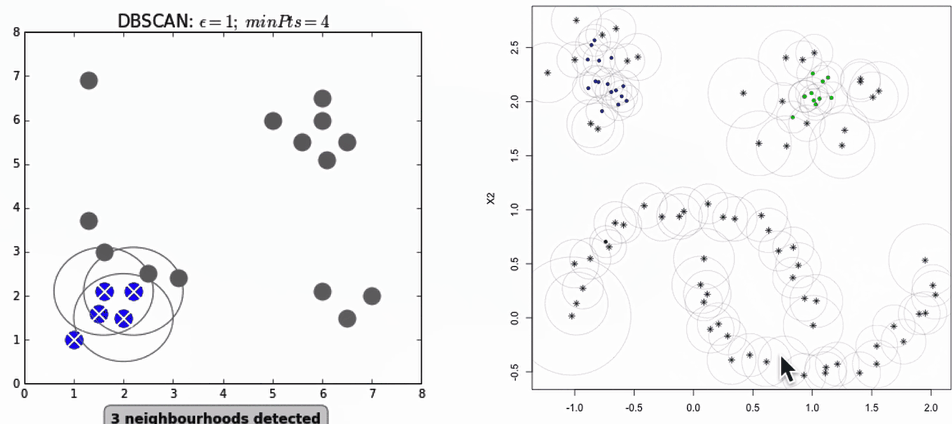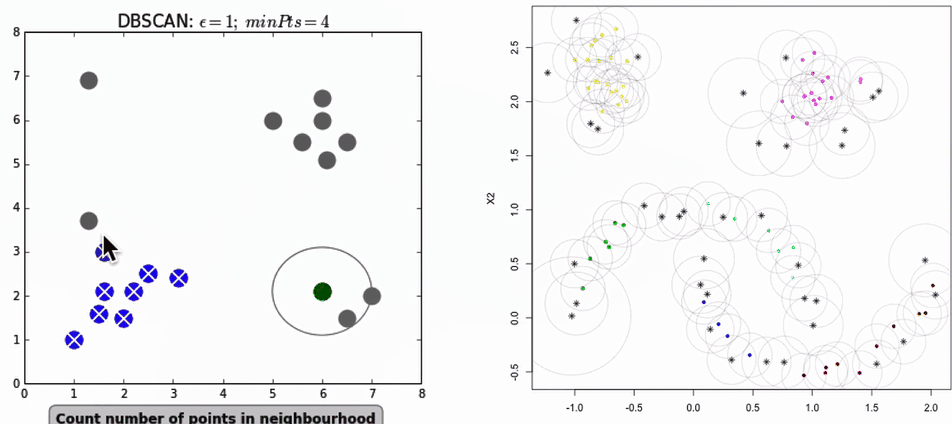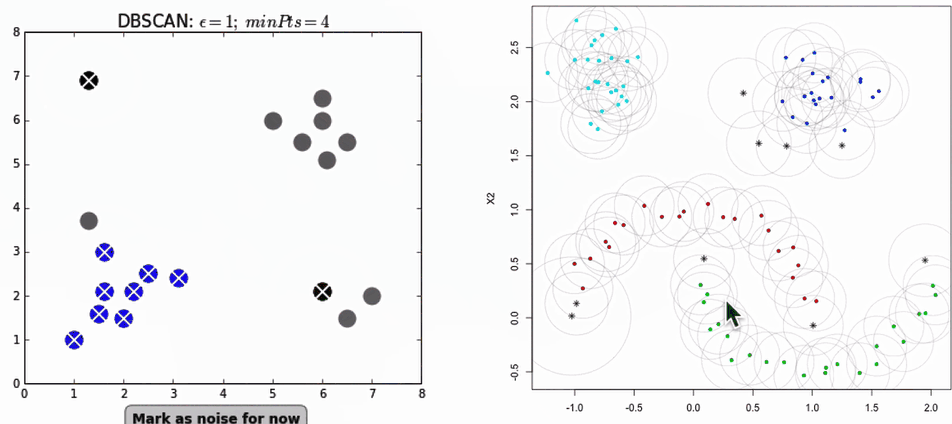
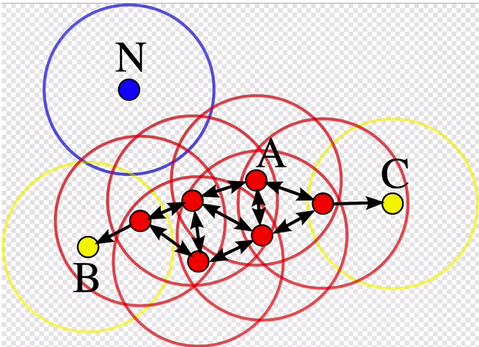
专业名词：

点的名称
- 核心点（需要满足一定的点）
- 边界点
- 噪声点
过程名称
- 密度可达
- 密度相连

算法缺点：领域的不同可能创造更多的噪声点：

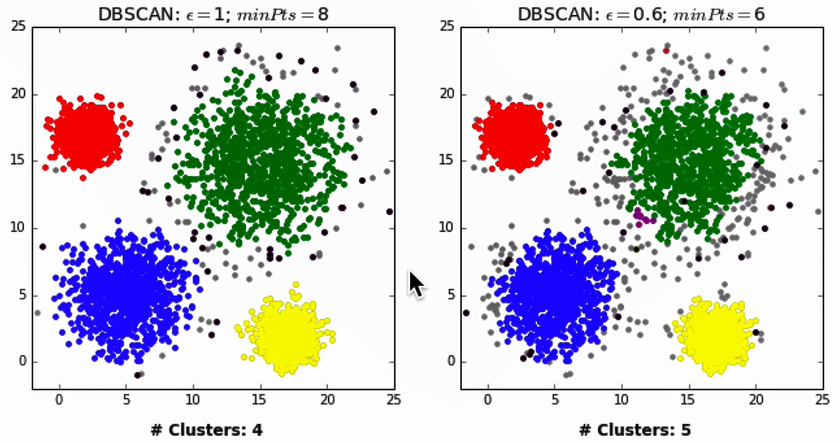优缺点分析：

优点	缺点
1. 聚类速度快，且能有效处理噪声，可以对任意形状的聚类	1. 数据量增大的时候，需要较大内存才能完成操作
2. 自适应聚类个数	2. 当不同类别密度差距大，超参数领域的大小和点数的设定比较困难
	3. 对于高维数据存在“维度灾难”

层次聚类

聚类的步骤：

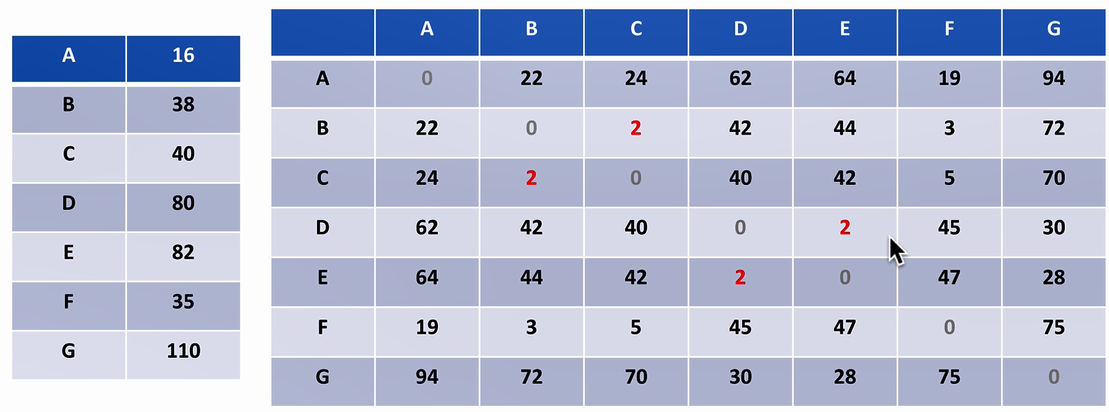
计算距离表格
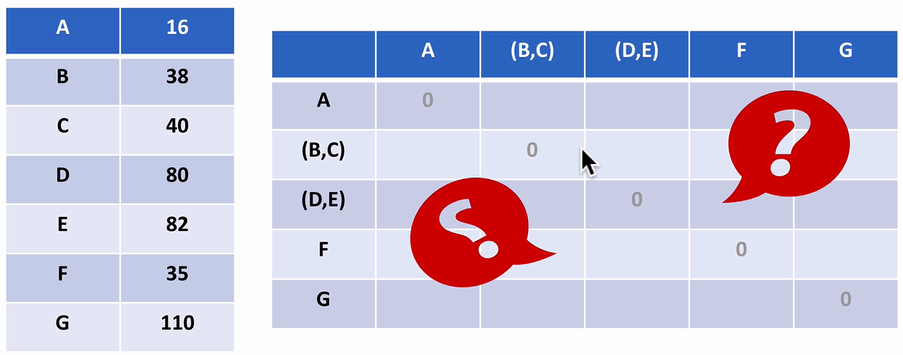
找到上面表格中聚类最近的两类，合并，再重复1的步骤

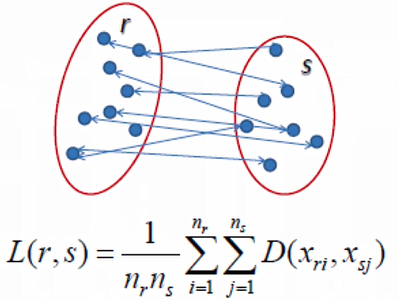
如何度量两个类之间的距离？

MIn度量

MAX度量

平均距离度量

质心度量

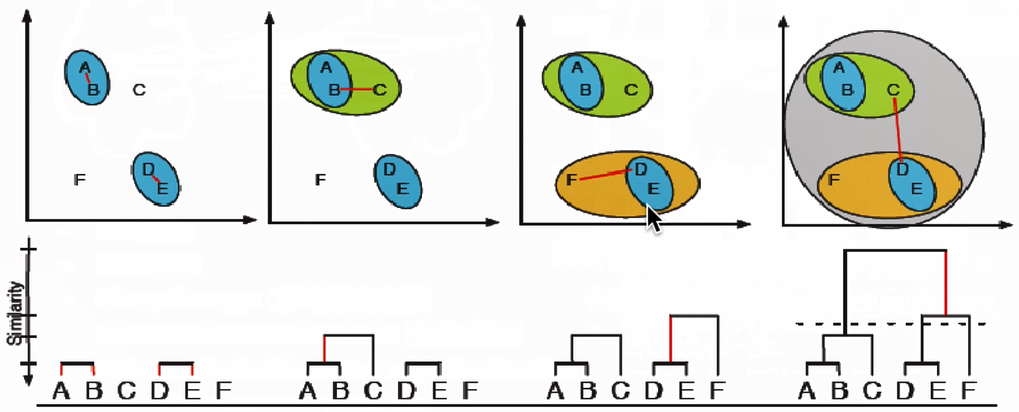
合并的时候需要记录两个类之间的距离：

红线计算的是合并前两个类别的距离，把计算的值作为聚类图的竖线。

优缺点：

优点
1. 不需要预先指定聚类数
2. 可以发现类的层次关系
缺点：
1. 计算复杂度高
2. 易产生链状聚类

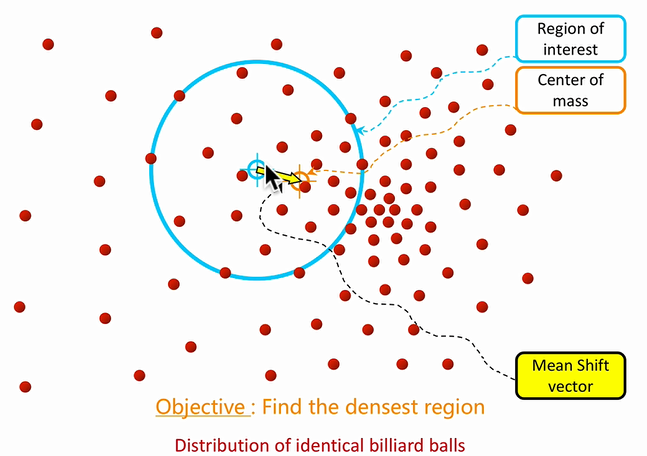
Mean Shift聚类

多用于动态捕捉

算法步骤：

设置一堆标记点**(非样本点)**，随机选择一个作为中心开始
计算半径为 $r$ 的圆内的向量的合方向作为移动方向
移动中心，重新就算向量的合方向
移动终止条件：shift的距离小于阈值停止，记录聚类中心center，以及移动路径中所有的点都归为此类
复核：重复上述1,2,3,4步骤，如果此时的center小于阈值则视为一类，若大于阈值则为不同类。直至所有的标记点被访问过一遍。
归类：因为不同的标记的点可能多次途径样本点，取访问频率最大的类作为当前样本点的类别。

注意事项：

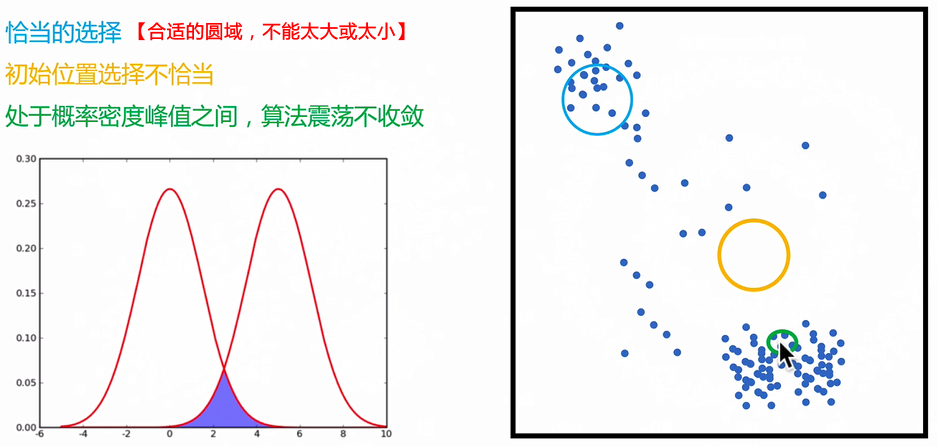
AP聚类

Preference参考度或者偏好参数：是相似度矩阵中横轴纵轴索引相同的点，如 $S(i,i)$ ，若按欧氏距离计算其值应为0，但在AP聚类中其表示数据点 $i$ 作为聚类中心的程度，因此不能为0。迭代开始前假设所有点成为聚类中心的能力相同，因此参考度一般设为相似度矩阵中所有值的最小值或者中位数，参考度越大则说明这个数据点成为聚类中心的能力越强，最终聚类中心的个数很可能也越多。

AP算法需要注意的点：

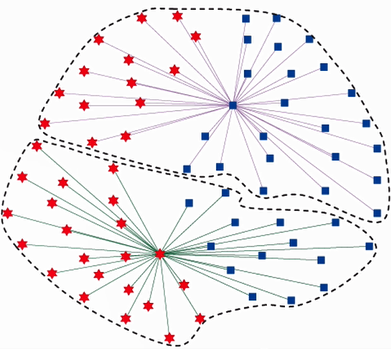
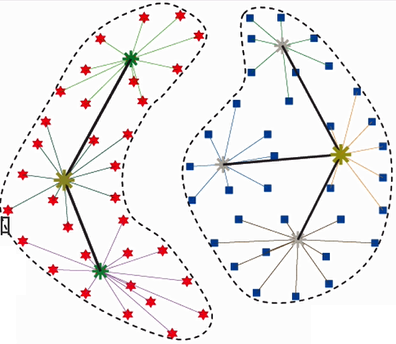
聚类结果需要进一步分析

不同的中心可为同一类	结构如：类树叉

不一定收敛

优缺点：

不需要设置聚类的个数，由Preference决定
由已有的点作为聚类的中心

缺点：

需要计算所有点的相似度，需要大内存
复杂度高 $o(N^3)$
受Preference和阻尼系数影响大

SOM聚类

基本原理：模拟人脑处于不同区域的神经细胞分工不同，即不同区域具有不同的相应特征。

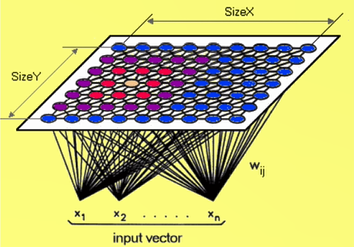
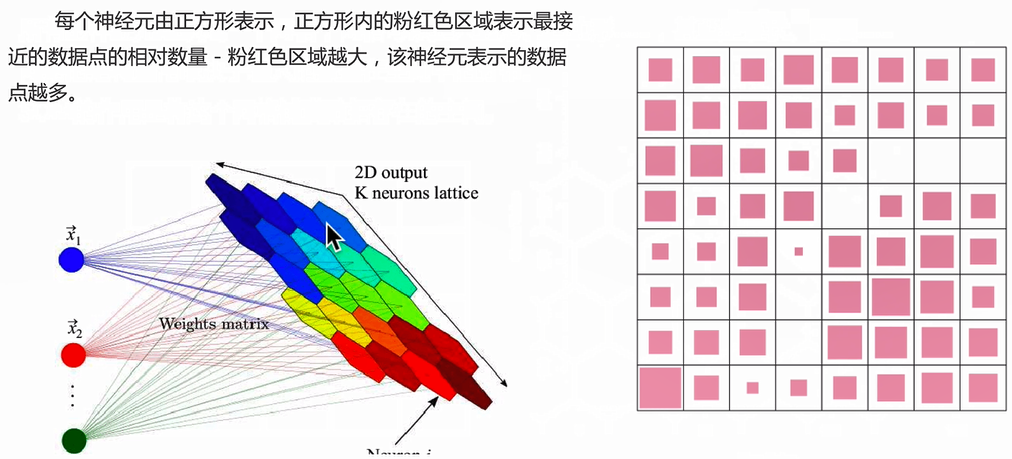
SOM神经网络的全称是Self Organizing Maps (SOM)自组织映射。其学习路径是先由对抗（竞争）网络的基础上发展出来的。但是SOM多了一个东西就是其映射保留了输入特征的拓扑特性。什么意思呢？加入说原先有个向量是 $X = \{x_1,x_2,\dots,x_D\}$ 这里是 $D$ 是指维度。理论上机器学习中默认所有的变量是独立的，或者说是无序的。即 $X = \{x_1,x_2,\dots,x_D\}$ 和 $X = \{x_D,\dots,x_2,x_1\}$ 训练出的结果是一样的。但是若是考虑了input向量的拓扑结果，则可能最终的分类结果是完全不同的。

SOM为了保留输入向量的拓扑结构，构造了一个竞争层，一般为二维网格平面(也称Kohonen Network，因为SOM的提出者是芬兰神经网络专家Kohonen教授)，网格点即为神经元，点与点之间保持一定的结构关系（即拓扑）。这里的竞争层就是原先的输出层，只不过这里用SOM做聚类任务，无需输出。(传统神经网络输出值的主要目的是为了做回归任务)。总结SOM就是一个单输出，单输出无隐藏层的神经网络结构。

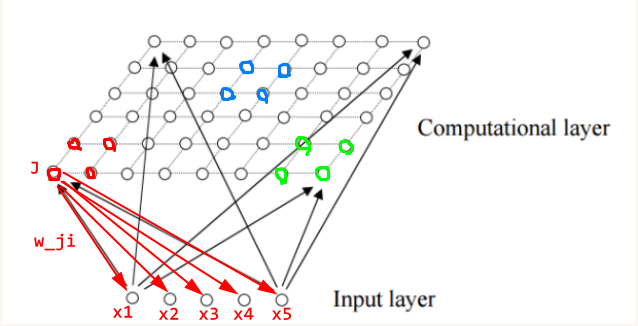
具体步骤如下：

初始化：每个节点开始初始化所有自己的参数 $w_{j(\cdot)}$
竞争：对于每一个输入数据，找到与它最相配的节点。假设输入时D维的，即 X={x_i, i=1,…,D}，那么判别函数可以为欧几里得距离：

$d_j(x)=\sum_{i=1}^D(x_i-w_{ij}^2)$

因为权重是随便设置的，所以一开始样本 $x^{(i)}$ 可能随机匹配到上述网格中其中某一个神经元结点。那下一步我就强化这一点与第一个样本向量之间的关系，那么下一次再来一个与此样本相似的向量时，会优先选择此前激活过的神经元范围内的结点。

还有就是一开始邻域的范围很大，可能占到半个数据集，后面慢慢缩小。

具体做法：就是让权重更靠近。
每一次迭代，一个样本只能与一个神经元有关系，赢者通吃。获胜单元及其邻域内的神经元开始向这个输入向量靠近。更新权重有一个原则，激活节点神经元与输入向量权重更近，周围的邻域内的神经元根据距离的远近更新权重。

首先定义邻域：

$T_{j,I(x)}=exp(-\frac{S^2_{j,I(x)}}{2\sigma^2})$

可以发现T的取值范围是 $[1,0)$ , $S_{ij}$ 表示节点i和j之间的距离。可以发现距离越远，T的值越小。接下来更新节点的权重参数了，现在 $x_i$ 与 $w_{ji}$ 还差 $(x_i-w_{ji})$ 就完全相等了，当然不能一次性全部更新完，所以需要设置一个学习率 $\eta(t)$ 。T的目的则是再加上一个系数减少更新程度。

$\Delta w_{ji}=\eta(t)T_{j,I(x)}(t)(x_i-w_{ji})$
提供新样本，重复上面的操作
随着epoch的进行，需要不断的收缩邻域的半径，减少学习率，重复，知道小于允许值，输出聚类结果。

文献下载地址：http://www.cs.bham.ac.uk/~jxb/NN/l16.pdf

SOM聚类的步骤：

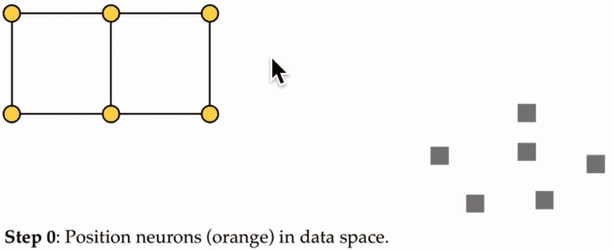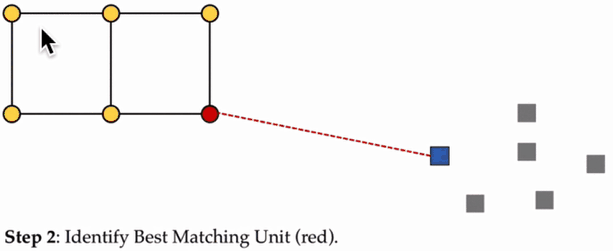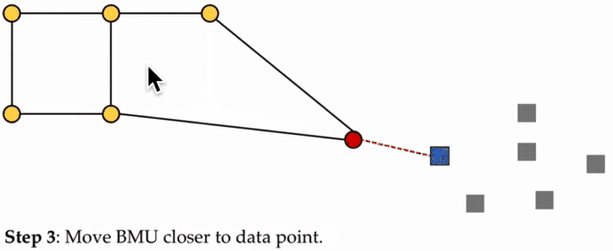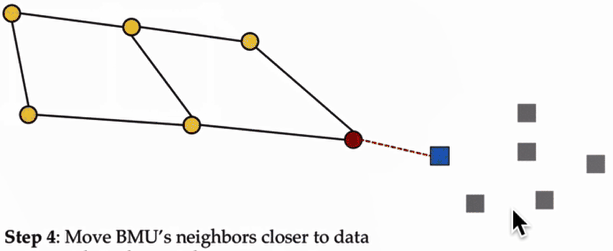
SOM的训练过程：
紫色区域表示训练数据的分布状况，白色网格表示从该分布中提取的当前训练数据。
（1）SOM节点位于数据空间的任意位置，最接近训练数据的节点（黄色高亮部分）会被选中。它和网格中的邻近节点一样，朝训练数据移动。
（2）在多次迭代之后，网格倾向于近似该种数据分布（下图最右）。

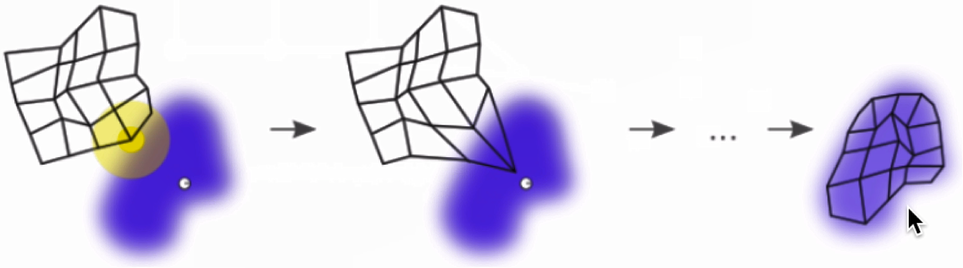
所有神经元组织成一个网络，网格可以是六边形，四边形，甚至是链形。网格的结构通常取决于输入的数据在空间中的分布。SOM的作用是将网格铺满数据存在的空间。

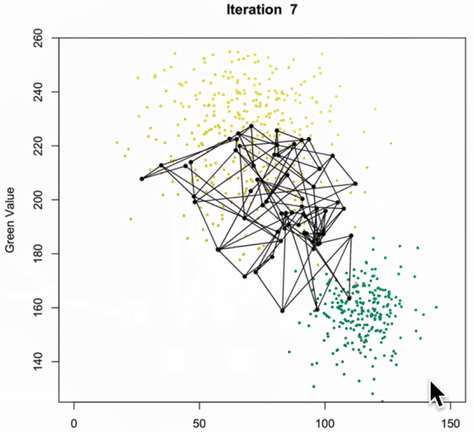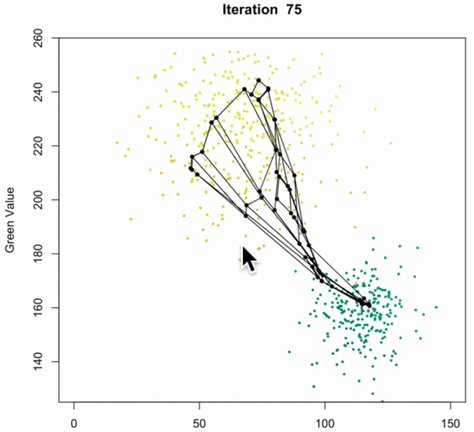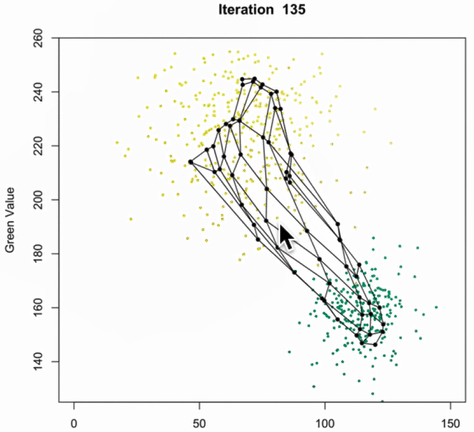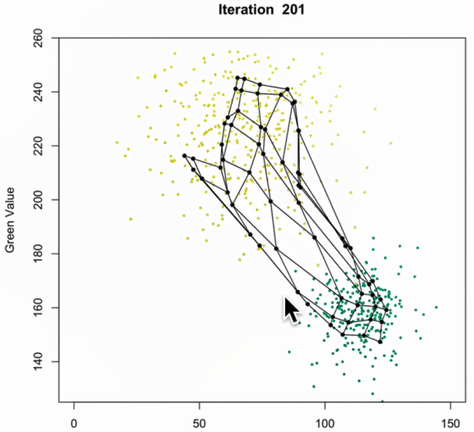
特点：

SOM无需提前设置聚类的数目。
SOM受极端值的影响要小于K-means。

下面是一个Maltab实践SOM神经网络的小的Demo代码

%% I. 清空环境变量
clear all
clc
%% II. 训练集/测试集产生
%%
% 1. 导入数据
% load water_data.mat
mu = [0,2 ; 5,6 ; 9,10];%数学期望
sigma = [1,0;0,4];%协方差矩阵
r1 = mvnrnd(mu(1,:),sigma,100);%生成50个样本
r2 = mvnrnd(mu(2,:),sigma,100);%生成50个样本
r3 = mvnrnd(mu(3,:),sigma,100);%生成50个样本
P_train = [r1;r2;r3]';

%% IV. SOFM神经网络创建、训练及仿真测试
% 1. 创建网络
net = newsom(P_train,[3 1]);
% 2. 设置训练参数
net.trainParam.epochs = 200;
% 3. 训练网络
net = train(net,P_train);
% 4. 仿真测试
 
% 训练集
t_sim_sofm_1 = sim(net,P_train);
T_sim_sofm_vec2ind = vec2ind(t_sim_sofm_1);  %向量和稀疏矩阵之间转换

% 测试集
t_sim_sofm_2 = sim(net,P_test);
T_sim_sofm_vec2ind  = vec2ind(t_sim_sofm_2);

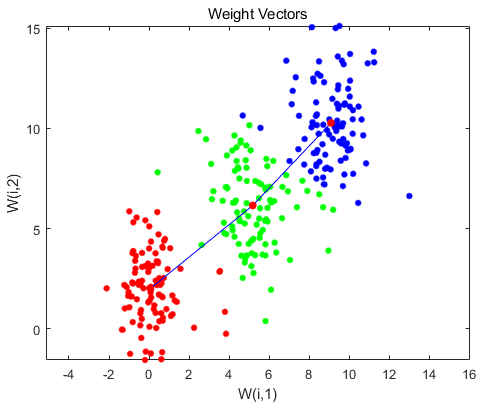
运行完上面的程序，观察网络的神经元的位置

figure
plot(P_train(1,:),P_train(2,:),'.g','markersize',20)
hold on
plotsom(net.iw{1,1},net.layers{1}.distances)
hold off

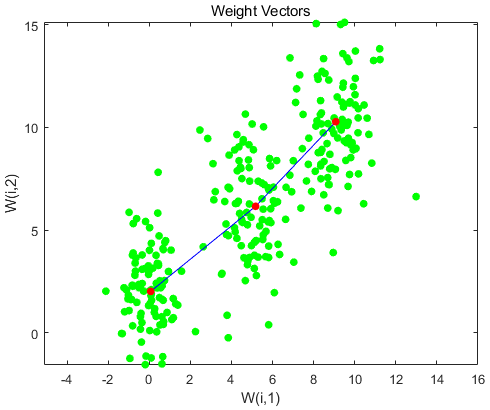
计算某个样本和所有权重的欧氏距离，划分这个样本为距离最近的权重所代表的的神经类别。

distances = dist(P_train',net.IW{1}');
[d,cndx] = min(distances,[],2); % cndx contains the cluster index
figure
gscatter(P_train(1,:),P_train(2,:),cndx); legend off;
hold on
plotsom(net.iw{1,1},net.layers{1}.distances);
hold off

谱聚类

基于图论的聚类方法，通过对样本数据的拉普拉斯矩阵的特征向量进行聚类。

视频链接：B站视频

案例部分

K-means 与 DBSCAN聚类效果比较：

https://www.bilibili.com/video/av44274148?p=44
综合实践：聚类算法的客户价值分析

https://www.bilibili.com/video/av44274148?p=47

聚类算法的其余簇评价指标：ROC、混淆矩阵