Matlab编程 – LDA实现

LDA原理说明

参考资料：https://blog.csdn.net/JackyTintin/article/details/79803501

$LDA$ 其实很好理解，全称是线性判别分析(Linear Discriminant Analysis)，是一种有监督算法。对其公式的推导，一般的书中都是以降维为目的的，所以经常会和PCA混为一谈，甚至搞混，不知道什么时候用PCA或者LDA。其实区分很简单，PCA保证的是数据的投影误差最小，即从最小二乘的误差的角度，投影前和投影后的向量有多"像"。而 $LDA$ 则多考虑一层，即数据的类别，希望投影后便于分类。

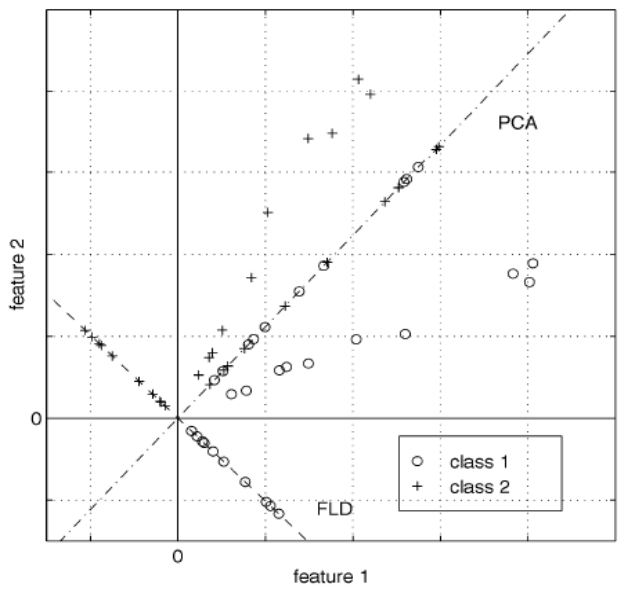
从上图可以发现PCA投影后的数据与原数据的误差是很小的。而LDA则完全不考虑这种**"空间"上的误差，只要求投影后的特征好区分即可。故为了分类**的目标衍生了两种的算法。第一，直接得到分类的决策面。第二，直接找到投影方向，分类的任务后续再做。

1. 目标：分类决策平面（线性）

此算法中 $LDA$ 假设数据服从高斯分布，并且各类的协方差相同【可以观察下图(二维平面)中椭圆的形状相同】，至于为什么要求分布必须是长相相同的椭圆？请看下述分析。

如果各类的先验概率为 $\Pi_k$ ，其中 $\sum_k\Pi_k = 1$ ，则数据的概率分布为：

$p(x|k)\backsim N(\mu_k,\Sigma )$

后验概率：

$p(k|x) = \frac{p(x|k)\Pi_k}{p(x)}$

⭕️直接构建分类决策平面：【直接比较后验概率的比值，取对数后，大于0代表分子的概率大于分母的概率】

$\begin{aligned} \ln \frac{p(k | x)}{p(l | x)}& =\ln \frac{p(x | k)}{p(x | l)}+\ln \frac{\pi_{k}}{\pi_{l}} \\&=\ln \frac{\pi_{k}}{\pi_{l}}-\frac{1}{2}\left(\mu_{k}-\mu_{l}\right)^{T} \Sigma^{-1}\left(\mu_{k}+\mu_{l}\right)+x^{T} \Sigma^{-1}\left(\mu_{k}-\mu_{l}\right) \\ & = A + x^T*B \end{aligned}$

上面的第二行等式中，只有协方差相同才可以合并。

为什么一定要进行合并操作？因为只有合并后，最终得到的分类界面是线性的，这里有个前提就是要求方差相同，即 $\Sigma$ 相同

**对数似然值是关于 $x$ 的一个线性函数。**若值大于0，则代表分子所代表的分布获胜，若小于0则分母所代表的分布获胜。

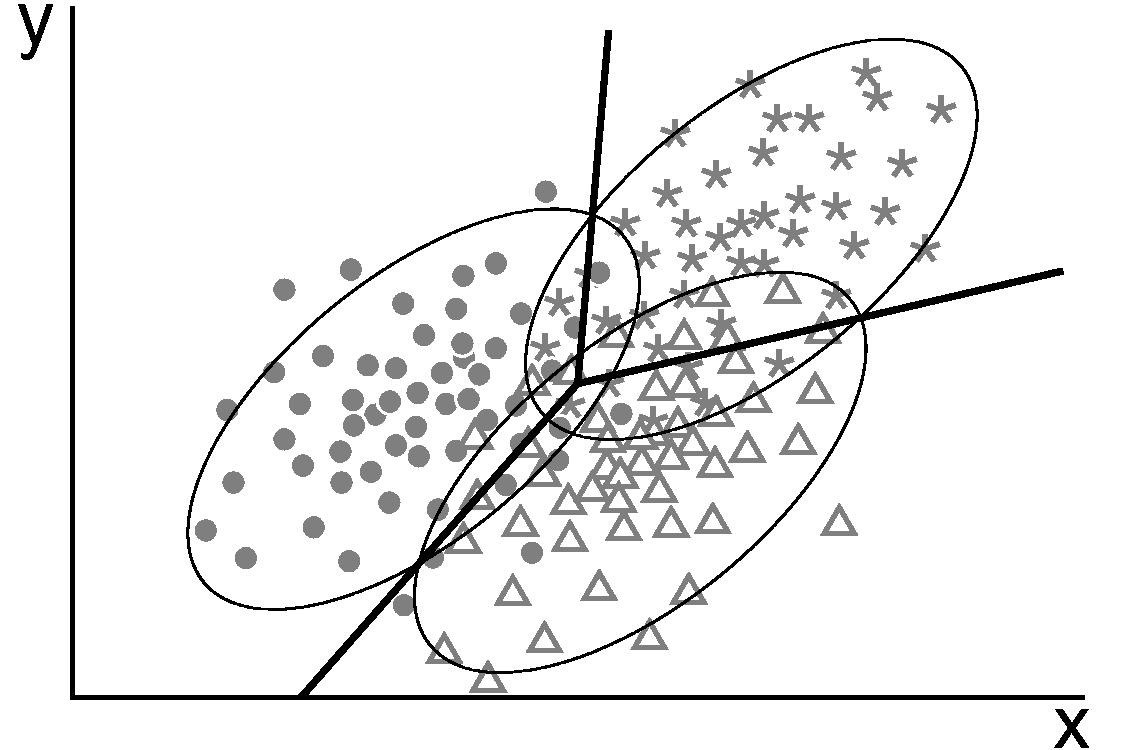
如果允许各类的协方差不同，则决策面是二次的，称为二次判别分析（QDA（Quadratic Discriminant Analysis，QDA））

2. 目标：降维 LDA

原理：高内聚松耦合

对于 LDA 降维还有另一种解释来自 Fisher：对于原数据 X，寻找一个线性组合 $Z = \omega^TX$ （低维投影），使得 $Z$ 的类间方差与类内方差的比值最大。

最终降维的维数取决于需要分类的目标数，与维度无关。

D维K类 --> K-1 维

分子：类间散度矩阵

$S_b = \sum_k n_k(m_k-m)(m_k-m)^T$

分母：类内散度矩阵

$S_w = \sum_k \sum_{i=c_k}(x_i-m_k)(x_i-m_k)^T$

算法推导：

优化瑞利熵（Rayleigh Quotient）

$w = argmax_{w}\frac{w^TS_bw}{w^TS_ww}$
等价

$w = argmax_w w^TS_bw \\ s.t. w^TS_ww = 1$
拉格朗日方法

$\mathbf{w}^{T} S_{b} \mathbf{w}-\lambda\left(\mathbf{w}^{T} S_{w} \mathbf{w}-1\right)=0$
求导

$2S_bw-\lambda(2S_ww)=0$
求导后

$S_b w = \lambda S_ww$
如果 $S_w$ 可逆，则有：

$S_{w}^{-1} S_{b} \mathbf{w}=\lambda \mathbf{w}$
进一步改写：

$\begin{aligned} w & = \frac{1}{\lambda}S_w^{-1}S_bw \\ &\propto S_w^{-1}S_bw \\ &\propto S_w^{-1}(\bar{x}_{c1}-\bar{x}_{c2}) \end{aligned}$

根据定义 $S_bw$ 中 $w$ 可以与 $S_b$ 中的某一部分约掉，见下说明

$\begin{aligned} S_b\mathbf{w} & = (\bar{x}_{c1}-\bar{x}_{c2})(\bar{x}_{c1}-\bar{x}_{c2})^T\mathbf{w} \\ (p,p)(p,1) & = (p,1)(1,p)(p,1) \\ & = (p,1)*(1,1) \end{aligned}$

注意的是，上面的常数都可以被约去，因为我们只关心它的方向，而并不关心具体的长度。

故在JF.m中的核心代码是：
- 先计算投影方向
- 再归一化投影值
%计算最佳投影方向向量
w=inv(Sw)*(m1-m2);%(p,p)*(p,1)=(p,1)
%将向量长度变成1
w=w/sqrt(sum(w.^2));

总结: 两种视角的比较

从概率生成角度进程决策面分类
- 主要用途是分类，决策面的个数主要取决于分类个数K，与维度无关。
Fisher视角:高内聚松耦合
- 主要的用途是降维
  - 如何找到投影的方向？

计算 $S_w^{-1}(\bar{x}_{c1}-\bar{x}_{c2})$

如何降维
- 计算 $S_w^{-1}S_b$ 的(p,p)维的特征向量，有p个特征值，就有p个特征向量。取前K个特征值所对应的特征向量即可

$W$ 的维度很关键，若X的维度是 $(p,1)$ ，而W代表空间通道 $(p,k)$ ，若此时k等于p，说明W起的矩阵乘的目的是旋转，或者拉伸的作用，投影后的向量还在原来的空间。若k小于p，才有降维的效果。

⭐️注意：公式推导中的w是(p,1)维的， $w^Tx$ 计算后的结果是一个实数，代表着向量的投影，物理意义是：老坐标在新坐标系下的坐标值。而W则代表着空间(p,k)，说明将老坐标系下的一个向量，往k个w上面投影下的坐标值。

可以观察下面的代码，可以对上面的解释有更深的理解：

cc1 =  w'*c1;
cc2 =  w'*c2;
% 若需要画图，需要将新坐标下的坐标再转换回原坐标系
% 联系的纽带就是，新坐标系坐标轴w在原坐标系下的坐标值。
cc1 = cc1.*w ;
cc2 = cc2.*w ;

维度筛选：Fisher比

摘自论文《基于Fisher分值的特征提取在语音确认中的应用》

特征选择是指从D维特征参数中挑选d（d<D）维最有效的特征以达到降低空间维数从而提高系统性能的目的，因此需要一个定量的标准来衡量特征参数对分类的有效性。在模式识别中，可以运用Fisher准则得到特征向量的最佳投影方向，在该方向投影可以使类间的分离度最大。Fisher准则最初是由R.A.Fisher于1936年在他的经典论文中提出的，其基本原理是找到特征空间的某个投影子空间，使所有特征点在该子空间得到最好的分类。1964年，Bel1实验室的Pmzansky和Matllews利用方差分析的方法进行说话人识别研究，在Fisher准则的基础上提出了衡量说话人特征参数有效性的F比公式。其定义为：

$F_{Fisher}=\frac{\sigma_{between}}{\sigma_{within}}$

$F_{Fisher}$ 为特征参数各维的Fisher比，它的值越大，表示某一维的可分离性越好。 $\sigma_{between}$ 为类间离散度矩阵，表示说话人之间第k维分量的类间方差之和，其数学表达式如下：

$\sigma_{\text {between }}=\sum_{i=1}^{M}\left(m_{k}^{(i)}-m_{k}\right)^{2}$

其中，M为说话人的个数， $m_k^{(i)}$ 表示说话人i的第k维分量的均值， $m_k$ 表示所有说话人第k维分量的均值。 $\sigma_{within}$ 为类内离散度矩阵，表示某个说话人第k维分量类内方差之和，其数学表示如式所示：

$\sigma_{\text {within }}=\sum_{i=1}^{M}\left[\frac{1}{n_{i}} \sum_{c \in n_{i}}\left(c_{k}^{(i)}-m_{k}^{(i)}\right)^{2}\right]$

其中， $n$ 为说话人i的样本数， $c_k^{(i)}$ 表示说话人 $i$ 的第 $k$ 维特征参数。

总结

类间方差：
- 计算的是一堆均值的方差
类内方差：
- 计算的是每类样本的方差，有两个求和，先计算一类样本中所有的方差和，为平衡不同类样本的方差，所以要除以每类样本的均值，最后对所有的类别的方差求和即可。

代码

自己写

创造样本 createSwatch.m

function swatch=createSwatch(xmin,xmax,ymin,ymax,num,varargin)
xlen=abs(xmax-xmin);
ylen=abs(ymax-ymin);
if numel(varargin)>0 && isa(varargin{1},'function_handle')
f=varargin{1};
else
f=@rand;
end
swatch=[xlen*f(1,num)+min(xmax,xmin);...
ylen*f(1,num)+min(ymax,ymin)];

分类判断JF.m

function w=JF(c1,c2)
%利用Fisher准则函数确定最佳投影方向
%c1和c2分别为两类样本的样本矩阵,（p,n）

m1 = mean(c1,2);
m2 = mean(c2,2); %(p,1)

%样本向量减去均值向量
c1=c1-repmat(m1,[1,size(c1,2)]);%(p,n)-(p,1)
c2=c2-repmat(m2,[1,size(c2,2)]);%(p,n)-(p,1)

%计算各类的类内离散度矩阵
%(p,n)*(n,p)=（p,p） 算法运算量为 n^2 而若是拆开计算可以节省计算量(p^2)
S1=c1*c1.';
S2=c2*c2.';

%计算总类内离散度矩阵
Sw=S1+S2; %(p,p)

%计算最佳投影方向向量
w=inv(Sw)*(m1-m2);%(p,p)*(p,1)=(p,1)
%将向量长度变成1
w=w/sqrt(sum(w.^2));

主程序代码

clear all;close all ;clc;
%定义两类样本的空间范围
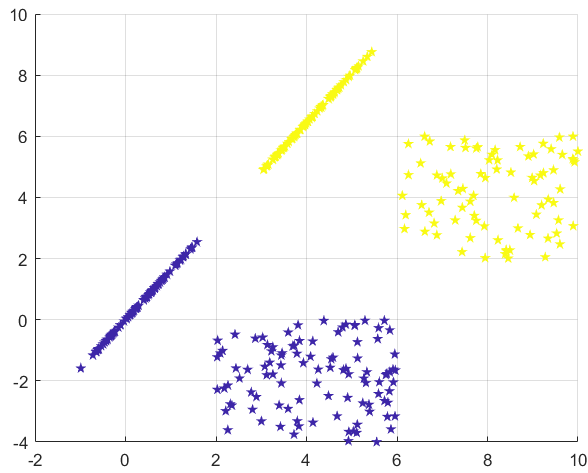
x1min=2;x1max=6;
y1min=-4;y1max=0;
x2min=6;x2max=10;
y2min=2;y2max=6;
%产生两类2D空间的样本
c1=createSwatch(x1min,x1max,y1min,y1max,100);
c2=createSwatch(x2min,x2max,y2min,y2max,80);
%获取最佳投影方向
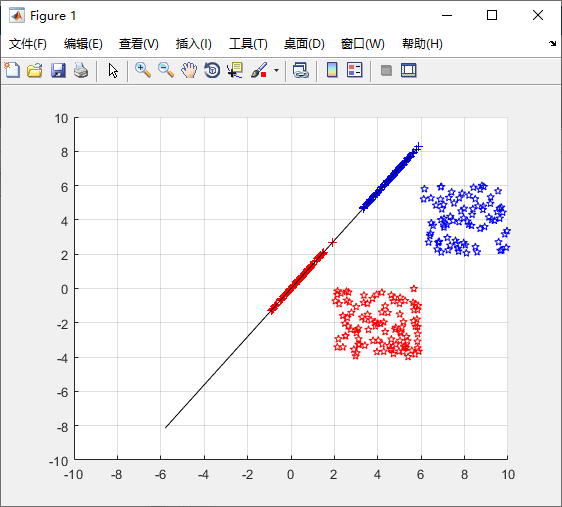
w=JF(c1,c2);
%计算将样本投影到最佳方向上以后的新坐标

cc1 =  w'*c1;
cc2 =  w'*c2;
% 若需要画图，需要将新坐标下的坐标再转换回原坐标系
% 联系的纽带就是，新坐标系坐标轴w在原坐标系下的坐标值。
cc1 = cc1.*w ;
cc2 = cc2.*w ;

%打开图形窗口
figure;
%绘制多图
hold on;
%绘制第一类的样本
plot(c1(1,:),c1(2,:),'rp');
%绘制第二类的样本
plot(c2(1,:),c2(2,:),'bp');

%绘制第一类样本投影到最佳方向上的点
plot(cc1(1,:),cc1(2,:),'r+');
%绘制第二类样本投影到最佳方向上的点
plot(cc2(1,:),cc2(2,:),'b+');

w=10*w;
%画出最佳方向
line([-w(1),w(1)],[-w(2),w(2)],'color','k');
axis([-10,10,-10,10]);
grid on;
hold off;

调轮子

clear all;close all ;clc;

% 生成数据
[c1,c2] = generate_dots();

%根据lda的要求准备数据
Ind = [ones(size(c1,2),1);repmat(2,[size(c2,2),1])]; 
classes = ["r";"b"] ;
X = [c1 ,c2] ; 
X_label = classes(Ind) ;

% 降维
[V,D] = lda(X, X_label);

% 投影数据
ccc1 = V'* X ;

% 根据投影数据返投回原坐标系
ccc1 = ccc1.* V ;

% 绘图：
plot_2D_star(ccc1,X,Ind)

function swatch=createSwatch(xmin,xmax,ymin,ymax,num,varargin)
xlen=abs(xmax-xmin);
ylen=abs(ymax-ymin);
if numel(varargin)>0 && isa(varargin{1},'function_handle')
   f=varargin{1};
else
    f=@rand;
end
swatch=[xlen*f(1,num)+min(xmax,xmin);...
    ylen*f(1,num)+min(ymax,ymin)];
end

function [c1,c2] = generate_dots()
%定义两类样本的空间范围
x1min=2;x1max=6;
y1min=-4;y1max=0;
x2min=6;x2max=10;
y2min=2;y2max=6;
%产生两类2D空间的样本
c1=createSwatch(x1min,x1max,y1min,y1max,100);
c2=createSwatch(x2min,x2max,y2min,y2max,80);
end

function plot_2D_star(ccc1,X,Ind)
figure;
scatter(ccc1(1,:),ccc1(2,:),50,Ind,'filled','Marker','p')
hold on 
scatter(X(1,:),X(2,:),50,Ind,'filled','Marker','p')
grid on 
xlim([-2,10]);
ylim([-4,10]);
set(gcf,'color','w')
end