本篇内容主要来源于白板书推导
背景介绍
- 过拟合
- 增加Data
- 正则化
- 降维
- 直接降维:
特征选择
- 线性降维:
PCA、MDS
- 非线性降维:流形
LSOMAP、LLE
- 维度灾难
预备知识
基础知识
-
数据:
x=(x1⋯xn)nxpT=⎝⎜⎜⎜⎛x1Tx2T⋮xnT⎠⎟⎟⎟⎞=⎝⎜⎜⎜⎛x11x21⋮xn×1x12x22⋮xn×2⋯⋯⋮⋯x1px2p⋮xn×p⎠⎟⎟⎟⎞
-
期望:
xˉ=21i=1∑Nxi
-
方差:
Sp×p=N1i=1∑N(xi−xˉ)⋅(xi−xˉ)T
推导技巧
-
技巧:
xˉ=N1i=1∑Nxi=N1(x1,x2,…,xn)⋅⎝⎜⎜⎜⎛11⋮1⎠⎟⎟⎟⎞=N1xT⋅1n
(x1−xˉ,x2−xˉ,…,xn−xˉ)=(x1,x2,…,xn)−xˉ⋅(1,1,…,1)=xT−N1xT⋅1N⋅(1N)T=xT(In−N1⋅1N⋅(1N)T)=xT⋅HN=H⋅x
H的性质:
-
易证:HT=H
-
H2=H⋅H=H
证明:
H2=(In−N11n⋅(1n)T)⋅(In−N11n⋅(1n)T)T=In+N211N1NT1N1NT−N21N1NT=In−N11N1NT=H
推广有:
HN=H
⭕️根据上面的技巧改写期望和方差公式:
xˉSp×p=N1xT⋅1n=N1xTH⋅(xTH)T=N1xTHx
主成分分析原理(PCA)
Principal Component Analysis
-
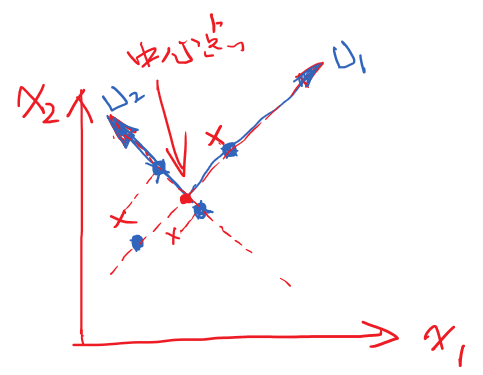
一个中心
-
两个基本点
-
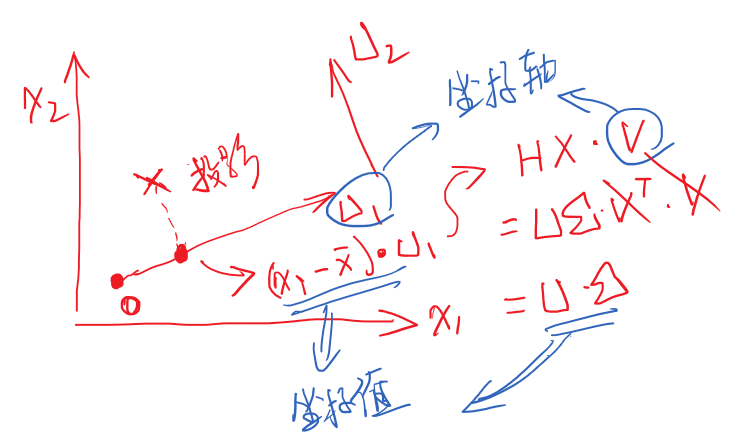
最大投影方差角度
-
最小重构距离【还原后的数据与原数据的差距最小】
![]()
最大投影方差角度
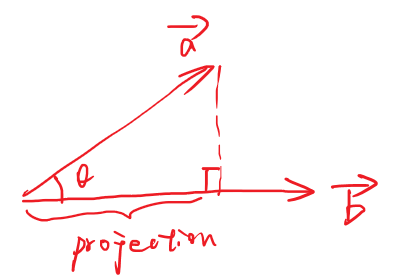
0. 预备知识 - 向量投影
向量投影:
![]()
1. 算法原理
- 将x向量往最大投影向量ukˉ处投影:
(xiT⋅uk)uk
-
令投影后向量的方差最大
J=N1⋅i=1∑N((xi−xˉ)⋅uk)2=N1⋅i=1∑N((xi−xˉ)⋅uk)T⋅((xi−xˉ)⋅uk)=i=1∑NN1ukT(xi−xˉ)(xi−xˉ)Tuk=ukT[i=1∑NN1(xi−xˉ)(xi−xˉ)T]uk=ukTSp×puk
条件:∣uk∣=1 ,也即ukT⋅uk=1
-
拉格朗日函数法,求上面的极大值:
L(uk,λ)=ukTSp×puk+λ⋅(1−ukT⋅uk)
求导后等于0:
∂uk∂L=2⋅Sp×p⋅uk−λ⋅2⋅u1=0
可得:
S⋅uk=λ⋅uk
综上可得,投影向量为方差矩阵Sp×p的特征向量。
![]()
2. 算法流程
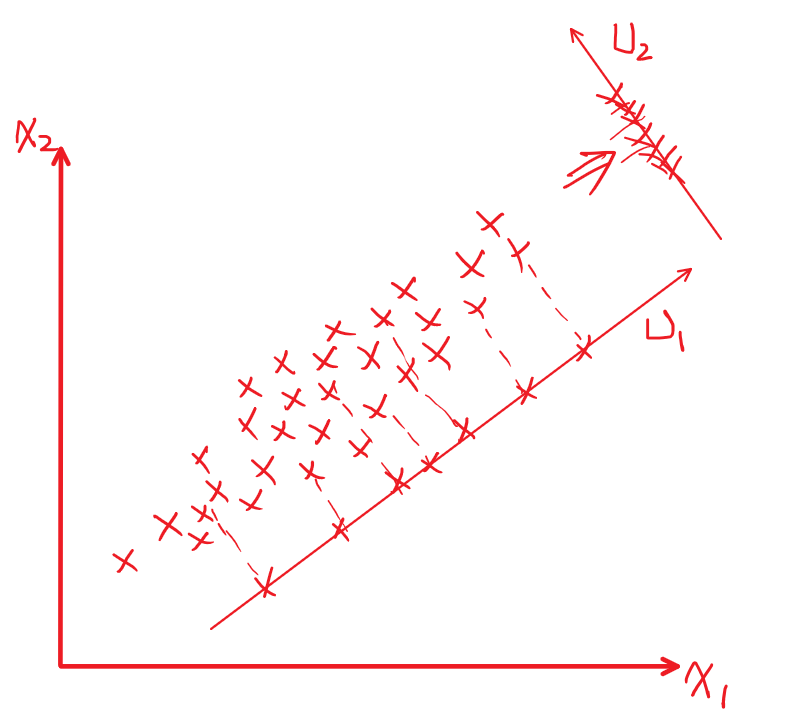
最小重构原理
-
降维的思路:
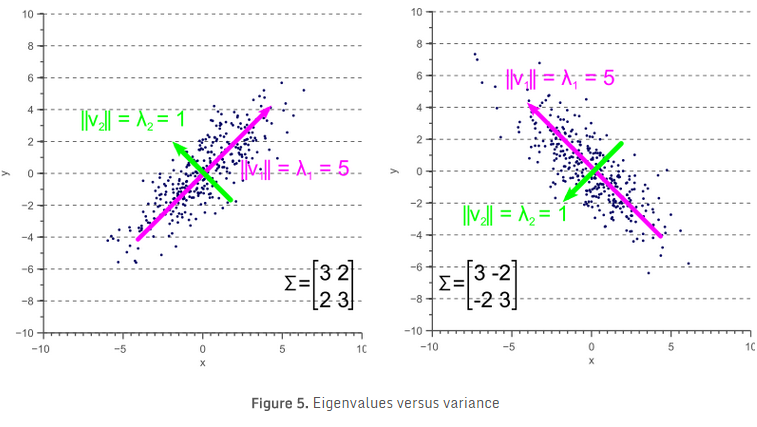
- 先利用方差矩阵Sp×p可以找到一组独立的基向量{u1,u2,…,up}对应的特征值为 {λ1,λ2,…,λp}
- 压缩降维,选择前q个最大值的λ
![]()
-
根据投影方向向量uk来重构原先的坐标xk
xi=k=1∑P(xiT⋅uk)⋅uk
x^=k=1∑q(xiT⋅uk)⋅uk
-
最小重构代价:
J=i=1∑NN1∥xi−xi^∥2=k=q+1∑pukTSuk
同理要求:ukT⋅uk=1
总结
最大投影方差等价于 最小重构原理
目的:从uk轴重构回去的损失最小
PCA 实践:
基础:SVD 奇异值分解
上述公式只有两个特征值,说明原向量的维度是2,方差矩阵是S2×2 ,降维的话,直接舍弃其中的一个部分即可。现在的问题就是如何求以上的几个值?
三种角度看PCA降维问题:
空间重构原理:
找到方差矩阵,进行特征值分解,对应的特征值向量,即为主方向【即可】
Sp×p=G⋅K⋅GTs.t.GTG=1
其中K值为:
K = ⎣⎢⎢⎡k1k2⋱kp⎦⎥⎥⎤k1≥k2≥k3≥⋯≥kp
-
如何还原?
-
选择前q个最大的K值,所对应的特征向量uk即可。
-
有了最大的投影向量,我们直接往最大方向投影就ok了!
无损失:
xi=k=1∑P(xiT⋅uk)⋅uk
少选几个特征:
x^=k=1∑q(xiT⋅uk)⋅uk
通过对中心化后的数据,求SVD奇异值分解,奇异值的平方即为特征值
这里直接对中心化后的数据进行SVD分解
HX=UΣVT=(λ1)u1(v1)T+(λ2)u2(v2)T+⋯
-
如何计算
- HX(HX)T 进行特征对角化处理 ,可以求得:λ、u
- (HX)THX 进行特征对角化处理,可以求得:λ、v
-
如何还原?
取前k项即可,取得越多越近似!
主坐标分析法(PCoA)
Principle coordinate analysis
背景说明:
若此时$S_{p \times p} $中维度P远远大于样本的个数 N 时,【如图片处理,维度都是几万维】求解Sp×p还是比较困难的。有没有解决简单的方法可以跳过对方差的计算?当然有!
-
前两个方法的缺点:
- 当$S_{p \times p} $的维度太大的时候,计算效率太低
注:SVD分解中,其实也蕴含着对方差的计算,如:对xTHTHx进行特征分解。
Sp×p=N1xTH⋅(xTH)T=N1xTHTHx
-
PCA中的结果:
第一步:我们在PCA中的目的,就是为了找到一组能使方差最大化的特征向量。
第二步:将中心化后的特征HX直接投到这组新的坐标下,即与特征向量v进行点积,在新坐标系vk下的坐标值 UΣ。公式如下:
HX⋅V=UΣVTV=UΣ
然后,,坐标值为UΣ。
-
若直接对 HX(HX)T 进行特征对角化处理 ,可以求得:Σ 和 U
将两者相乘,就直接得到了我们在新坐标系下的坐标。
![]()
PCA代码实践
A = ⎣⎢⎢⎢⎢⎡3245120003000500080002000⎦⎥⎥⎥⎥⎤
Python基础实现:
-
数据预处理,【数据归一化,数据缩放】
中心化公式:H⋅X
mean = np.mean(A, axis=0)
norm = A - mean
scope = np.max(norm, axis=0) - np.min(norm, axis=0)
norm = norm / scope
|
-
奇异值分解:
H⋅X=UΣVT=(λ1)u1(v1)T+(λ2)u2(v2)T
U, S, V = np.linalg.svd(np.dot(norm.T, norm))
U
array([[-0.67710949, -0.73588229],
[-0.73588229, 0.67710949]])
|
-
选取特征矩阵的第一个列来构造
R^=(λ1)u1(v1)T
U_reduce = U[:, 0].reshape(2,1)
R = np.dot(norm, U_reduce)
R
array([[ 0.2452941 ],
[ 0.29192442],
[-0.29192442],
[-0.82914294],
[ 0.58384884]])
|
-
还原:
投影公式:
Z=HX⋅V
说明:V是一个正交矩阵,有:V⋅VT=V⋅V−1=E
还原公式:
H⋅X=Z⋅V−1=Z⋅VT
Z = np.dot(R, U_reduce.T)
Z
array([[-0.16609096, -0.18050758],
[-0.19766479, -0.21482201],
[ 0.19766479, 0.21482201],
[ 0.56142055, 0.6101516 ],
[-0.39532959, -0.42964402]])
|
-
反中心化和反数据放缩
np.multiply(Z, scope) + mean
|
sklearn调包:PCA
![]()
![]()