LogisticRegression参数说明

from sklearn.linear_model import LogisticRegression

直接拷贝博文： https://www.cnblogs.com/wjq-Law/p/9799220.html

LogisticRegression(penalty='l2', dual=False, 
    tol=0.0001, C=1.0, fit_intercept=True, 
    intercept_scaling=1, class_weight=None, 
    random_state=None, solver='warn', max_iter=100,
    multi_class='warn', verbose=0, 
    warm_start=False, n_jobs=None)

• penalty：惩罚项，可为'l1' or 'l2'。'netton-cg', 'sag', 'lbfgs'只支持'l2'。

1. 'l1'正则化的损失函数不是连续可导的，而'netton-cg', 'sag', 'lbfgs'这三种算法需要损失函数的一阶或二阶连续可导。
2. 调参时如果主要是为了解决过拟合，选择'l2'正则化就够了。若选择'l2'正则化还是过拟合，可考虑'l1'正则化。
3. 若模型特征非常多，希望一些不重要的特征系数归零，从而让模型系数化的话，可使用'l1'正则化。

• dual：选择目标函数为原始形式还是对偶形式。

将原始函数等价转化为一个新函数，该新函数称为对偶函数。对偶函数比原始函数更易于优化。

• tol：优化算法停止的条件。当迭代前后的函数差值小于等于tol时就停止。
• C：正则化系数。其越小，正则化越强。
• fit_intercept：选择逻辑回归模型中是否会有常数项b【一般默认都是默认有的】。
• intercept_scaling：
• class_weight：用于标示分类模型中各种类型的权重，{class_label: weight} or 'balanced'。

比如对于0,1的二元模型，我们可以定义class_weight={0:0.9,1:0.1}，这样类型0的权重为90%，而类型1的权重为10%。

分类中存在的两类问题：

• 误分类的代价很高，将非法用户分类为合法用户的代价很高，我们宁愿将合法用户分类为非法用户，这时可以人工再甄别，但是却不愿将非法用户分类为合法用户。这时，我们可以适当提高非法用户的权重。
• 样本是高度失衡的：如二元样本数据10000条，里面合法用户有9995条，非法用户只有5条

调节样本权重的方法有两种

• 在class_weight使用balanced。某种类型样本量越多，则权重越低，样本量越少，则权重越高,会自动计算对应的权重，计算公式为：

  $\frac{n_{samples}}{n_{classes}\cdot (np.bincount(y))}$

• 在调用.fit函数时，通过sample_weight来自己调节每个样本权重。在scikit-learn做逻辑回归时，如果上面两种方法都用到了，那么样本的真正权重是class_weight*sample_weight。

• random_state：随机数种子。

• solver：逻辑回归损失函数的优化方法。

1. 'liblinear'：使用了开源的liblinear库实现，内部使用了坐标轴下降法来迭代优化损失函数。liblinear是一个针对线性分类场景而设计的工具包，支持线性的SVM和Logistic回归等，但是无法通过定义核函数的方式实现非线性分类。

   备注：libSVM是一套完整的SVM模型实现。用户可以在libSVM中使用核函数来训练非线性的分类器，当然也能使用更基础的线性SVM。由于支持核函数的扩展，libSVM理论上具有比liblinear更强的分类能力，能够处理更为复杂的问题。但是针对线性分类，liblinear无论是在训练上还是在预测上，都比libSVM高效得多。此外，受限于算法，libSVM往往在样本量过万之后速度就比较慢了，如果样本量再上升一个数量级，那么通常的机器已经无法处理了。但使用liblinear，则完全不需要有这方面的担忧，即便百万千万级别的数据，liblinear也可以轻松搞定，因为liblinear本身就是为了解决较大规模样本的模型训练而设计的。关于libSVM和liblinear两者差异，不妨看看LIBSVM与LIBLINEAR

2. 'lbfgs'：拟牛顿法的一种。利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

3. 'newton-cg'：也是牛顿法家族的一种，利用损失函数二阶导数矩阵即海森矩阵来迭代优化损失函数。

4. 'sag'：随机平均梯度下降。每次迭代仅仅用一部分的样本来计算梯度，适合于样本数据多的时候。

5. 多元逻辑回归有OvR(one-vs-rest)和MvM(many-vs-many)两种，而MvM一般比OvR分类相对准确一些。但是，'liblinear'只支持OvR。

• max_iter：优化算法的迭代次数。

• multi_class：'ovr' or 'multinomial'。'multinomial'即为MvM。

1. 若是二元逻辑回归，二者区别不大。
2. 对于MvM，若模型有T类，每次在所有的T类样本里面选择两类样本出来，把所有输出为该两类的样本放在一起，进行二元回归，得到模型参数，一共需要T(T-1)/2次分类。

• verbose：控制是否print训练过程。
• warm_start： 是否使用之前的解决方法作为初始拟合。
• n_jobs：用cpu的几个核来跑程序。-1自动选择CPU的合数，1：默认值

LogisticRegressionCV参数说明

from sklearn.linear_model import LogisticRegressionCV

• 相比于LogisticRegression，LogisticRegressionCV使用交叉验证来选择正则化系数C。

参考论文：

• https://www.jianshu.com/p/bbdeb356057e

• https://blog.csdn.net/weixin_41712499/article/details/82526483

l1和l2范数正则化：

• L1：

$\min _{w, c}\|w\|_{1}+C \sum_{i=1}^{n} \log \left(\exp \left(-y_{i}\left(X_{i}^{T} w+c\right)\right)+1\right)$

• L2：

$\min _{w, c} \frac{1}{2} w^{T} w+C \sum_{i=1}^{n} \log \left(\exp \left(-y_{i}\left(X_{i}^{T} w+c\right)\right)+1\right)$

Solver使用技巧

• newton-cg, bfgs和sag这三种优化算法时都需要损失函数的一阶或者二阶连续导数，因此不能用于没有连续导数的L1正则化，只能用于L2正则化。而liblinear通吃L1正则化和L2正则化。

• sag每次仅仅使用了部分样本进行梯度迭代，所以当样本量少的时候不要选择它，而如果样本量非常大，比如大于10万，sag是第一选择。但是sag不能用于L1正则化，所以当你有大量的样本，又需要L1正则化的话就要自己做取舍了。要么通过对样本采样来降低样本量，要么回到L2正则化。

• 从上面的描述，大家可能觉得，既然newton-cg, lbfgs和sag这么多限制，如果不是大样本，我们选择liblinear不就行了嘛！错，因为liblinear也有自己的弱点！我们知道，逻辑回归有二元逻辑回归和多元逻辑回归。对于多元逻辑回归常见的有one-vs-rest(OvR)和many-vs-many(MvM)两种。而MvM一般比OvR分类相对准确一些。郁闷的是liblinear只支持OvR，不支持MvM**，这样如果我们需要相对精确的多元逻辑回归时，就不能选择liblinear了。**也意味着如果我们需要相对精确的多元逻辑回归不能使用L1正则化了。

• 总结

  可用范数	算法	说明
  	liblinear	*iblinear**适用于小数据集；如果选择L2正则化发现还是过拟合，即预测效果差的时候，就可以考虑L1正则化；*如果模型的特征非常多，希望一些不重要的特征系数归零，从而让模型系数稀疏化的话，也可以使用L1正则化。
  L2	liblinear	ibniear只支持多元逻辑回归的OvR，不支持MvM，但MVM相对精确。
  L2	lbfgs/newton-cg/sag	较大数据集，支持one-vs-rest(OvR)和many-vs-many(MvM)两种多元逻辑回归。
  L2	sag	如果样本量非常大，比如大于10万，sag是第一选择*；但不能用于L1正则化。*

Solver算法的详解：

• 牛顿法求根：

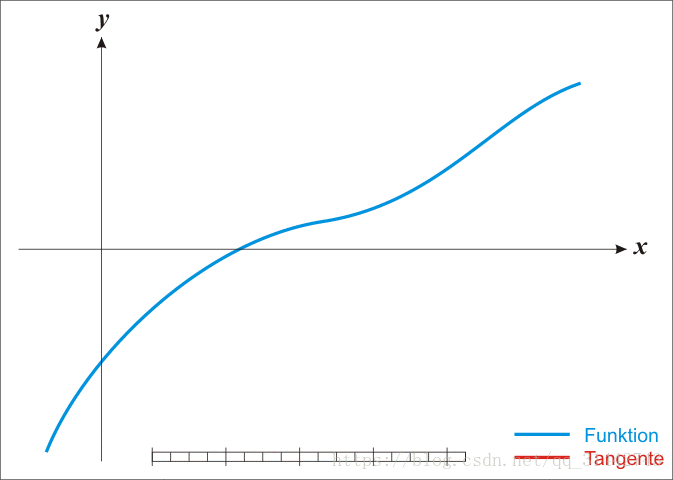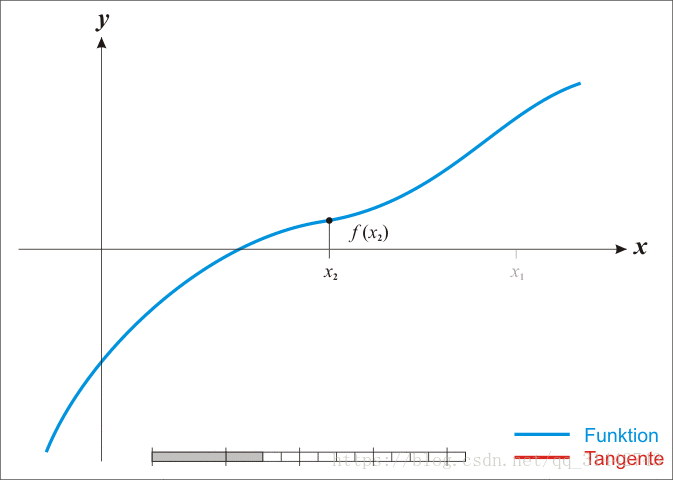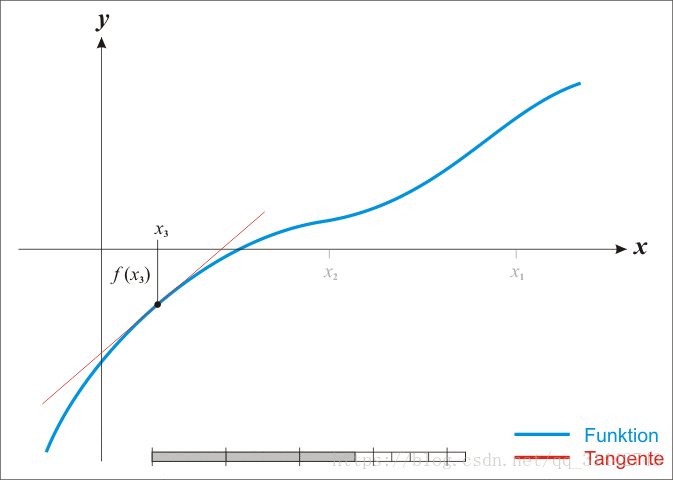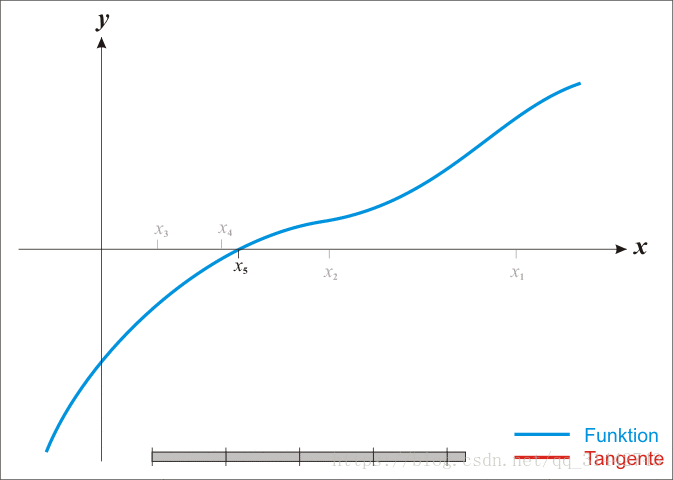
推导迭代公式：

$x_{k}=x_{k-1}-\frac{f\left(x_{k-1}\right)}{f^{\prime}\left(x_{k-1}\right)}$

$x_1$是随机出来的已知值，$x_2,x_3,\dots,x_k$由上面的迭代公式计算得出。

• 牛顿法求函数的驻点

机器学习中将导函数等于零的点作为机器学习算法表现最好的点。利用牛顿法可以求导函数等于零的根，即函数的驻点。

故将上述的 $f$ 全部换做 $f^{\prime }$,可得：

$x_{k}=x_{k-1}-\frac{f^{\prime}\left(x_{k-1}\right)}{f^{\prime \prime}\left(x_{k-1}\right)}$

此时x是一个向量，$f^{\prime }(x)$也是一个向量，对$f^{\prime }(x)$求导后的$f^{\prime \prime}(x)$是Hessian矩阵，上式公式等价为：

$\mathbf{x}_{k+1}=\mathbf{x}_{k}-H_{k}^{-1} \cdot \mathbf{g}_{k}, \quad k=0,1, \cdots$

其中：$H_k^{-1}$是二阶导函数的倒数，$g_k$就是$f^{\prime}(x_k)$

当$x$的维度特别多的时候,我们想求得$f^{\prime \prime}$是非常困难的.而牛顿法求驻点又是一个迭代算法,所以这个困难我们还要面临无限多次,导致了牛顿法求驻点在机器学习中几乎无法使用。

• 通过BFGS算法来逼近$H_k^{-1}$

  $D_{k+1}=\left(I-\frac{s_{k} y_{k}^{T}}{y_{k}^{T} s_{k}}\right) D_{k}\left(I-\frac{y_{k} \cdot r_{k}^{T}}{y_{k}^{T} s_{k}}\right)+\frac{s_{k} \cdot r_{k}^{T}}{y_{k}^{T} s_{k}}$

  其中$D_k$就是$H_k^{-1}$。$s_k=x_{k+1}-x_k$,$y_k=g_{k+1}-g_{k}$。$g_k$ 就是原函数的导数。

• 总计流程：

  • $D_1$是单位矩阵$I$
  • 牛顿法求驻点算法的第一步是：$x_2=x_1-I^{-1}\cdot f^{\prime}(x_1)$
  • 再通过BFGS算法去更新$H_k^{-1}$
  • 通过牛顿法求驻点的第二步：$x_3=x_2-H_2^{-1}\cdot f^{\prime}(x_2)$

  所以BFGS算法可以理解为从梯度下降逐步转换为牛顿法求函数解的一个算法。

• L-BFGS算法:

  $D$ 矩阵有多大呢.假设我们的数据集有十万个维度(不算特别大),那么每次迭代所要存储 $D$ 矩阵的结果是74.5GB。

  我们每一次对D矩阵的迭代,都是通过迭代计算和得到的.既然存不下D矩阵,那么我们存储下所有的和,想要得到就用单位矩阵同存储下的和到和计算就可以了。这样一个时间换空间的办法可以让我们在数据集有10000个维度的情况下,由存储10000 x 10000的矩阵变为了存储十个1 x 10000的10个向量,有效节省了内存空间。

  但是,仅仅是这样还是不够的,因为当迭代次数非常大的时候,我们的内存同样存不下.这个时候只能丢掉一些存不下的数据.假设我们设置的存储向量数为100,当s和y迭代超过100时,就会扔掉第一个s和y,存储到和到,每多一次迭代就对应的扔掉最前边的s和y.这样虽然损失了精度,但确可以保证使用有限的内存将函数的解通过BFGS算法求得到。

  所以L-BFGS算法可以理解为对BFGS算法的又一次近似