这部分内容自己掌握的也不是很好,但是先做个学习笔记把,以后有错误再回过头来改。本篇学习笔记基于邹博,白板推导,西瓜书,深度之眼解析课,统计机器学习等内容。按说讲课的话这部分课的内容还是很简单的。
第一部分:贝叶斯决策论
想来想去还是按照白板书的板书风格理清思路吧。
变量记号声明:
-
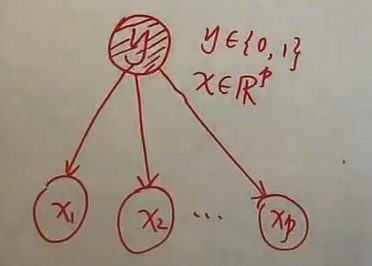
存在K中可能分类,即输出特征类别标记y∈Y={c1,c2,…,cK},输入特征向量X=(x(1),x(2),…,x(p))∈X⊆Rn。需要注意的是这里X,Y都是随机变量。故可以求两个随机变量的联合概率分布P(X,Y)。这里用上标加括号代表各个属性。设有n个属性
-
训练数据集
T={(x1,y1),(x2,y2),…,(xN,yN)}
严格来讲:还需加上P(X,y)是独立同分布的。
-
需要指出的是,也是我一直理解的难点:P(xi∣yi)不是条件假设,因为xi,yi的取值是确定的,因为他们都是训练数据集,属于已知量。而P(X,y)中的变量都是随机变量。
寻找总体风险
-
从最朴素的想法入手,计数。当预测类别和原样本标签相同的时候,不计数,当预测类别和标签不同,则预测错误,统计所有样本下的作为损失函数。
L(y,f(X))={1,0,y=f(X)y=f(X)
注:这里的f(X)就是我们要训练出的模型。【即,判定准则:X:Rp↦Y:R1】
-
我的理解:如果像之前那的优化类模型构造损失函数的做法,就是把所有样本下的损失函数统计出来类似与正则化项∑i=1Nmax{0,1−yi(wiT+b)},而贝叶斯分类器从学派上属于贝叶斯学派,它认为待预测的结果也是具有分布的。这点其实很奇怪比如说预测瓜是好是坏,但是贝叶斯公式中避不开求先验概率p(c),而这部分完全是由训练样本取决的即,先验分布。
-
利用期望求风险函数
R(f)=Ep(x,y)[L(y,f(X))]
这里X是连续随机变量【或离散】,y是离散随机变量。把联合改为条件p(X,y)=p(y∣X)⋅p(X)
R(f)=EX[k=1∑KL(y=ck,f(X))⋅P(y=ck∣X)]
逐个对X=x进行极小化:
f(x)====argy∈Ymink=1∑KL(y=ck,f(X))⋅P(y=ck∣X=x)argy∈Ymink=1∑KP(y=ck∣X=x)argy∈Ymin(1−P(y=ck∣X=x))argy∈YmaxP(y=ck∣X=x)
注:这里X=x代表:X(1)=x(1),⋯,X(n)=x(n),x是实数。
组合爆炸
现需求联合概率分布P(X,y)的参数,计算上组合爆炸【组数级数量】,在数据上将会遭遇样本稀疏;属性越多,问题越严重。
若实数x(j)可取值Sj个,j=1,2,…,p,而Y集合中可取值K个,参数个数为:K∏j=1pSj
举例如下:
| x1 |
x2 |
c |
| a |
d |
1 |
| b |
e |
2 |
| c |
f |
3 |
- 组合爆炸:(x1,x2,c)之间的组合:3×3×3=27
- 特征独立:(x1,c)的组合,(x2,c)的组合:3×3+3×3=18
第二部分:朴素贝叶斯分类器
本质:“属性条件独立性假设”,目的:牺牲一定的准确率,换取计算量的骤减。
P(c∣X)=P(X)P(c)P(X∣c)=P(X)P(c)i=1∏pP(X(i)∣c)∝P(c)i=1∏pP(X(i)∣c)
-
P(c)是先验分布,可以通过频率来进行估计【即为一次多项式分布】
P(c)=∣D∣∣Dc∣
-
注意到这里的P(X(i)∣c)属于似然概率
-
离散取值:
P(X(i)∣c)=∣Dc∣∣Dc,xi∣
-
连续属性:
P(X(i)∣c)=(wπ)1σc,iexp(−2σc,i2(X(i)−μc,i)2)
具体案例举例:
| 编号 |
色泽 |
根蒂 |
敲声 |
纹理 |
脐部 |
触感 |
密度 |
含糖率 |
好瓜 |
| 测1 |
青绿 |
蜷缩 |
浊响 |
清晰 |
凹陷 |
硬滑 |
0.697 |
0.460 |
? |
第一步:先验分布P(c)
P(c=1)=178≈0.471P(c=0)=179≈0.529
第二步:条件概率P(X(i)∣c):
X(1)是色泽;X(2)是根蒂;X(3)是敲声;X(4)是纹理;X(5)是脐部;X(6)是触感;X(7)是密度;X(8)是含糖率。
第三步:判断准则 P(c∣X=(X(1),X(2),…,,X(8)))
选择:P(c=1∣X=(X(1),X(2),…,,X(8)))和P(c=0∣X=(X(1),X(2),…,,X(8)))的概率大的类别作为判断类别。
各种分布的概念
-
伯努利分布X∼B(1,p):求抛一次硬币,预测结果为正面的次数为1的概率为
P(X=0)=P(X=1)=1−pp
-
二项分布 X∼B(n,p): 求多次抛硬币,预测结果为正面的次数为k的概率为
P(X=k)=Cnkpk(1−p)n−k,k=0,1,2,…,n
-
多项式分布X∼C(n,p):求多次抛色子,预测结果为第一面的次数为n1次,第二面的次数为n2次,…,第六面的次数为n6次的联合概率为:。
设总共抛n次。故:∑i=1kni=n
P(X1=n1,X2=n2,…,X6=n6)=n!i=1∏kni!pini
朴素贝叶斯的问题
在西瓜书第一节,对于如何求类条件概率P(X∣c),不能用样本出现的频率去求解。但是在这一节中用的就是频率去求取的这个值。
频率为0的含义:“未被观测到”与“出现概率为零”。
问题:若是测试样本中,出现了一个新的属性如**“敲声=清脆”**,但是P(”敲声=清脆“|好瓜)=P(”敲声=清脆“|坏瓜)=0
“拉普拉斯修正”:
P^(c)=∣D∣+N∣Dc∣+1P^(xi∣c)=∣Dc∣+Ni∣Dc,xi+1∣
当训练样本中若存在这个属性【即,正常状态】因为样本类别一般是很小的N,而样本∣Dc∣还是很大的。所以修正后P^(c)≈P(c)。
第三部分:频率派与贝叶斯派的浅见
在小节1.2中,我们利用期望去寻求总体风险,与求SVM正则项相同的是,对分类错误的个数进行计数作为损失函数。但是贝叶斯分类器却是通过概率的角度去分析问题。因为X是随机变量,y也是随机变量,故可以通过计算联合概率P(X,y)去计算损失的期望【即,均值】。两者不同之处在于,前者让损失最小,即让分类正确的样本出现的概率最大。后者考虑到了先验分布,即好瓜与坏瓜的比例。在前者的基础上再乘上一个先验P(c)【为了变成概率,所以进行归一化(除以P(x))】。
![]()
频率派:θ是一个未知的常量
优化手段:MLE(极大似然估计)
步骤:
- 构造概率模型P(x;ω)
- 设置Loss function
- max(LL(θ))
贝叶斯学派:θ也是一个分布
优化手段:MAP(最大后验概率问题)
本质: 求积分问题(积分比较难求可以用MCMC蒙特卡洛方法)
区别:
-
频率派:maxP(x;θ)) ,即为似然函数
-
贝叶斯派:maxP(θ∣x)∝maxP(x∣θ)P(θ) 相当于似然函数乘上先验概率再做归一化
形象化说明:
如掷色子,我们想知道每个面的概率是多少?上帝视角中我们已知:真值是1/6。频率派的解决方法:就是根据多次投掷直接计算每个面超上的频率,当样本量足够大时,根据大数定理,频率就变成概率了。而贝叶斯学派的手段是,利用一部分先验知识,如已知每个面重量相同,估计是1/6,当它扔了五次都是1超上,那我会对它的先验产生质疑并修正,假设认为1朝上的概率为:1/2。若色子是均匀的,这个结果肯定是可笑的。但是大部分情况下我们并不知道我们结果的真值是多少?所以若站在普通人的角度去看这个结果是可接受的。最终随着样本量的增加,均值会逐渐趋于期望【期望就是站在上帝视角,与样本无关】
解释期望为什么是上帝视角:若计算掷色子的期望,E(X)=61⋅1+⋯+61⋅6=3
此时根据样本可以计算出样本均值:假设为3.5。差别在哪儿?因为我们在上帝视角中已经知道了61就是每个面朝上的概率。但是实际的样本值可能是2,2,1,3,2,5,6,7,8等。明显2出现的频率高,但是此时频率不等同于概率P(x=2),根据大数定律,样本量趋于无穷才是概率。逻辑是:当样本量越大,频率越趋于概率,则由频率计算出的均值也就越接近于期望【即,所谓的上帝视角】