本篇内容基于西瓜书与邹博视频总结而成
第一部分:有关信息论以及熵的构造
主要知识点:
我的理解:熵等价于不确定度
熵的构造:
- 基本想法:当一个不可能发生的事情发生了,包含的信息的不确定性大
太阳东升西落:这件事情不携带任何不确定性,而地震发生的不确定性还是有的,我们的目标就是找到事情发生的不确定性,并且使它发生的概率最小。
- 构造:首先希望满足概率可加性:加对数 (经典底为2,不过底数对于模型极值无意义) ,其次:概率越小⇒ 不确定信息越多⇒ 添负号
即:p 【事件发生的概率)】 | 度量:−ln(p)
熵:所有随机事件不确定度的综合,即求事件的期望
i=1∑Np(i)⋅lnp(i)
条件熵 H(Y|X)
条件熵的定义是:是在X已经发生的情况后,Y发生“新”的不确定度(熵)
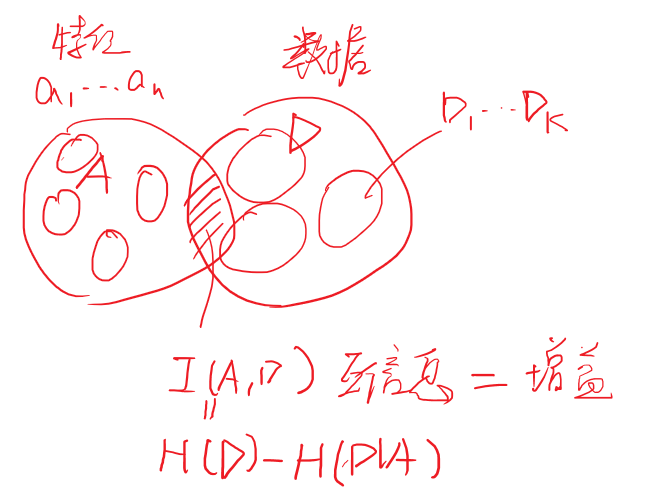
根据上述定义可有:H(X,Y)−H(X)
【X,Y所有包含的不确定度 】 减去 【X所含的不确定度 】 等于 【在X的基础上的额外的不确定度】
如果画出文氏图就能更好的理解:
![]()
推导条件熵的具体表达式:
H(X,Y)−H(X)=====−x,y∑p(x,y)logp(x,y)+x∑p(x)logp(x)−x,y∑p(x,y)logp(x,y)+x∑(y∑p(x,y))logp(x)−x,y∑p(x,y)logp(x,y)+x,y∑p(x,y)logp(x)−x,y∑p(x,y)logp(x)p(x,y)−x,y∑p(x,y)logp(y∣x)
可以发现上面最后这个式子不是很友好,前面是联合概率,后面是条件概率,将上面的联合概率变为条件概率看你那个得到什么结果?
H(X,Y)−H(X)======−x,y∑p(x,y)logp(y∣x)−x∑y∑p(x,y)logp(y∣x)−x∑y∑p(x,y)logp(y∣x)−x∑p(x)p(y∣x)logp(y∣x)x∑p(x)(−y∑p(y∣x)logp(y∣x))x∑p(x)H(Y∣X=x)
上述公式得到的是条件熵的表达式,在之后计算互信息时需要用到。
在决策树中,X代表文氏图中的A=(a1,a2,…,aV),即评价西瓜可以从V个特征入手,如瓜的颜色,瓜的大小。而Y则是文氏图中的D,可以用来表示分类的结果。具体的来讲假设Y=1表示瓜熟,Y=−1表示瓜生。
⭐️始终记住:熵的公式是根据真实类别计算的“纯度或不确定度”
Ent(D)=−k=1∑Kpkln(pk)
当我们引入不同的特征属性划分瓜后,即在每个特征子类【如:某一集合中瓜的颜色全是绿色,在此集合中仍有好瓜坏瓜之分】中,可以根据真实的target再进行一次熵的计算,这部分就是上式中的H(Y∣X=x)。
而这样计算结束了吗?肯定没有,问题在于特征子集合中的样本个数是不一致的,但是计算出的熵值量级是差不多的。如根据瓜的颜色划分后的集合中有50个样例,计算出熵值0.6,而根据瓜的纹理划分后的集合中只有5个样例,同样计算出熵值0.6。所有当我们有K个特征划分依据时,可以计算得到K个熵值。此时不能简单的把这些熵值加和取平均,因为明显大样本下的熵值计算才比较靠谱。故根据样本个数对K个熵值进行加权处理才是合理的。这步就是上式中的p(x)的作用。
信息增益:加入特征前后的熵的变化
根据定义:Ent(D)−Ent(D∣A)
Ent(D)−Ent(D∣A)=Ent(D)−v=1∑V∣D∣∣Dv∣Ent(Dv)
这个等号在概念上很好理解,我们根据加入A后计算各个子节点的熵,因为每个子节点划分后样本数量不相同,所以要对这些熵进行加权处理。下面是西瓜书的数学表达公式,同邹博表达式一样,只不过这里将数据都进行了离散化处理。西瓜书对连续值的离散化处理,请点击这里
Ent(D∣A)====−v,k∑p(Dv,Ai)logp(Dv∣Ai)−v,k∑p(Av)p(Dk∣Av)logp(Dk∣Av)−v=1∑Vk=1∑Kp(Av)p(Dk∣Av)logp(Dk∣Av)−v=1∑V∣D∣∣Dv∣k=1∑K∣Dv∣∣Dvk∣log∣Dv∣∣Dvk∣=−v=1∑V∣D∣∣Dv∣Ent(Dv)
这里的公式比较复杂,在西瓜书中Dv 说明一开这个数据集是由特征A 进行划分,但是这又是熵的计算,熵是根据样本分类K计算的不确定度。所以这里数据集Dvk 是先对A进行划分,之后再在DV的基础上对分类K进行划分。
第二部分 决策树生成策略
决策树采用的是自顶而下的递归方法,其基本思想是以信息熵为度量,选择熵值下降最快【信息增益最大】的属性作为第一个结点,之后的特征依次以此为标准生成决策树。终止条件:到叶子结点处的熵值为0,此时每个叶节点中的实例属于同一类。
如下图分析:
![]()
之前我们以信息熵作为度量,以信息增益作维选择特征的决策依据,其实还有其他的依据:
常用三种算法:
- ID3:信息增益(已学)
- C4.5:信息增益率(本节内容)
- CART:Gini系数(本节内容)
信息增益率
信息增益有个缺点。假设西瓜分为两类,好瓜和坏瓜。50个样本,其中一特征有100个属性。若用此属性作为划分依据,划分后每个类别的熵都为0【因为每个类别的瓜都可以被分到一节点,还记得怎么计算增益率吗?是先用V进行划分,再用K进行划分。这里V划分结束后,K已经不用划分了,因为只可能是一种类别】
属性a的固有值:
IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
a越大⇒ Dv 越均匀 ⇒ 熵值越大
信息增益率:
Gain ratio (D,a)=IV(a)Gain(D,a)
基尼系数 Gini
基尼数据定义:随机抽取两个样本,类别不一样的概率。
Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=1−k=1∑∣Y∣pk2
基尼指数【对照于增益】:
Gini index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
最优划分属性:
a∗=a∈AargminGiniindex(D,a)
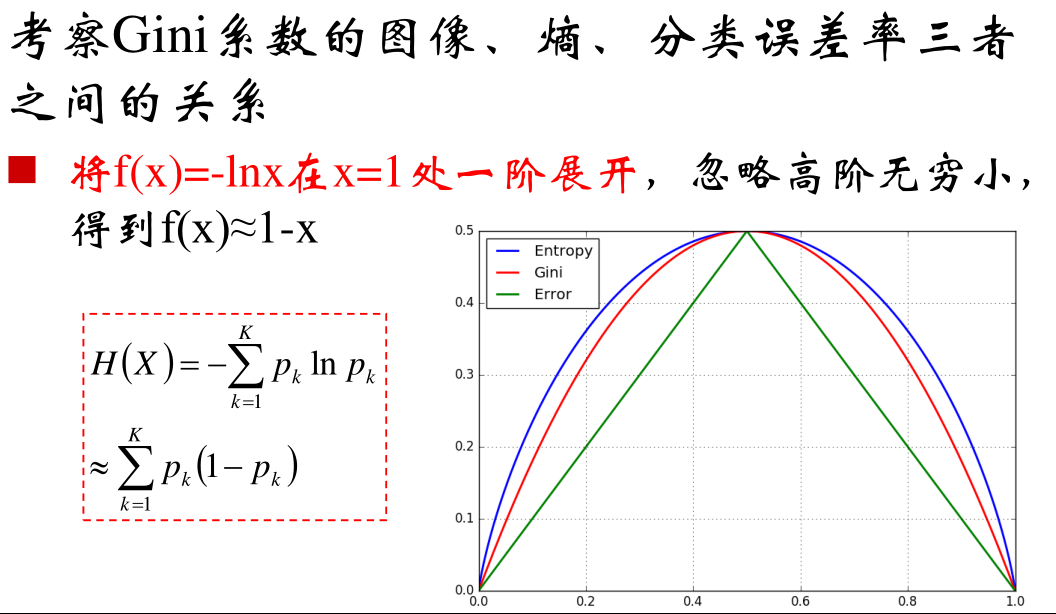
高阶认识: Gini系数就是信息熵的一阶泰勒近似
![]()
第三部分 算法调参
过拟合处理:
-
剪枝
-
随机深林
剪枝
西瓜书和邹博讲的剪枝手段不一样啊。
⭕️【邹博思路】:
-
决策树的评价
纯结点的熵为:Hp=0 ,最小
均结点的熵为:Hu=lnk ,最大
对所有叶节点的熵进行求和,值越小,说明样本的分类越精细。
考虑到每个结点的样本数目是不一样的,所以评价函数采用样本加权求熵和
评价函数:
C(T)=t∈leaf∑Nt⋅H(t)
将此作为损失函数。
-
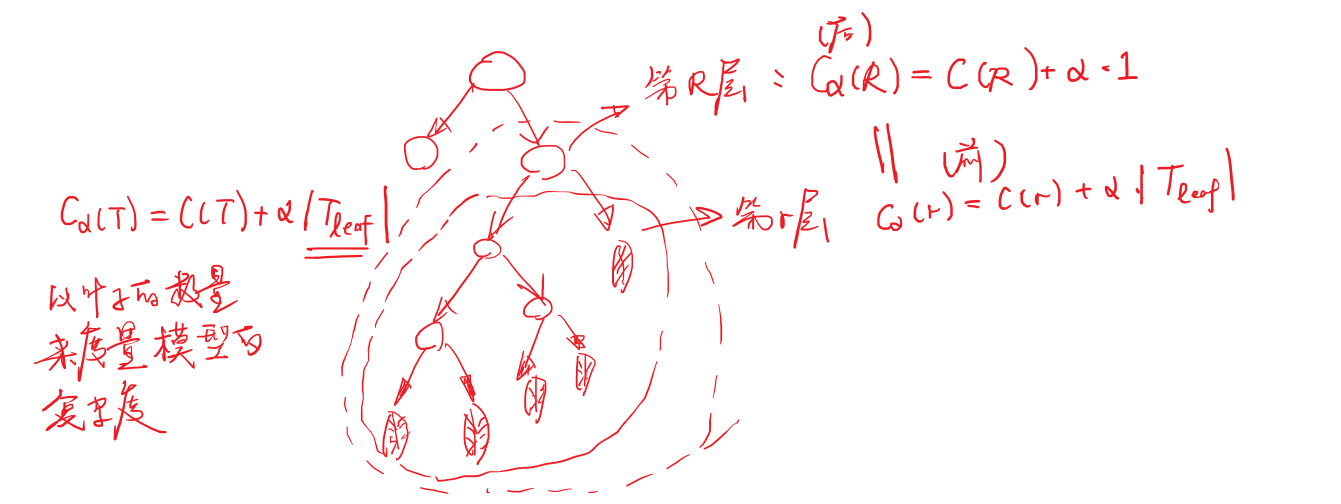
正则化考虑:以叶子的数目作为复杂度
损失函数:
Cα=C(T)+α∣Tleaf∣
![]()
目标:求在保证损失不变的情况下,模型的复杂度是多少?(剪枝系数)
α=<Rleaf>−1C(r)−C(R)
⭐️剪枝算法:
- 对于给定的决策树T:
- 计算所有内部节点的剪枝系数;
- 查找最小剪枝系数的结点,剪枝得决策树Tk;
- 重复以上步骤,直到决策树T,只有1个结点;
- 得到决策树序到 T0T1T2…Tk;
- 使用验证样本集选择最优子树。
注:当用验证集做最优子树的标准,直接用之前不带正则项的评价函数:C(T)=∑t∈leafNt⋅H(t)
⭕️【西瓜书】
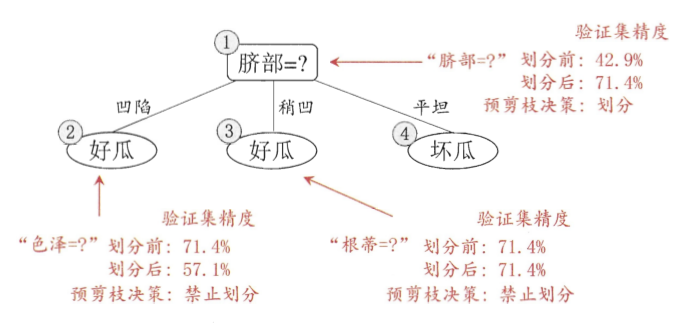
西瓜书的剪枝手段主要是通过验证集去选择,并且把剪枝分为预剪枝和后剪枝
![]()
![]()
注:预剪枝基于的是贪心算法,只要验证集精度提高了,我就剪枝,所以有欠拟合的风险。而后剪枝是自底向上对所有非叶结点进行逐一考察,时间开销大的多,但是泛化能力提高。
连续值和缺失值处理
⭕️连续值处理:
给定样本集D和连续属性a,假定a在D上出现了n个不同的取值,将这些值从小到大进行排序,记为{al,a2..,an}.基于划分点t可将D分为子集Dt−和Dt+,其中Dt−包含那些在属性a上取值不大于t的样本,而D则包含那些在属性a上取值大于t的样本。我们可考察包含 n−1 个元素的候选划分点集合:
Ta={2ai+ai+1∣1⩽i⩽n−1}
缕一缕:一个结点有n−1个候选划分点:
综上公式改为:
Gain(D,a)=t∈TamaxGain(D,a,t)=t∈TamaxEnt(D)−λ∈{−,+}∑∣D∣∣∣Dtλ∣∣Ent(Dtλ)
⭕️缺省值:
我们需解决两个问题:(1)如何在属性值缺失的情况下进行划分属性选择?(2)给定划分属性,若样本在该属性上的值缺失,如何对样本进行划分?
无缺失值样本所占的比例:
ρ=∑x∈Dwx∑x∈D~wx
无样本下第k类的比例和第v个属性的比例:【与之前的公式相同】
p~kr~v=∑x∈D~wx∑x∈D~kwx(1⩽k⩽∣Y∣)=∑x∈D~wx∑x∈D~vwx(1⩽v⩽V)
wx是每个样本x的权重,根结点中的样本权重为1。
增益公式推广为:
Gain(D,a)=ρ×Gain(D~,a)=ρ×(Ent(D~)−v=1∑Vr~vEnt(D~v))
多变量决策树
⭕️同一个特征可以进行多次判别:
![]()
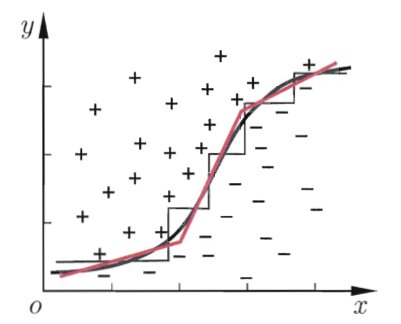
⭕️一般而言,分类边界为:轴平行(axis-parallel),但是也可以将线性分类器作为决策标准,可以产生"斜"这的分类边界。
![]()
技巧:可利用斜着的分裂边界简化决策树模型
![]()