本文的主要知识点：第一部分讲对Logistics的概念理解。第二部分讲公式推导，主要从两个角度去思考，其一、从广义线性模型的角度出发推导公式，另一点从伯努利分布推导。

第一部分对Logistics的概念理解

线性回归的非线性映射

早就听说过Logistics回归做的是分类的活，而非字面意思上的回归，那它和回归有什么关系呢？

在上一篇的线性回归模型中已经讲过一个观点，为什么线性回归是属性特征的线性组合呢？

其一是 $\omega$ 能够直观的显示出各个属性的权重大小，
其二就是模型足够简单，可以在线性回归模型的基础上增加高维映射变为非线性模型。

如：

$y = w^Tx+b$

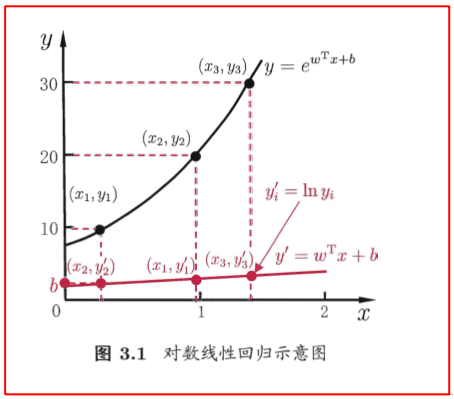
若预测值非线性变换，而是指数变换，换句话说就是预测值的对数是线性变换，如下：

$lny = w^Tx+b$

下图可以看作线性预测值 $y'$ 进行非线性 $y$ 的映射：

$y_i=e^{y_i'}=ln^{-1}(y_i')$

上述映射是“广义线性模型”的特殊形式：

$y = g^{-1}(w^Tx+b)$

$g(\cdot)$ 是联系函数，要求连续且充分光滑，上例是 $g(\cdot)=ln(\cdot)$ 的特例。

Logistics的核心是分类，但为啥叫回归？

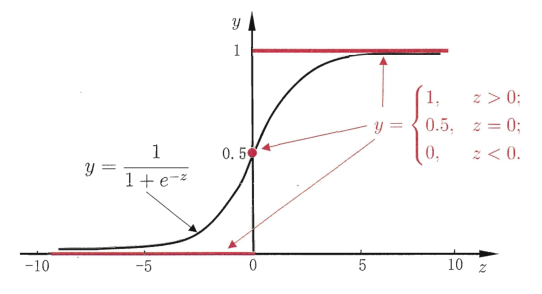
若是要做二分类：最简单的方式是阶跃函数

$y=\left\{\begin{array}{cc}{0,} & {w^Tx+b<0} \\ {0.5,} & {w^Tx+b=0} \\ {1,} & {w^Tx+b>0}\end{array}\right.$

但是阶跃函数有个致命的缺点：不可导。尤其在深度学习中，反向传播过程中需要对函数进行反向求导。所以提出了一个替代函数对数几率（odd）函数（logistic function）：

$y = \frac{1}{1+e^{-z}}=\frac{1}{1+e^{-(w^Tx+b)}}$

上述函数也称为 $sigmoid$ 函数：

将 $sigmoid$ 函数进行某种转换，结合第一节内容对比：

$\ln \frac{y}{1-y}=\boldsymbol{w}^{\mathrm{T}} \boldsymbol{x}+b$

这个公式解释了为啥叫回归，仅是与线性回归公式很像，实际上做的是回归后的预测值分类问题

注：sklearn中调用LogisticsRegression这个函数，返回值coef_就是这里的 $\omega$

第二部分 Logistics回归公式推导

上面介绍了Logistics回归的本质就是：线性模型+sigmoid函数（非线性映射），只是说了这样可以拟合出指数级别y的变化。而为何Logistics回归是这种组合，以及如何利用样本去训练二分类模型却没有说明。

需要推导的公式：

$\varPhi = \frac{1}{1+e^{-w^Tx}}\\$

需要得到的模型：w

$\mathop{\arg\min}_{w} \sum_{i=1}^N[y_ilogp(y=1|x)+(1-y_i)logP(y=0|x)]$

第一个公式推导怎么来的？

简单的解释，就是不需要解释这个公式怎么来的，只需要了解经过Sigmoid函数输出值的含义。Sigmoid的输出具有自然的概率属性，它可以将实数集映射到（0,1）的范围。且离1越近，则代表被分类为+1的概率也就越大（概率属性）。让样本下各自标签出现的概率最大【即，监督学习】，这就是Logsitic回归模型的基本想法。
复杂的解释，需要从广义线性模型中推导出来的。

要了解广义线性模型必须先要知道两个概念。指数族分布以及需要满足的三条假设。

知识点一：指数族分布律

需满足以下分布律才可以称为指数族：

$p(y;\eta) = b(y)exp({\eta^TT(y)-a(\eta)})$

其中 $a(\eta)$ 是配分函数，使得分布律最大为1， $\eta$ 是该分布的自然参数， $T(y)$ 是充分统计量。

说明1：`伯努利分布`是指数族分布

伯努利分布(Bernoulli distribution)又名两点分布或0-1分布，介绍伯努利分布前首先需要引入伯努利试验（Bernoulli trial）。

伯努利试验是只有两种可能结果的单次随机试验，即对于一个随机变量X而言：

$\begin{aligned} P_r[X=1]={} &p\\ P_r[X=0]={} &1-p \end{aligned}$

伯努利试验都可以表达为“是或否”的问题。例如，抛一次硬币是正面向上吗？刚出生的小孩是个女孩吗？等等

如果试验E是一个伯努利试验，将E独立重复地进行n次，则称这一串重复的独立试验为n重伯努利试验。
进行一次伯努利试验，成功(X=1)概率为p(0<=p<=1)，失败(X=0)概率为1-p，则称随机变量X服从伯努利分布。伯努利分布是离散型概率分布，其概率质量函数为：

$f\left( x \right) =p^x\left( 1-p \right) ^{1-x}=\left\{ \begin{array}{l} p\\ 1-p\\ 0\\ \end{array}\begin{array}{c} x=1\\ x=0\\ \text{其他}\\ \end{array} \right.$

故根据上述伯努利分布的定义则有：

$\begin{aligned} p(y)={} & \varPhi^y(1-\varPhi )^{1-y}\\ ={} & exp(ln(\varPhi^y(1-\varPhi )^{1-y}))\\ ={} & exp(y\cdot ln(\frac{\varPhi}{1-\varPhi})+ln(1-\varPhi)) \end{aligned}$

与指数族的定义比对： $p(y;\eta) = b(y)exp({\eta^TT(y)-a(\eta)})$

得伯努利确实是指数分布：

$\begin{aligned} b(y) ={} & 1\\ T(y) ={} & y\\ \eta ={} & ln(\frac{\varPhi}{1-\varPhi})\\ a(\eta) ={} & -ln(1-\varPhi) = ln(1+e^\eta) \end{aligned}$

知识点二：广义线性模型需要的三条假设

给定x，y需服从于指数族分布（以满足）
给定x，训练后的模型等于充分统计量的期望： $h(x)=E[T(y|x)]$
自然参数 $\eta$ ，需和观测变量x呈线性关系： $\eta=w^Tx$

根据第一条，伯努利分布是成功(X=1)概率为p，失败(X=0)概率为1-p。对于本例中二分类问题的标签分别为0/1，若设置1的概率为p，0的概率为1-p，很明显看得出标签为0,1分布的二分类问题就是典型的伯努利分布。

根据第二条：

$\begin{aligned} h(x)={} & E[T(y|x)]\\ ={} &E[y|x]=1\times p(y=1)+0\times p(y=0)=p(y=1)=\varPhi \end{aligned}$

又：

$\eta = ln(\frac{\varPhi}{1-\varPhi}) \Rightarrow \varPhi=\frac{1}{1+e^{-\eta}}$

根据第三条： $\eta=w^Tx$ 代入上式

综上：

$\varPhi = \frac{1}{1+e^{-w^Tx}}$

第二公式：模型是怎么训练的？

核心可以总结为下面的公式：

$(min)MLE \Leftrightarrow (min)Loss\ function[Cross Entropy]$

训练模型从优化的角度需要提出个损失函数，让这个损失函数最小。同样的也可以从模型生成的角度出发，让标签出现的概率最大。所以上述的这个公式很好的展现了模型如何训练才可被得到。

这里从模型生成的角度出发来解释问题，首先要提出 $p(y|x;w)$ 的表达式，有两种表达式见下分析。

标签y的分布律为:

在此之前明确的是：

$y$ 是离散值，只有 $\{0,1\}$ 两个标签
$sigmoid$ 输出的是标签的概率，是 $(0,1)$ 之间的连续值。

一开始很不理解： $y(y=1|x)=\sigma(w^Tx)=\frac{1}{1+e^{-w^Tx}}$ 以及 $y(y=0|x)=\sigma(w^Tx)=\frac{e^{-w^Tx}}{1+e^{-w^Tx}}$ 这两个公式，其实很好理解 $\sigma(z)$ 的输出假设为0.1,…,0.6,0.9。输出的值越大，离1越近，则被分为1的概率越大。所以自然而然地将 $（y=1）$ 的概率视为 $\sigma(w^Tx)$ 。【即，也就是之前说的概率属性的含义】

西瓜书版:

$P(y|x;\beta)=y\cdot P(y=1|x;\beta)+(1-y)\cdot P(y=0|x;\beta)$

吴恩达讲课版：

$P(y|x;\beta)=[P(y=1|x;\beta)]^y\cdot[P(y=0|x;\beta)]^{1-y}$

注1：西瓜书和吴恩达对上面两个公式的融合的手段不一样，但是最后可以发现上述两个式子，很好的整合了 $y=1$ 和 $y=0$ 两种情况，自己代入检验一下。

注2：周志华版西瓜书中的公式推导太复杂，吴恩达版公式非常好推，也是经常见到的推导过程。

无论采用上面哪儿一个概率表达式，最后都可以利用极大似然概率估计【MLE】推出w的：

$\begin{aligned} \mathop{\arg\max}_{w}log p(y|x)={} &\mathop{\arg\max}_{w}\sum_{i=1}^{N}log p(y_i|x_i) \\ ={} &\mathop{\arg\max}_{w} \sum_{i=1}^N[y_ilogp(y=1|x)+(1-y_i)logP(y=0|x)]\\ ={} & \mathop{\arg\min}_{w}-(\sum_{i=1}^N[y_ilogp(y=1|x)+(1-y_i)logP(y=0|x)])=\mathop{\arg\min}_{w}Cross\ Entropy \end{aligned}$

总结：

极大似然估计就是找到能让 $y$ 观测变量出现概率最大的模型参数 $\beta$ 【即 $w$ 】
Logistics回归的模型参数的方法有两个：最大化样本出现的概率和最小化交叉熵。两个方法分别是从两种角度建模，模型生成角度和优化角度。

⭐️注3：这里的 $p(y_i|x_i)$ 只是形式上的表达，并非代表条件概率，真正的条件概率实为 $p(y_i|w)$ 。因为已知 $x_i$ 必然已知 $y_i$ ，推导过程中也没有用到贝叶斯公式，算是之前理解的一个坑把。

额外知识点：sigmoid函数的求导（自证）

易证：其中单引号表示对x求导

$\sigma(z)’=\sigma(z)(1-\sigma(z))$

第一部分 对Logistics的概念理解