这是日常学习笔记,转载自https://www.cnblogs.com/jasonfreak/p/5657196.html。原文写的已经足够好,我这里边拷贝边学习,对优质博文进行整理。每篇文章只有20%的干货,对于已经懂了的基础知识进行删减,以达到自我高效吸收的作用
前言
sklearn提供了sklearn.ensemble库,支持众多集成学习算法和模型。恐怕大多数人使用这些工具时,要么使用默认参数,要么根据模型在测试集上的性能试探性地进行调参(当然,完全不懂的参数还是不动算了),要么将调参的工作丢给调参算法(网格搜索等)。这样并不能真正地称为“会”用sklearn进行集成学习。
我认为,学会调参是进行集成学习工作的前提。然而,第一次遇到这些算法和模型时,肯定会被其丰富的参数所吓到,要知道,教材上教的伪代码可没这么多参数啊!!!没关系,暂时,我们只要记住一句话:参数可分为两种,一种是影响模型在训练集上的准确度或影响防止过拟合能力的参数;另一种不影响这两者的其他参数。模型在样本总体上的准确度(后简称准确度)由其在训练集上的准确度及其防止过拟合的能力所共同决定,所以在调参时,我们主要对第一种参数进行调整,最终达到的效果是:模型在训练集上的准确度和防止过拟合能力的大和谐!
本篇博文将详细阐述模型参数背后的理论知识,在下篇博文中,我们将对最热门的两个模型Random Forrest和Gradient Tree Boosting(含分类和回归,所以共4个模型)进行具体的参数讲解。如果你实在无法静下心来学习理论,你也可以在下篇博文中找到最直接的调参指导,虽然我不赞同这么做。
集成学习是什么?
目前,有三种常见的集成学习框架:bagging,boosting和stacking。国内,南京大学的周志华教授对集成学习有很深入的研究,其在09年发表的一篇概述性论文《Ensemble Learning》对这三种集成学习框架有了明确的定义,概括如下:
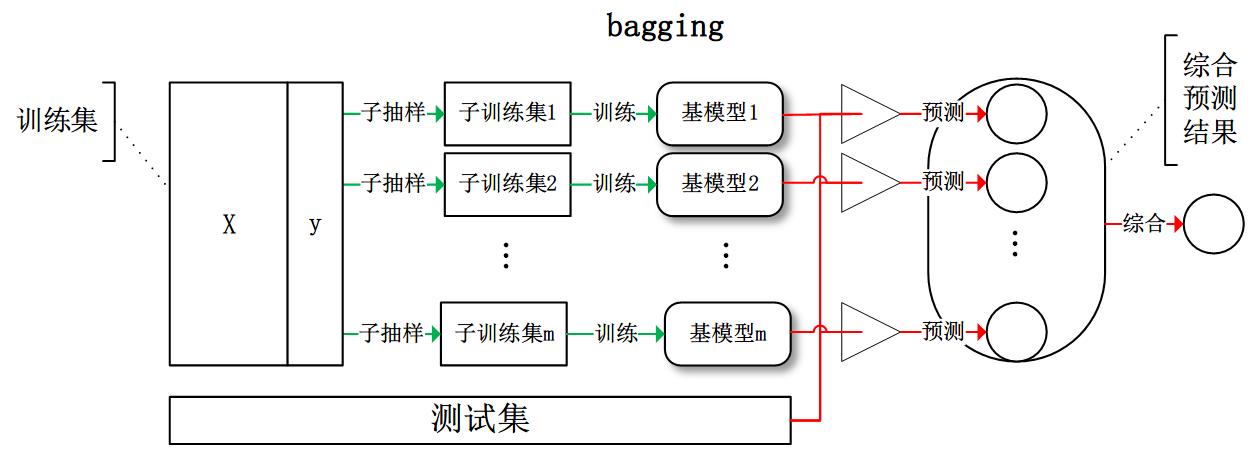
- bagging:从训练集从进行子抽样组成每个基模型所需要的子训练集,对所有基模型预测的结果进行综合产生最终的预测结果:
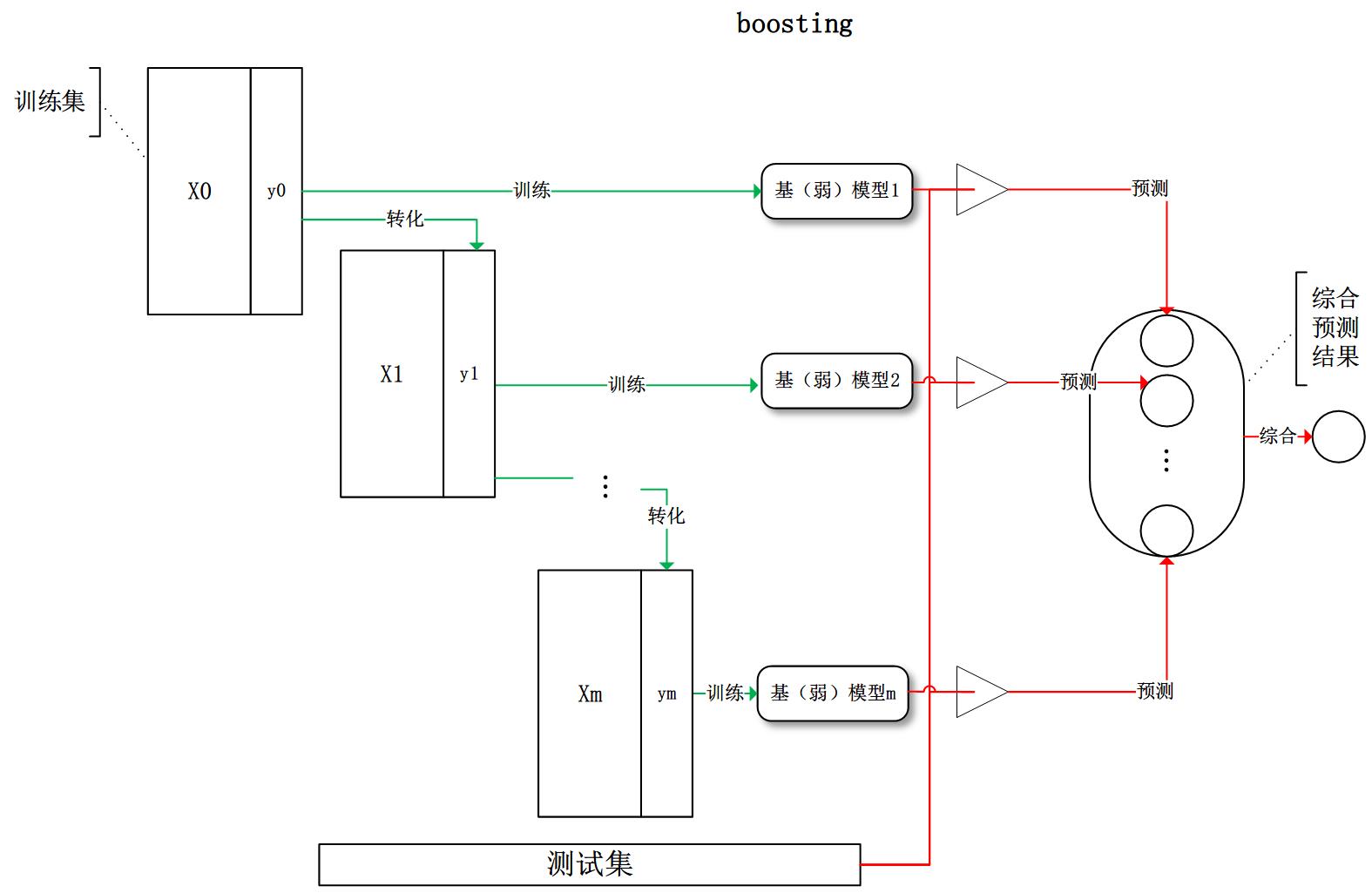
- boosting:训练过程为阶梯状,基模型按次序一一进行训练(
实现上可以做到并行?),基模型的训练集按照某种策略每次都进行一定的转化。对所有基模型预测的结果进行线性综合产生最终的预测结果:
- stacking:将训练好的所有基模型对训练基进行预测,第j个基模型对第i个训练样本的预测值将作为新的训练集中第i个样本的第j个特征值,最后基于新的训练集进行训练。同理,预测的过程也要先经过所有基模型的预测形成新的测试集,最后再对测试集进行预测:

有了这些基本概念之后,直觉将告诉我们,由于不再是单一的模型进行预测,所以模型有了"集思广益"的能力,也就不容易产生过拟合现象。但是,直觉是不可靠的,接下来我们将从模型的偏差和方差入手,彻底搞清楚这一问题。
偏差和方差
样本(广义)的偏差和方差
广义的偏差(bias)描述的是预测值和真实值之间的差异,方差(variance)描述距的是预测值作为随机变量的离散程度。《Understanding the Bias-Variance Tradeoff》当中有一副图形象地向我们展示了偏差和方差的关系

模型的偏差和方差
讨论模型的方差和偏差,需要首先理解到模型也是个随机变量。
原因: 抽样的随机性带来了模型的随机性。如设样本容量为n的训练集为随机变量的集合,那么模型是以这些随机变量为输入的随机变量函数(其本身仍然是随机变量):。
怎么理解这种随机性?对于样本的随机随机性很好理解,直接就是各样本间的差值。模型的随机性可以理解为模型的结构差异。 例如:线性模型中权值向量的差异,树模型中树的结构差异等。在研究模型方差的问题上,我们并不需要对方差进行定量计算,只需要知道其概念即可。
词汇使用场景:方差越大的模型越容易过拟合 ,偏差大说明模型在训练集上的准确度越小
我们常说集成学习框架中的基模型是弱模型,通常来说弱模型是偏差高(在训练集上准确度低)方差小(防止过拟合能力强)的模型。但是,并不是所有集成学习框架中的基模型都是弱模型。bagging和stacking中的基模型为强模型(偏差低方差高),boosting中的基模型为弱模型。
在bagging和boosting框架中, 由于基模型都是线性组成的,通过计算基模型的期望和方差,我们可以得到模型整体的期望和方差。 为了简化模型,我们假设基模型的权重、方差及两两间的相关系数相等。?
